Identric mean
Encyclopedia
The identric mean of two positive real number
s x, y is defined as: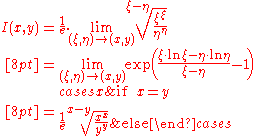
It can be derived from the mean value theorem
by considering the secant of the graph of the function
. It can be generalized to more variables according by the mean value theorem for divided differences. The identric mean is a special case of the Stolarsky mean.
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s x, y is defined as:
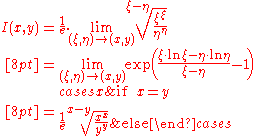
It can be derived from the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
by considering the secant of the graph of the function
. It can be generalized to more variables according by the mean value theorem for divided differences. The identric mean is a special case of the Stolarsky mean.