Stochastic dominance
Encyclopedia
Stochastic dominance is a form of stochastic ordering
. The term is used in decision theory
and decision analysis
to refer to situations where one gamble (a probability distribution
over possible outcomes, also known as prospects) can be ranked as superior to another gamble. It is based on preference
s regarding outcomes. A preference might be a simple ranking of outcomes from favorite to least favored, or it might also employ a value measure (i.e., a number associated with each outcome that allows comparison of multiples of one outcome with another, such as two instances of winning a dollar vs. one instance of winning two dollars.) Only limited knowledge of preferences is required for determining dominance. Risk aversion
is a factor only in second order stochastic dominance.
Stochastic dominance does not give a complete ordering
: For some pairs of gambles, neither one stochastically dominates the other.
A related concept not included under stochastic dominance is deterministic dominance, which occurs when the least preferable outcome of gamble A is more valuable than the most highly preferred outcome of gamble B.
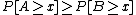for all x, and for some x, 
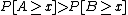. In terms of the cumulative distribution function
s of the two gambles, A dominating B means that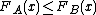
for all x, with strict inequality at some x. For example, consider a die-toss where 1 through 3 wins $1 and 4 through 6 wins $2 in gamble B. This is dominated by a gamble A that yields $3 for 4 through 6 and $1 for 1 through 3, and it is also dominated by a gamble C that gives $2 for 3 through 6 and $1 for 1 and 2. Gamble A would have statewise dominance over B if we re-ordered the die toss outcome by value won, but gamble C has first-order stochastic dominance over B without statewise dominance no matter how we order the prospects
. Further, although when A dominates B, the expected value of the payoff under A will be greater than the expected value of the payoff under B, this is not a sufficient condition for dominance, and so one cannot order lotteries with regard to stochastic dominance simply by comparing the means of their probability distributions.
Every expected utility
maximizer with an increasing utility function
will prefer gamble A over gamble B if A first-order stochastically dominates B.
First-order stochastic dominance can also be expressed as follows: If and only if A first-order stochastically dominates B, there exists some gamble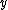
such that 
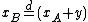where 
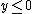in all possible states (and strictly negative in at least one state); here 
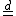means "is equal in distribution to" (that is, "has the same distribution as"). Thus, we can go from the graphed density function of A to that of B by, roughly speaking, pushing some of the probability mass to the left.
expected-utility maximizers
(that is, those with increasing and concave utility functions) prefer a second-order stochastically dominant gamble to a dominated gamble. The same is true for non-expected utility maximizers with utility functions that are locally concave.
In terms of cumulative distribution functions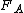
and 
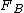, A is second-order stochastically dominant over B if and only if the area under 
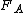from minus infinity to 
is less than or equal to that under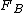 
from minus infinity to 
for all real numbers 
, with strict inequality at some 
; that is,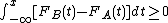 
for all 
, with strict inequality at some 
. Equivalently, 
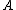dominates 
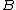in the second order if and only if 
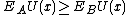for all nondecreasing and concave utility functions 
.
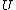Second-order stochastic dominance can also be expressed as follows: If and only if A second-order stochastically dominates B, there exist some gambles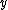
and 
such that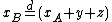 
, with 
always less than or equal to zero, and with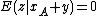 
for all values of 
. Here the introduction of random variable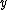 
makes B first-order stochastically dominated by A (making B disliked by those with an increasing utility function), and the introduction of random variable 
introduces a mean-preserving spread
in B which is disliked by those with concave utility. Note that if A and B have the same mean (so that the random variable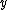
degenerates to the fixed number 0), then B is a mean-preserving spread of A.
and marginal conditional stochastic dominance
.
and 
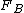be the cumulative distribution functions of two distinct investments 
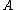and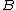 
. 
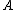dominates 
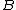in the third order if and only if
and there is at least one strict inequality. Equivalently,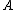
dominates 
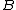in the third order if and only if 
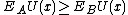for all nondecreasing, concave utility functions 
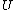that are positively skewed (that is, have a positive third derivative throughout).
Stochastic ordering
In probability theory and statistics, a stochastic order quantifies the concept of one random variable being "bigger" than another. These are usually partial orders, so that one random variable A may be neither stochastically greater than, less than nor equal to another random variable B...
. The term is used in decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
and decision analysis
Decision analysis
Decision analysis is the discipline comprising the philosophy, theory, methodology, and professional practice necessary to address important decisions in a formal manner...
to refer to situations where one gamble (a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
over possible outcomes, also known as prospects) can be ranked as superior to another gamble. It is based on preference
Preference
-Definitions in different disciplines:The term “preferences” is used in a variety of related, but not identical, ways in the scientific literature. This makes it necessary to make explicit the sense in which the term is used in different social sciences....
s regarding outcomes. A preference might be a simple ranking of outcomes from favorite to least favored, or it might also employ a value measure (i.e., a number associated with each outcome that allows comparison of multiples of one outcome with another, such as two instances of winning a dollar vs. one instance of winning two dollars.) Only limited knowledge of preferences is required for determining dominance. Risk aversion
Risk aversion
Risk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....
is a factor only in second order stochastic dominance.
Stochastic dominance does not give a complete ordering
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
: For some pairs of gambles, neither one stochastically dominates the other.
A related concept not included under stochastic dominance is deterministic dominance, which occurs when the least preferable outcome of gamble A is more valuable than the most highly preferred outcome of gamble B.
Statewise dominance
The simplest case of stochastic dominance is statewise dominance (also known as state-by-state dominance), defined as follows: gamble A is statewise dominant over gamble B if A gives a better outcome than B in every possible future state (more precisely, at least as good an outcome in every state, with strict inequality in at least one state). For example, if a dollar is added to one or more prizes in a lottery, the new lottery statewise dominates the old one. Similarly, if a risk insurance policy has a lower premium and a better coverage than another policy, then with or without damage, the outcome is better. Anyone who prefers more to less (in the standard terminology, anyone who has monotonically increasing preferences) will always prefer a statewise dominant gamble.First-order stochastic dominance
Statewise dominance is a special case of the canonical first-order stochastic dominance, defined as follows: gamble A has first-order stochastic dominance over gamble B if for any outcome x, A gives at least as high a probability of receiving at least x as does B, and for some x, A gives a higher probability of receiving at least x. In notation form,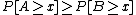 for all x, and for some x, 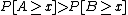. In terms of the cumulative distribution functionCumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s of the two gambles, A dominating B means that
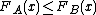for all x, with strict inequality at some x. For example, consider a die-toss where 1 through 3 wins $1 and 4 through 6 wins $2 in gamble B. This is dominated by a gamble A that yields $3 for 4 through 6 and $1 for 1 through 3, and it is also dominated by a gamble C that gives $2 for 3 through 6 and $1 for 1 and 2. Gamble A would have statewise dominance over B if we re-ordered the die toss outcome by value won, but gamble C has first-order stochastic dominance over B without statewise dominance no matter how we order the prospects . Further, although when A dominates B, the expected value of the payoff under A will be greater than the expected value of the payoff under B, this is not a sufficient condition for dominance, and so one cannot order lotteries with regard to stochastic dominance simply by comparing the means of their probability distributions.
Every expected utility
Expected utility hypothesis
In economics, game theory, and decision theory the expected utility hypothesis is a theory of utility in which "betting preferences" of people with regard to uncertain outcomes are represented by a function of the payouts , the probabilities of occurrence, risk aversion, and the different utility...
maximizer with an increasing utility function
Utility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
will prefer gamble A over gamble B if A first-order stochastically dominates B.
First-order stochastic dominance can also be expressed as follows: If and only if A first-order stochastically dominates B, there exists some gamble
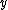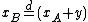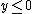such that where in all possible states (and strictly negative in at least one state); here 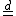means "is equal in distribution to" (that is, "has the same distribution as"). Thus, we can go from the graphed density function of A to that of B by, roughly speaking, pushing some of the probability mass to the left.Second-order stochastic dominance
The other commonly used type of stochastic dominance is second-order stochastic dominance. Roughly speaking, for two gambles A and B, gamble A has second-order stochastic dominance over gamble B if the former is more predictable (i.e. involves less risk) and has at least as high a mean. All risk-averseRisk aversion
Risk aversion is a concept in psychology, economics, and finance, based on the behavior of humans while exposed to uncertainty....
expected-utility maximizers
Expected utility hypothesis
In economics, game theory, and decision theory the expected utility hypothesis is a theory of utility in which "betting preferences" of people with regard to uncertain outcomes are represented by a function of the payouts , the probabilities of occurrence, risk aversion, and the different utility...
(that is, those with increasing and concave utility functions) prefer a second-order stochastically dominant gamble to a dominated gamble. The same is true for non-expected utility maximizers with utility functions that are locally concave.
In terms of cumulative distribution functions
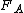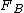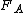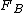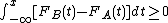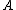and , A is second-order stochastically dominant over B if and only if the area under from minus infinity to is less than or equal to that under from minus infinity to for all real numbers , with strict inequality at some ; that is, for all , with strict inequality at some . Equivalently, dominates 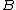in the second order if and only if 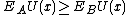for all nondecreasing and concave utility functions 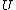.Second-order stochastic dominance can also be expressed as follows: If and only if A second-order stochastically dominates B, there exist some gambles
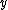and such that 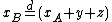, with always less than or equal to zero, and with 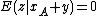for all values of . Here the introduction of random variable 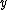makes B first-order stochastically dominated by A (making B disliked by those with an increasing utility function), and the introduction of random variable introduces a mean-preserving spreadMean-preserving spread
In probability and statistics, a mean-preserving spread is a change from one probability distribution A to another probability distribution B, where B is formed by spreading out one or more portions of A's probability density function while leaving the mean unchanged...
in B which is disliked by those with concave utility. Note that if A and B have the same mean (so that the random variable
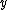degenerates to the fixed number 0), then B is a mean-preserving spread of A.Second-order stochastic dominance in portfolio analysis
Portfolio analysis typically assumes that all investors are risk averse. Therefore, no investor would choose a portfolio that is second-order stochastically dominated by some other portfolio. See modern portfolio theoryModern portfolio theory
Modern portfolio theory is a theory of investment which attempts to maximize portfolio expected return for a given amount of portfolio risk, or equivalently minimize risk for a given level of expected return, by carefully choosing the proportions of various assets...
and marginal conditional stochastic dominance
Marginal conditional stochastic dominance
In finance, marginal conditional stochastic dominance is a condition under which a portfolio can be improved in the eyes of all risk-averse investors by incrementally moving funds out of one asset and into another...
.
Sufficient conditions for second-order stochastic dominance
- First-order stochastic dominance is a sufficient condition.
Necessary conditions for second-order stochastic dominance
-
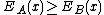is a necessary condition. - If
dominates 
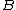in the second order, then the geometric mean of 
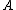must be greater than or equal to the geometric mean of 
. -
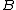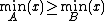is a necessary condition. The condition implies that the left tail of 
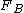must be thicker than the left tail of 
.
Third-order stochastic dominance
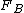Let and be the cumulative distribution functions of two distinct investments 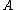and 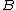. 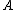dominates 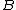in the third order if and only if-
for all 
,
-
,
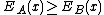and there is at least one strict inequality. Equivalently,
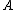dominates 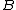in the third order if and only if 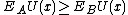for all nondecreasing, concave utility functions 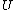that are positively skewed (that is, have a positive third derivative throughout).Sufficient condition for third-order stochastic dominance
- Second-order stochastic dominance is a sufficient condition.
Necessary conditions for third-order stochastic dominance
-
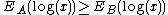is a necessary condition. The condition implies that the geometric mean of 
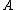must be greater than or equal to the geometric mean of 
. -
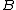is a necessary condition. The condition implies that the left tail of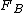 
must be thicker than the left tail of 
.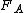