Stochastic ordering
Encyclopedia
In probability theory
and statistics
, a stochastic order quantifies the concept of one random variable
being "bigger" than another. These are usually partial orders, so that one random variable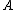
may be neither stochastically greater than, less than nor equal to another random variable 
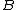. Many different orders exist, which have different applications.
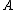is less than a random variable 
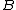in the "usual stochastic order" if
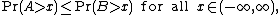
where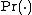
denotes the probability of an event.
This is sometimes denoted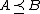
or 
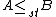. If additionally 
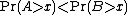for some 
, then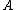 
is stochastically strictly less than 
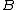, sometimes denoted 
.
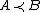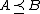and 
then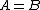 
in distribution.
is a stochastic ordering used in decision theory
. Several "orders" of stochastic dominance are defined.
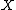with absolutely continuous distribution function 
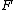and density function 
is defined as
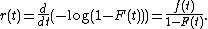
Given two non-negative variables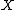
and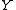 
with absolutely continuous distribution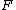
and 
,
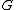and with hazard rate functions
and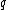 
, respectively,
is said to be smaller than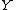 
in the hazard rate order
(denoted as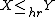
) if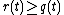
for all 
,
or equivalently if
is decreasing in 
.
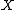and 
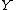two continuous (or discrete) random variables with densities (or discrete densities) 
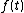and 
, respectively, so that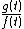 
increases in 
over the union of the supports of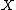 
and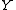 
; in this case, 
is smaller than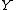 
in the likelihood ratio order (
).
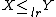, but more fully by a range of stochastic orders.
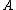is less than 
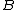if and only if for all convex 
, 
.
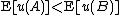is an exponential function: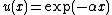 
. Clearly, two random variables that are convex ordered are also Laplace transform ordered. The converse is not true.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a stochastic order quantifies the concept of one random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
being "bigger" than another. These are usually partial orders, so that one random variable
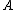may be neither stochastically greater than, less than nor equal to another random variable 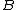. Many different orders exist, which have different applications.Usual stochastic order
A real random variable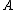 is less than a random variable 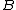in the "usual stochastic order" if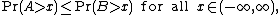where
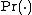denotes the probability of an event.This is sometimes denoted
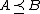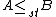or . If additionally 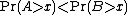for some , then 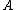is stochastically strictly less than 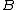, sometimes denoted 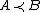.Characterizations
The following rules describe cases when one random variable is stochastically less than or equal to another. Strict version of some of these rules also exist.
if and only if for all non-decreasing functions 
, 
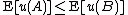.- If
is non-decreasing and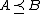 
then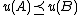 
- If
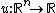is an increasing function 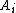and 
and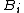 
are independent sets of random variables with 
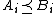for each 
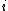, then 
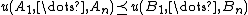and in particular 
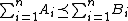Moreover, the 
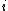th order statisticOrder statisticIn statistics, the kth order statistic of a statistical sample is equal to its kth-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference....
s satisfy
. - If two sequences of random variables
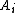and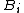 
, with 
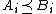for all 
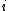each converge in distribution, then their limits satisfy 
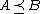. - If
, 
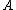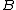and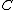 
are random variables such that 
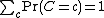and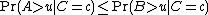 
for all 
and 
such that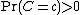 
, then 
.
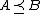Other properties
If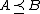 and then 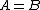in distribution.Stochastic dominance
Stochastic dominanceStochastic dominance
Stochastic dominance is a form of stochastic ordering. The term is used in decision theory and decision analysis to refer to situations where one gamble can be ranked as superior to another gamble. It is based on preferences regarding outcomes...
is a stochastic ordering used in decision theory
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
. Several "orders" of stochastic dominance are defined.
- Zeroth order stochastic dominance consists of simple inequality:
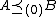if 
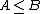for all states of natureState of natureState of nature is a term in political philosophy used in social contract theories to describe the hypothetical condition that preceded governments...
. - First order stochastic dominance is equivalent to the usual stochastic order above.
- Higher order stochastic dominance is defined in terms of integrals of the distribution functionDistribution functionIn molecular kinetic theory in physics, a particle's distribution function is a function of seven variables, f, which gives the number of particles per unit volume in phase space. It is the number of particles per unit volume having approximately the velocity near the place and time...
. - Lower order stochastic dominance implies higher order stochastic dominance.
Hazard rate order
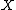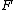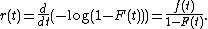
The hazard rate of a non-negative random variable with absolutely continuous distribution function and density function is defined asGiven two non-negative variables
and 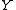with absolutely continuous distribution
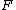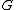and ,and with hazard rate functions
and 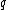, respectively, is said to be smaller than 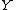in the hazard rate order(denoted as
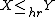) if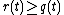 for all ,or equivalently if
is decreasing in .Likelihood ratio order
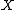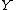Let and two continuous (or discrete) random variables with densities (or discrete densities) 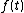and , respectively, so that 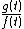increases in over the union of the supports of 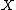and 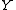; in this case, is smaller than 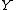in the likelihood ratio order (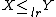).Variability orders
If two variables have the same mean, they can still be compared by how "spread out" their distributions are. This is captured to a limited extent by the varianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, but more fully by a range of stochastic orders.
Convex order
Convex order is a special kind of variability order. Under the convex ordering,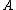 is less than 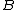if and only if for all convex , 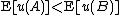.Laplace transform order
Laplace transform order is a special case of convex order where is an exponential function: 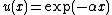. Clearly, two random variables that are convex ordered are also Laplace transform ordered. The converse is not true.