
Pappus chain
Encyclopedia
In geometry
, the Pappus chain was created by Pappus of Alexandria
in the 3rd century AD.
is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV. Let the radii of these two circles be denoted as rU and rV, respectively, and let their respective centers be the points U and V. The Pappus chain consists of the circles in the shaded grey region, which are externally tangent to CU (the inner circle) and internally tangent to CV (the outer circle). Let the radius, diameter and center point of the nth circle of the Pappus chain be denoted as rn, dn and Pn, respectively.
, for the following reason. The sum of the distances from the nth circle of the Pappus chain to the two centers U and V of the arbelos circles equals a constant
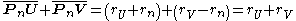
Thus, the foci
of this ellipse are U and V, the centers of the two circles that define the arbelos; these points correspond to the midpoints of the line segments AB and AC, respectively.


The same inversion can be used to show that the points where the circles of the Pappus chain are tangent to one another lie on a common circle. As noted above, the inversion centered at point A transforms the arbelos circles CU and CV into two parallel lines, and the circles of the Pappus chain into a stack of equally sized circles sandwiched between the two parallel lines. Hence, the points of tangency between the transformed circles lie on a line midway between the two parallel lines. Undoing the inversion in the circle, this line of tangent points is transformed back into a circle.
, in which finitely many circles are tangent to two circles.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the Pappus chain was created by Pappus of Alexandria
Pappus of Alexandria
Pappus of Alexandria was one of the last great Greek mathematicians of Antiquity, known for his Synagoge or Collection , and for Pappus's Theorem in projective geometry...
in the 3rd century AD.
Construction
The arbelosArbelos
In geometry, an arbelos is a plane region bounded by a semicircle of diameter 1, connected to semicircles of diameters r and , all oriented the same way and sharing a common baseline. Archimedes is believed to be the first mathematician to study its mathematical properties, as it appears in...
is defined by two circles, CU and CV, which are tangent at the point A and where CU is enclosed by CV. Let the radii of these two circles be denoted as rU and rV, respectively, and let their respective centers be the points U and V. The Pappus chain consists of the circles in the shaded grey region, which are externally tangent to CU (the inner circle) and internally tangent to CV (the outer circle). Let the radius, diameter and center point of the nth circle of the Pappus chain be denoted as rn, dn and Pn, respectively.
Ellipse
All the centers of the circles in the Pappus chain are located on a common ellipseEllipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, for the following reason. The sum of the distances from the nth circle of the Pappus chain to the two centers U and V of the arbelos circles equals a constant
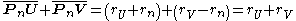
Thus, the foci
Focus (geometry)
In geometry, the foci are a pair of special points with reference to which any of a variety of curves is constructed. For example, foci can be used in defining conic sections, the four types of which are the circle, ellipse, parabola, and hyperbola...
of this ellipse are U and V, the centers of the two circles that define the arbelos; these points correspond to the midpoints of the line segments AB and AC, respectively.
Coordinates
If r = AC/AB, then the center of the nth circle in the chain is:
Radii of the circles
If r = AC/AB, then the radius of the nth circle in the chain is:
Circle inversion
The height hn of the center of the nth circle above the base diameter ACB equals n times dn. This may be shown by inverting in a circle centered on the tangent point A. The circle of inversion is chosen to intersect the nth circle perpendicularly, so that the nth circle is transformed into itself. The two arbelos circles, CU and CV, are transformed into parallel lines tangent to and sandwiching the nth circle; hence, the other circles of the Pappus chain are transformed into similarly sandwiched circles of the same diameter. The initial circle C0 and the final circle Cn each contribute ½dn to the height hn, whereas the circles C1–Cn−1 each contribute dn. Adding these contributions together yields the equation hn = n dn.The same inversion can be used to show that the points where the circles of the Pappus chain are tangent to one another lie on a common circle. As noted above, the inversion centered at point A transforms the arbelos circles CU and CV into two parallel lines, and the circles of the Pappus chain into a stack of equally sized circles sandwiched between the two parallel lines. Hence, the points of tangency between the transformed circles lie on a line midway between the two parallel lines. Undoing the inversion in the circle, this line of tangent points is transformed back into a circle.
Steiner chain
In these properties of having centers on an ellipse and tangencies on a circle, the Pappus chain is analogous to the Steiner chainSteiner chain
In geometry, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles , where n is finite and each circle in the chain is tangent to the previous and next circles in the chain...
, in which finitely many circles are tangent to two circles.

