
Subindependence
Encyclopedia
In probability theory
and statistics
, subindependence is a weak form of independence.
Two random variable
s X and Y are said to be subindependent if the characteristic function of their sum is equal to the product of their marginal characteristic functions. Symbolically:
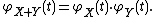
This is a generalization of the concept of independence of random variables, i.e. if two random variables are independent then they are subindependent, but not conversely. If two random variables are subindependent, and if their covariance exists, then they are uncorrelated
.
Subindependence has some peculiar properties: for example, there exist random variables X and Y that are subindependent, but X and αY are not subindependent when α ≠ 1.
There is at least one example case of a joint distribution where the variables are subindependent, but not independent.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, subindependence is a weak form of independence.
Two random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s X and Y are said to be subindependent if the characteristic function of their sum is equal to the product of their marginal characteristic functions. Symbolically:
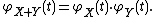
This is a generalization of the concept of independence of random variables, i.e. if two random variables are independent then they are subindependent, but not conversely. If two random variables are subindependent, and if their covariance exists, then they are uncorrelated
Uncorrelated
In probability theory and statistics, two real-valued random variables are said to be uncorrelated if their covariance is zero. Uncorrelatedness is by definition pairwise; i.e...
.
Subindependence has some peculiar properties: for example, there exist random variables X and Y that are subindependent, but X and αY are not subindependent when α ≠ 1.
There is at least one example case of a joint distribution where the variables are subindependent, but not independent.

