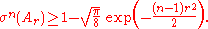Spherical measure
Encyclopedia
In mathematics
— specifically, in geometric measure theory
— spherical measure σn is the “natural” Borel measure on the n-sphere Sn. Spherical measure is often normalized so that it is a probability measure
on the sphere, i.e. so that σn(Sn) = 1.
ρn on Sn; that is, for points x and y in Sn, ρn(x, y) is defined to be the (Euclidean) angle that they subtend at the centre of the sphere (the origin of Rn+1). Now construct n-dimensional Hausdorff measure
Hn on the metric space (Sn, ρn) and define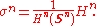
One could also have given Sn the metric that it inherits as a subspace of the Euclidean space Rn+1; the same spherical measure results from this choice of metric.
Another method uses Lebesgue measure
λn+1 on the ambient Euclidean space Rn+1: for any measurable subset A of Sn, define σn(A) to be the (n + 1)-dimensional volume of the “wedge” in the ball Bn+1 that it subtends at the origin. That is,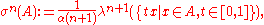
where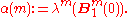
The fact that all these methods define the same measure on Sn follows from an elegant result of Christensen: all these measures are obviously uniformly distributed
on Sn, and any two uniformly distributed Borel regular measures on a separable metric space must be constant (positive) multiples of one another. Since all our candidate σn’s have been normalized to be probability measures, they are all the same measure.
Spherical measure has a nice relationship to Haar measure
on the orthogonal group
. Let O(n) denote the orthogonal group acting
on Rn and let θn denote its normalized Haar measure (so that θn(O(n)) = 1). The orthogonal group also acts on the sphere Sn−1. Then, for any x ∈ Sn−1 and any A ⊆ Sn−1,
In the case that Sn is a topological group
(that is, when n is 0, 1 or 3), spherical measure σn coincides with (normalized) Haar measure on Sn.
If A ⊆ Sn−1 is any Borel set and B⊆ Sn−1 is a ρn-ball with the same σn-measure as A, then, for any r > 0,
where Ar denotes the “inflation” of A by r, i.e.
In particular, if σn(A) ≥ ½ and n ≥ 2, then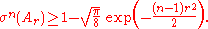
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in geometric measure theory
Geometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
— spherical measure σn is the “natural” Borel measure on the n-sphere Sn. Spherical measure is often normalized so that it is a probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
on the sphere, i.e. so that σn(Sn) = 1.
Definition of spherical measure
There are several ways to define spherical measure. One way is to use the usual “round” or “arclength” metricMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
ρn on Sn; that is, for points x and y in Sn, ρn(x, y) is defined to be the (Euclidean) angle that they subtend at the centre of the sphere (the origin of Rn+1). Now construct n-dimensional Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
Hn on the metric space (Sn, ρn) and define
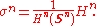
One could also have given Sn the metric that it inherits as a subspace of the Euclidean space Rn+1; the same spherical measure results from this choice of metric.
Another method uses Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
λn+1 on the ambient Euclidean space Rn+1: for any measurable subset A of Sn, define σn(A) to be the (n + 1)-dimensional volume of the “wedge” in the ball Bn+1 that it subtends at the origin. That is,
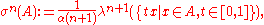
where
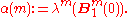
The fact that all these methods define the same measure on Sn follows from an elegant result of Christensen: all these measures are obviously uniformly distributed
Uniformly distributed measure
In mathematics — specifically, in geometric measure theory — a uniformly distributed measure on a metric space is one for which the measure of an open ball depends only on its radius and not on its centre. By convention, the measure is also required to be Borel regular, and to take...
on Sn, and any two uniformly distributed Borel regular measures on a separable metric space must be constant (positive) multiples of one another. Since all our candidate σn’s have been normalized to be probability measures, they are all the same measure.
Relationship with other measures
The relationship of spherical measure to Hausdorff measure on the sphere and Lebesgue measure on the ambient space has already been discussed.Spherical measure has a nice relationship to Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
on the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
. Let O(n) denote the orthogonal group acting
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
on Rn and let θn denote its normalized Haar measure (so that θn(O(n)) = 1). The orthogonal group also acts on the sphere Sn−1. Then, for any x ∈ Sn−1 and any A ⊆ Sn−1,

In the case that Sn is a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
(that is, when n is 0, 1 or 3), spherical measure σn coincides with (normalized) Haar measure on Sn.
Isoperimetric inequality
There is an isoperimetric inequality for the sphere with its usual metric and spherical measure (see Ledoux & Talagrand, chapter 1):If A ⊆ Sn−1 is any Borel set and B⊆ Sn−1 is a ρn-ball with the same σn-measure as A, then, for any r > 0,

where Ar denotes the “inflation” of A by r, i.e.

In particular, if σn(A) ≥ ½ and n ≥ 2, then