
Uniformly distributed measure
Encyclopedia
In mathematics
— specifically, in geometric measure theory
— a uniformly distributed measure on a metric space
is one for which the measure of an open ball depends only on its radius and not on its centre. By convention, the measure is also required to be Borel regular
, and to take positive and finite values on open balls of finite radius. Thus, if (X, d) is a metric space, a Borel regular measure μ on X is said to be uniformly distributed if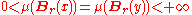
for all points x and y of X and all 0 < r < +∞, where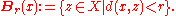
Let μ and ν be uniformly distributed Borel regular measures on a separable metric space (X, d). Then there is a constant c such that μ = cν.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in geometric measure theory
Geometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
— a uniformly distributed measure on a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
is one for which the measure of an open ball depends only on its radius and not on its centre. By convention, the measure is also required to be Borel regular
Borel regular measure
In mathematics, an outer measure μ on n-dimensional Euclidean space Rn is called Borel regular if the following two conditions hold:...
, and to take positive and finite values on open balls of finite radius. Thus, if (X, d) is a metric space, a Borel regular measure μ on X is said to be uniformly distributed if
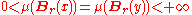
for all points x and y of X and all 0 < r < +∞, where
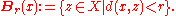
Christensen’s lemma
As it turns out, uniformly distributed measures are very rigid objects. On any “decent” metric space, the uniformly distributed measures form a one-parameter linearly dependent family:Let μ and ν be uniformly distributed Borel regular measures on a separable metric space (X, d). Then there is a constant c such that μ = cν.

