
Spatial analysis
Encyclopedia
Scientific technique
A scientific technique is any systematic way of obtaining information about a scientific nature or to obtain a desired material or product.Scientific techniques can be divided in many different groups, e.g.:# Preparative techniques...
which study entities using their topological, geometric, or geographic properties. The phrase properly refers to a variety of techniques, many still in their early development, using different analytic approaches and applied in fields as diverse as astronomy, with its studies of the placement of galaxies in the cosmos, to chip fabrication engineering, with its use of 'place and route' algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
s to build complex wiring structures. The phrase is often used in a more restricted sense to describe techniques applied to structures at the human scale, most notably in the analysis of geographic data
Data
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
. The phrase is even sometimes used to refer to a specific technique in a single area of research, for example, to describe geostatistics
Geostatistics
Geostatistics is a branch of statistics focusing on spatial or spatiotemporal datasets. Developed originally to predict probability distributions of ore grades for mining operations, it is currently applied in diverse disciplines including petroleum geology, hydrogeology, hydrology, meteorology,...
.
Complex issues arise in spatial analysis, many of which are neither clearly defined nor completely resolved, but form the basis for current research. The most fundamental of these is the problem of defining the spatial location of the entities being studied. For example, a study on human health could describe the spatial position of humans with a point placed where they live, or with a point located where they work, or by using a line to describe their weekly trips; each choice has dramatic effects on the techniques which can be used for the analysis and on the conclusions which can be obtained. Other issues in spatial analysis include the limitations of mathematical knowledge, the assumptions required by existing statistical techniques, and problems in computer based calculations.
Classification of the techniques of spatial analysis is difficult because of the large number of different fields of research involved, the different fundamental approaches which can be chosen, and the many forms the data can take.
The history of spatial analysis
Spatial analysis can perhaps be considered to have arisen with the early attempts at cartographyCartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
and surveying
Surveying
See Also: Public Land Survey SystemSurveying or land surveying is the technique, profession, and science of accurately determining the terrestrial or three-dimensional position of points and the distances and angles between them...
but many fields have contributed to its rise in modern form. Biology
Biology
Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
contributed through botanical
Botany
Botany, plant science, or plant biology is a branch of biology that involves the scientific study of plant life. Traditionally, botany also included the study of fungi, algae and viruses...
studies of global plant distributions and local plant locations, ethological
Ethology
Ethology is the scientific study of animal behavior, and a sub-topic of zoology....
studies of animal movement, landscape ecological
Landscape ecology
Landscape ecology is the science of studying and improving relationships between urban development and ecological processes in the environment and particular ecosystems...
studies of vegetation blocks, ecological
Ecology
Ecology is the scientific study of the relations that living organisms have with respect to each other and their natural environment. Variables of interest to ecologists include the composition, distribution, amount , number, and changing states of organisms within and among ecosystems...
studies of spatial population dynamics, and the study of biogeography
Biogeography
Biogeography is the study of the distribution of species , organisms, and ecosystems in space and through geological time. Organisms and biological communities vary in a highly regular fashion along geographic gradients of latitude, elevation, isolation and habitat area...
. Epidemiology
Epidemiology
Epidemiology is the study of health-event, health-characteristic, or health-determinant patterns in a population. It is the cornerstone method of public health research, and helps inform policy decisions and evidence-based medicine by identifying risk factors for disease and targets for preventive...
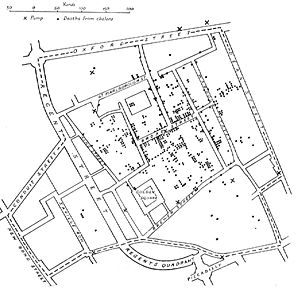
contributed with early work on disease mapping, notably John Snow
John Snow (physician)
John Snow was an English physician and a leader in the adoption of anaesthesia and medical hygiene. He is considered to be one of the fathers of epidemiology, because of his work in tracing the source of a cholera outbreak in Soho, England, in 1854.-Early life and education:Snow was born 15 March...
's work mapping an outbreak of cholera, with research on mapping the spread of disease and with locational studies for health care delivery. Statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
has contributed greatly through work in spatial statistics. Economics
Economics
Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
has contributed notably through spatial econometrics
Spatial econometrics
Spatial Econometrics is the field where spatial analysis and econometrics intersect. In general, econometrics differs from other branches of statistics in focusing on theoretical models, whose parameters are estimated using regression analysis...
. Geographic information system
Geographic Information System
A geographic information system, geographical information science, or geospatial information studies is a system designed to capture, store, manipulate, analyze, manage, and present all types of geographically referenced data...
is currently a major contributor due to the importance of geographic software in the modern analytic toolbox. Remote sensing
Remote sensing
Remote sensing is the acquisition of information about an object or phenomenon, without making physical contact with the object. In modern usage, the term generally refers to the use of aerial sensor technologies to detect and classify objects on Earth by means of propagated signals Remote sensing...
has contributed extensively in morphometric and clustering analysis. Computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
has contributed extensively through the study of algorithms, notably in computational geometry
Computational geometry
Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...
. Mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
continues to provide the fundamental tools for analysis and to reveal the complexity of the spatial realm, for example, with recent work on fractals and scale invariance
Scale invariance
In physics and mathematics, scale invariance is a feature of objects or laws that do not change if scales of length, energy, or other variables, are multiplied by a common factor...
. Scientific modelling
Scientific modelling
Scientific modelling is the process of generating abstract, conceptual, graphical and/or mathematical models. Science offers a growing collection of methods, techniques and theory about all kinds of specialized scientific modelling...
provides a useful framework for new approaches.
Fundamental issues in spatial analysis
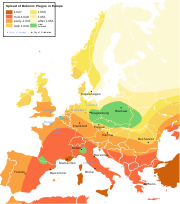
Spatial analysis confronts many fundamental issues in the definition of its objects of study, in the construction of the analytic operations to be used, in the use of computers for analysis, in the limitations and particularities of the analyses which are known, and in the presentation of analytic results. Many of these issues are active subjects of modern research.Common errors often arise in spatial analysis, some due to the mathematics of space, some due to the particular ways data are presented spatially, some due to the tools which are available. Census data, because it protects individual privacy by aggregating data into local units, raises a number of statistical issues. The fractal nature of coastline makes precise measurements of its length difficult if not impossible. A computer software fitting straight lines to the curve of a coastline, can easily calculate the lengths of the lines which it defines. However these straight lines may have no inherent meaning in the real world, as was shown for the coastline of Britain
How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension
"How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension" is a paper by mathematician Benoît Mandelbrot, first published in Science in 1967. In this paper Mandelbrot discusses self-similar curves that have Hausdorff dimension between 1 and 2...
.
These problems represent one of the greatest dangers in spatial analysis because of the inherent power of maps as media of presentation. When results are presented as maps, the presentation combines the spatial data which is generally very accurate with analytic results which may be grossly inaccurate. Some of these issues are discussed at length in the book How to Lie with Maps
Spatial characterization
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
, it is particularly important in spatial analysis because the tools to define and study entities favor specific characterizations of the entities being studied. Statistical techniques favor the spatial definition of objects as points because there are very few statistical techniques which operate directly on line, area, or volume elements. Computer tools favor the spatial definition of objects as homogeneous and separate elements
Atom (measure theory)
In mathematics, more precisely in measure theory, an atom is a measurable set which has positive measure and contains no set of smaller but positive measure...
because of the limited number of database
Database
A database is an organized collection of data for one or more purposes, usually in digital form. The data are typically organized to model relevant aspects of reality , in a way that supports processes requiring this information...
elements and computational structures available, and the ease with which these primitive structures can be created.
Spatial dependency or auto-correlation
Spatial dependency is the co-variation of properties within geographic space: characteristics at proximal locations appear to be correlated, either positively or negatively. Spatial dependency leads to the spatial autocorrelationAutocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
problem in statistics since, like temporal autocorrelation, this violates standard statistical techniques that assume independence among observations. For example, regression
Regression
Regression could refer to:* Regression , a defensive reaction to some unaccepted impulses* Regression analysis, a statistical technique for estimating the relationships among variables...
analyses that do not compensate for spatial dependency can have unstable parameter estimates and yield unreliable significance tests. Spatial regression models (see below) capture these relationships and do not suffer from these weaknesses. It is also appropriate to view spatial dependency as a source of information rather than something to be corrected.
Locational effects also manifest as spatial heterogeneity, or the apparent variation in a process with respect to location in geographic space. Unless a space is uniform and boundless, every location will have some degree of uniqueness relative to the other locations. This affects the spatial dependency relations and therefore the spatial process. Spatial heterogeneity means that overall parameters estimated for the entire system may not adequately describe the process at any given location.
Scaling
Spatial measurementMeasurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
scale is a persistent issue in spatial analysis; more detail is available at the modifiable areal unit problem
Modifiable Areal Unit Problem
The modifiable areal unit problem is a source of statistical bias that can radically affect the results of statistical hypothesis tests. It affects results when point-based measures of spatial phenomena are aggregated into districts. The resulting summary values are influenced by the choice of...
(MAUP) topic entry. Landscape ecologists developed a series of scale invariant metrics for aspects of ecology that are fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
in nature. In more general terms, no scale independent
Objectivity (frame invariance)
The concept of objectivity in science means that qualitative and quantitative descriptions of physical phenomena remain unchanged when the phenomena are observed under a variety of conditions...
method of analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
is widely agreed upon for spatial statistics.
Sampling
Spatial samplingSampling (statistics)
In statistics and survey methodology, sampling is concerned with the selection of a subset of individuals from within a population to estimate characteristics of the whole population....
involves determining a limited number of locations in geographic space for faithfully measuring phenomena that are subject to dependency and heterogeneity. Dependency suggests that since one location can predict the value of another location, we do not need observations in both places. But heterogeneity suggests that this relation can change across space, and therefore we cannot trust an observed degree of dependency beyond a region that may be small. Basic spatial sampling schemes include random, clustered and systematic. These basic schemes can be applied at multiple levels in a designated spatial hierarchy (e.g., urban area, city, neighborhood). It is also possible to exploit ancillary data, for example, using property values as a guide in a spatial sampling scheme to measure educational attainment and income. Spatial models such as autocorrelation statistics, regression and interpolation (see below) can also dictate sample design.
Common errors in spatial analysis
The fundamental issues in spatial analysis lead to numerous problems in analysis including bias, distortion and outright errors in the conclusions reached. These issues are often interlinked but various attempts have been made to separate out particular issues from each other.Length
In a paper by Benoit MandelbrotBenoît Mandelbrot
Benoît B. Mandelbrot was a French American mathematician. Born in Poland, he moved to France with his family when he was a child...
on the coastline of Britain
How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension
"How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension" is a paper by mathematician Benoît Mandelbrot, first published in Science in 1967. In this paper Mandelbrot discusses self-similar curves that have Hausdorff dimension between 1 and 2...
it was shown that it is inherently nonsensical to discuss certain spatial concepts despite an inherent presumption of the validity of the concept. Lengths in ecology depend directly on the scale at which they are measured and experienced. So while surveyors commonly measure the length of a river, this length only has meaning in the context of the relevance of the measuring technique to the question under study.
Locational fallacy
The locational fallacy refers to error due to the particular spatial characterization chosen for the elements of study, in particular choice of placement for the spatial presence of the element.Spatial characterizations may be simplistic or even wrong. Studies of humans often reduce the spatial existence of humans to a single point, for instance their home address. This can easily lead to poor analysis, for example, when considering disease transmission which can happen at work or at school and therefore far from the home.
The spatial characterization may implicitly limit the subject of study. For example, the spatial analysis of crime data has recently become popular but these studies can only describe the particular kinds of crime which can be described spatially. This leads to many maps of assault but not to any maps of embezzlement with political consequences in the conceptualization of crime and the design of policies to address the issue.
Atomic fallacy
This describes errors due to treating elements as separate 'atoms' outside of their spatial context.Ecological fallacy
The ecological fallacyEcological fallacy
An ecological fallacy is a logical fallacy in the interpretation of statistical data in an ecological study, whereby inferences about the nature of specific individuals are based solely upon aggregate statistics collected for the group to which those individuals belong...
describes errors due to performing analyses on aggregate data when trying to reach conclusions on the individual units. Errors occur in part from spatial aggregation. For example a pixel
Pixel
In digital imaging, a pixel, or pel, is a single point in a raster image, or the smallest addressable screen element in a display device; it is the smallest unit of picture that can be represented or controlled....
represents the average surface temperatures within an area. Ecological fallacy would be to assume that all points within the area have the same temperature. This topic is closely related to the modifiable areal unit problem
Modifiable Areal Unit Problem
The modifiable areal unit problem is a source of statistical bias that can radically affect the results of statistical hypothesis tests. It affects results when point-based measures of spatial phenomena are aggregated into districts. The resulting summary values are influenced by the choice of...
.
Geographic space

The Euclidean distance
Euclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
between locations often represents their proximity, although this is only one possibility. There are an infinite number of distances in addition to Euclidean that can support quantitative analysis. For example, "Manhattan" (or "Taxicab
Taxicab geometry
Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...
") distances where movement is restricted to paths parallel to the axes can be more meaningful than Euclidean distances in urban settings. In addition to distances, other geographic relationships such as connectivity (e.g., the existence or degree of shared borders) and direction can also influence the relationships among entities. It is also possible to compute minimal cost paths across a cost surface; for example, this can represent proximity among locations when travel must occur across rugged terrain.
Types of spatial analysis
Spatial data comes in many varieties and it is not easy to
arrive at a system of classification that is simultaneously
exclusive, exhaustive, imaginative, and satisfying.
-- G. Upton & B. Fingelton
Spatial autocorrelation
Spatial autocorrelationAutocorrelation
Autocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
statistics measure and analyze the degree of dependency among observations in a geographic space. Classic spatial autocorrelation statistics include Moran's

Moran's I
In statistics, Moran's I is a measure of spatial autocorrelation developed by Patrick A.P. Moran. Spatial autocorrelation is characterized by a correlation in a signal among nearby locations in space. Spatial autocorrelation is more complex than one-dimensional autocorrelation because spatial...
and Geary's

Geary's C
Geary's C is a measure of spatial autocorrelation. Like autocorrelation, spatial autocorrelation means that adjacent observations of the same phenomenon are correlated. However, autocorrelation is about proximity in time. Spatial autocorrelation is about proximity in space...
. These require measuring a spatial weights matrix that reflects the intensity of the geographic relationship between observations in a neighborhood, e.g., the distances between neighbors, the lengths of shared border, or whether they fall into a specified directional class such as "west". Classic spatial autocorrelation statistics compare the spatial weights to the covariance relationship at pairs of locations. Spatial autocorrelation that is more positive than expected from random indicate the clustering of similar values across geographic space, while significant negative spatial autocorrelation indicates that neighboring values are more dissimilar than expected by chance, suggesting a spatial pattern similar to a chess board.
Spatial autocorrelation statistics such as Moran's
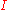 and Geary's
and Geary's  are global in the sense that they estimate the overall degree of spatial autocorrelation for a dataset. The possibility of spatial heterogeneity suggests that the estimated degree of autocorrelation may vary significantly across geographic space. Local spatial autocorrelation statistics provide estimates disaggregated to the level of the spatial analysis units, allowing assessment of the dependency relationships across space.
are global in the sense that they estimate the overall degree of spatial autocorrelation for a dataset. The possibility of spatial heterogeneity suggests that the estimated degree of autocorrelation may vary significantly across geographic space. Local spatial autocorrelation statistics provide estimates disaggregated to the level of the spatial analysis units, allowing assessment of the dependency relationships across space.  statistics compare neighborhoods to a global average and identify local regions of strong autocorrelation. Local versions of the
statistics compare neighborhoods to a global average and identify local regions of strong autocorrelation. Local versions of the 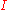 and
and  statistics are also available.
statistics are also available.Spatial interpolation
Spatial interpolation methods estimate the variables at unobserved locations in geographic space based on the values at observed locations. Basic methods include inverse distance weightingInverse distance weighting
Inverse distance weighting is a method for multivariate interpolation, a process of assigning values to unknown points by using values from usually scattered set of known points...
: this attenuates the variable with decreasing proximity from the observed location. Kriging
Kriging
Kriging is a group of geostatistical techniques to interpolate the value of a random field at an unobserved location from observations of its value at nearby locations....
is a more sophisticated method that interpolates across space according to a spatial lag relationship that has both systematic and random components. This can accommodate a wide range of spatial relationships for the hidden values between observed locations. Kriging provides optimal estimates given the hypothesized lag relationship, and error estimates can be mapped to determine if spatial patterns exist.
Spatial regression
Spatial regression methods capture spatial dependency in regression analysisRegression analysis
In statistics, regression analysis includes many techniques for modeling and analyzing several variables, when the focus is on the relationship between a dependent variable and one or more independent variables...
, avoiding statistical problems such as unstable parameters and unreliable significance tests, as well as providing information on spatial relationships among the variables involved. Depending on the specific technique, spatial dependency can enter the regression model as relationships between the independent variables and the dependent, between the dependent variables and a spatial lag of itself, or in the error terms. Geographically weighted regression (GWR) is a local version of spatial regression that generates parameters disaggregated by the spatial units of analysis. This allows assessment of the spatial heterogeneity in the estimated relationships between the independent and dependent variables. The use of Markov Chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
(MCMC) methods can allow the estimation of complex functions, such as Poisson-Gamma-CAR, Poisson-lognormal-SAR, or Overdispersed logit models.
Spatial interaction
Spatial interaction or "gravity modelGravity model
Gravity models are used in various social sciences to predict and describe certain behaviors that mimic gravitational interaction as described in Isaac Newton's law of gravity...
s" estimate the flow of people, material or information between locations in geographic space. Factors can include origin propulsive variables such as the number of commuters in residential areas, destination attractiveness variables such as the amount of office space in employment areas, and proximity relationships between the locations measured in terms such as driving distance or travel time. In addition, the topological, or connective
Geospatial topology
Geospatial topology studies the rules concerning the relationships between the points, lines, and polygons that represent the features of a geographic region. For example, where two polygons represent adjacent counties, typical topological rules would require that the counties share a common...
, relationships between areas must be identified, particularly considering the often conflicting relationship between distance and topology; for example, two spatially close neighborhoods may not display any significant interaction if they are separated by a highway. After specifying the functional forms of these relationships, the analyst can estimate model parameters using observed flow data and standard estimation techniques such as ordinary least squares or maximum likelihood. Competing destinations versions of spatial interaction models include the proximity among the destinations (or origins) in addition to the origin-destination proximity; this captures the effects of destination (origin) clustering on flows. Computational methods such as artificial neural networks can also estimate spatial interaction relationships among locations and can handle noisy and qualitative data.
Simulation and modeling
Spatial interaction models are aggregate and top-down: they specify an overall governing relationship for flow between locations. This characteristic is also shared by urban models such as those based on mathematical programming, flows among economic sectors, or bid-rent theory. An alternative modeling perspective is to represent the system at the highest possible level of disaggregation and study the bottom-up emergence of complex patterns and relationships from behavior and interactions at the individual level.Complex adaptive systems theory as applied to spatial analysis suggests that simple interactions among proximal entities can lead to intricate, persistent and functional spatial entities at aggregate levels. Two fundamentally spatial simulation methods are cellular automata and agent-based modeling. Cellular automata modeling imposes a fixed spatial framework such as grid cells and specifies rules that dictate the state of a cell based on the states of its neighboring cells. As time progresses, spatial patterns emerge as cells change states based on their neighbors; this alters the conditions for future time periods. For example, cells can represent locations in an urban area and their states can be different types of land use. Patterns that can emerge from the simple interactions of local land uses include office districts and urban sprawl. Agent-based modeling uses software entities (agents) that have purposeful behavior (goals) and can react, interact and modify their environment while seeking their objectives. Unlike the cells in cellular automata, agents can be mobile with respect to space. For example, one could model traffic flow and dynamics using agents representing individual vehicles that try to minimize travel time between specified origins and destinations. While pursuing minimal travel times, the agents must avoid collisions with other vehicles also seeking to minimize their travel times. Cellular automata and agent-based modeling are complementary modeling strategies. They can be integrated into a common geographic automata system where some agents are fixed while others are mobile.
Multiple-Point Geostatistics (MPS)
Spatial analysis of a conceptual geological model is the main purpose of any MPS algorithm. The method analyzes the spatial statistics of the geological model, called the training image, and generates realizations of the phenomena that honor those input multiple-point statistics.One of the recent technique to accomplish this task is the pattern-based method of Honarkhah. In this method, a distance-based approach is employed to analyze the patterns in the training image. This allows the reproduction of the multiple-point statistics, and the complex geometrical features of the given image. The final generated realizations of this, so called random field, can be used to quantify spatial uncertainty.
Geographic information science and spatial analysis
Geographic information systems (GIS) and the underlying geographic information scienceGeographic Information Science
Geographic information science is the academic theory behind the development, use, and application of geographic information systems...
that advances these technologies have a strong influence on spatial analysis. The increasing ability to capture and handle geographic data means that spatial analysis is occurring within increasingly data-rich environments. Geographic data capture systems include remotely sensed imagery, environmental monitoring systems such as intelligent transportation systems, and location-aware technologies such as mobile devices that can report location in near-real time. GIS provide platforms for managing these data, computing spatial relationships such as distance, connectivity and directional relationships between spatial units, and visualizing both the raw data and spatial analytic results within a cartographic context.

Geovisualization
Geovisualization, short for Geographic Visualization, refers to a set of tools and techniques supporting geospatial data analysis through the use of interactive visualization....
(GVis) combines scientific visualization with digital cartography to support the exploration and analysis of geographic data and information, including the results of spatial analysis or simulation. GVis leverages the human orientation towards visual information processing in the exploration, analysis and communication of geographic data and information. In contrast with traditional cartography, GVis is typically three or four-dimensional (the latter including time) and user-interactive.
Geographic knowledge discovery (GKD) is the human-centered process of applying efficient computational tools for exploring massive spatial database
Spatial Database
A spatial database is a database that is optimized to store and query data that is related to objects in space, including points, lines and polygons. While typical databases can understand various numeric and character types of data, additional functionality needs to be added for databases to...
s. GKD includes geographic data mining
Data mining
Data mining , a relatively young and interdisciplinary field of computer science is the process of discovering new patterns from large data sets involving methods at the intersection of artificial intelligence, machine learning, statistics and database systems...
, but also encompasses related activities such as data selection, data cleaning and pre-processing, and interpretation of results. GVis can also serve a central role in the GKD process. GKD is based on the premise that massive databases contain interesting (valid, novel, useful and understandable) patterns that standard analytical techniques cannot find. GKD can serve as a hypothesis-generating process for spatial analysis, producing tentative patterns and relationships that should be confirmed using spatial analytical techniques.
Spatial Decision Support System
Spatial Decision Support System
Spatial decision support systems developed in parallel with the concept of decision support systems .An sDSS is an interactive, computer-based system designed to support a user or group of users in achieving a higher effectiveness of decision making while solving a semi-structured spatial problem...
s (sDSS) take existing spatial data and use a variety of mathematical models to make projections into the future. This allows urban and regional planners to test intervention decisions prior to implementation.
See also
General topics- Mathematical StatisticsMathematical statisticsMathematical statistics is the study of statistics from a mathematical standpoint, using probability theory as well as other branches of mathematics such as linear algebra and analysis...
- Geographic information scienceGeographic Information ScienceGeographic information science is the academic theory behind the development, use, and application of geographic information systems...
- Spatial autocorrelation
- Complete spatial randomnessComplete spatial randomnessComplete spatial randomness describes a point process whereby point events occur within a given study area in a completely random fashion. Such a process is often modeled using only one parameter, i.e. the density of points, \rho within the defined area...
- Modifiable Areal Unit ProblemModifiable Areal Unit ProblemThe modifiable areal unit problem is a source of statistical bias that can radically affect the results of statistical hypothesis tests. It affects results when point-based measures of spatial phenomena are aggregated into districts. The resulting summary values are influenced by the choice of...
- Geospatial predictive modelingGeospatial predictive modelingGeospatial predictive modeling is conceptually rooted in the principle that the occurrences ofevents being modeled are limited in distribution...
- GeoComputationGeoComputationGeoComputation is an emergent paradigm for multidisciplinary/interdisciplinary research that enables the exploration of previously insoluble, extraordinarily intricate problems in geographic context.-Introduction:...
Specific applications
- Geographic information systems
- Geodemographic segmentationGeodemographic SegmentationIn marketing, Geodemographic segmentation is a multivariate statistical classification technique for discovering whether the individuals of a population fall into different groups by making quantitative comparisons of multiple characteristics with the assumption that the differences within any...
- Visibility analysis
- Fuzzy architectural spatial analysisFuzzy architectural spatial analysisFuzzy architectural spatial analysis is a spatial analysis method of analyzing the spatial formation and architectural space intensity within any architectural organization.Fuzzy architectural spatial analysis is used in architecture, interior design, urban planning and...
- Suitability analysisSuitability analysisSuitability Analysis is the process and procedures used to establish the suitability of a system - that is, the ability of a system to meet the needs of a or other .- Suitability in GIS context :...
- Extrapolation domain analysisExtrapolation domain analysisExtrapolation domain analysis is a methodology for identifying geographical areas that seem suitable for adoption of innovative ecosystem management practices on the basis of sites exhibiting similarity in conditions such as climatic, land use and socio-economic indicators...
- GeoinformaticsGeoinformaticsGeoinformatics is the science and the technology which develops and uses information science infrastructure to address the problems of geography, geosciences and related branches of engineering.-Overview:...
- Boundary problem (in spatial analysis)Boundary problem (in spatial analysis)A boundary problem in spatial analysis refers to a phenomenon in which geographical patterns are differentiated by the shape and arrangement of boundaries that are drawn for administrative or measurement purposes...
- Spatial epidemiologySpatial epidemiologySpatial epidemiology is a subfield of health geography focused on the study of the spatial distribution of disease.-See also:General topics* Cluster * Complete spatial randomness* Geographic information system* Geographic information science...
- Spatial econometricsSpatial econometricsSpatial Econometrics is the field where spatial analysis and econometrics intersect. In general, econometrics differs from other branches of statistics in focusing on theoretical models, whose parameters are estimated using regression analysis...
Further reading
- Abler, R., J. Adams, and P. Gould (1971) Spatial Organization–The Geographer's View of the World, Englewood Cliffs, NJ: Prentice-Hall.
- Anselin, L. (1995) "Local indicators of spatial association – LISA". Geographical Analysis, 27, 93–115.
- Banerjee, S., B.P. Carlin and A.E. Gelfand (2004). Hierarchical Modeling and Analysis for Spatial Data. Taylor and Francis: Chapman and Hall/CRC Press.
- Benenson, I. and P. M. Torrens. (2004). Geosimulation: Automata-Based Modeling of Urban Phenomena. Wiley.
- Fotheringham, A. S., C. Brunsdon and M. Charlton (2000) Quantitative Geography: Perspectives on Spatial Data Analysis, Sage.
- Fotheringham, A. S. and M. E. O'Kelly (1989) Spatial Interaction Models: Formulations and Applications, Kluwer Academic
- Fotheringham, A. S. and P. A. Rogerson (1993) "GIS and spatial analytical problems". International Journal of Geographical Information Systems, 7, 3–19.
- Goodchild, M. F. (1987) "A spatial analytical perspective on geographical information systems". International Journal of Geographical Information Systems, 1, 327–44.
- MacEachren, A. M.Alan MacEachrenAlan M. MacEachren is an American geographer, Professor of Geography and Director, GeoVISTA Center, Department of Geography, The Pennsylvania State University. He is known for his cross-disciplinary work in the fields of human-centered geographic visualization, scientific and information...
and D. R. F. Taylor (eds.) (1994) Visualization in Modern Cartography, Pergamon. - Levine, N. (2010). CrimeStat: A Spatial Statistics Program for the Analysis of Crime Incident Locations. Version 3.3. Ned Levine & Associates, Houston, TX and the National Institute of Justice, Washington, DC. Ch. 1-17 + 2 update chapters http://www.icpsr.umich.edu/CrimeStat
- Miller, H. J. (2004) "Tobler's First Law and spatial analysis". Annals of the Association of American Geographers, 94, 284–289.
- Miller, H. J. and J. Han (eds.) (2001) Geographic Data Mining and Knowledge Discovery, Taylor and Francis.
- O'Sullivan, D. and D. Unwin (2002) Geographic Information Analysis, Wiley.
- Parker, D. C., S. M. Manson, M.A. Janssen, M. J. Hoffmann and P. Deadman (2003) "Multi-agent systems for the simulation of land-use and land-cover change: A review". Annals of the Association of American Geographers, 93, 314–337.
- White, R. and G. Engelen (1997) "Cellular automata as the basis of integrated dynamic regional modelling". Environment and Planning B: Planning and Design, 24, 235–246.
- Fisher MM, Leung Y (2001) Geocomputational Modelling: techniques and applications. Springer Verlag, Berlin
- Fotheringham S, Clarke G, Abrahart B (1997) Geocomputation and GIS. Transactions in GIS 2:199-200
- Openshaw S and Abrahart RJ (2000) GeoComputation. CRC Press
- Diappi L (2004) Evolving Cities: Geocomputation in Territorial Planning. Ashgate, England
- Longley PA, Brooks SM, McDonnell R, Macmillan B (1998), Geocomputation, a primer. John Wiley and Sons, Chichester
- Ehlen J, Caldwell DR and Harding S (2002) GeoComputation: what is it?,Comput Environ and Urban Syst 26:257-265
- Gahegan M (1999) What is Geocomputation? Transaction in GIS 3:203-206
- Murgante B., Borruso G., Lapucci A. (2009) "Geocomputation and Urban Planning" Studies in Computational Intelligence, Vol. 176. Springer-Verlag, Berlin.
- Fischer M., Leung Y.(2010) "GeoComputational Modelling: Techniques and Applications" Advances in Spatial Science. Springer-Verlag, Berlin.
- Murgante B., Borruso G., Lapucci A. (2011) "Geocomputation, Sustainability and Environmental Planning" Studies in Computational Intelligence, Vol. 348. Springer-Verlag, Berlin.
External links
- ICA Commission on Geospatial Analysis and Modeling
- An educational resource about spatial statistics and geostatistics
- A comprehensive guide to principles, techniques & software tools
- Social and Spatial Inequalities
- National Center for Geographic Information and Analysis (NCGIA)
- International Cartographic Association (ICA), the world body for mapping and GIScience professionals

