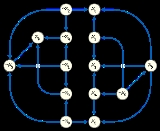
Skew-symmetric graph
Encyclopedia
In graph theory
, a branch of mathematics, a skew-symmetric graph is a directed graph
that is isomorphic
to its own transpose graph
, the graph formed by reversing all of its edges. The isomorphism is required to be an involution without any fixed points
.
Skew-symmetric graphs were first introduced under the name of antisymmetrical digraphs by . They arise in modeling the search for alternating paths and alternating cycles in algorithms for finding matchings in graphs, in testing whether a still life pattern in Conway's Game of Life
may be partitioned into simpler components, in graph drawing
, and in the implication graph
s used to efficiently solve the 2-satisfiability
problem.
One may use the third property to extend σ to an orientation-reversing function on the edges of G.
The transpose graph
of G is the graph formed by reversing every edge of G, and σ defines a graph isomorphism
from G to its transpose. However, in a skew-symmetric graph, it is additionally required that the isomorphism pair each vertex with a different vertex, rather than allowing a vertex to be mapped to itself by the isomorphism or to group more than two vertices in a cycle of isomorphisms.
A path or cycle in a skew-symmetric graph is said to be regular if, for each vertex v of the path or cycle, the corresponding vertex σ(v) is not part of the path or cycle.
come together: if a train enters a switch via a track that comes in from one direction, it must exit via a track in the other direction. The problem of finding non-self-intersecting smooth curves between given points in a train track comes up in testing whether certain kinds of graph drawing
s are valid and may be modeled as the search for a regular path in a skew-symmetric graph.
A closely related concept is the bidirected graph
of , a graph in which each of the two ends of each edge may be either a head or a tail, independently of the other end. A bidirected graph may be interpreted as a switch graph by letting the partition of edges at each vertex be determined by the partition of endpoints at that vertex into heads and tails; however, swapping the roles of heads and tails at a single vertex produces a different bidirected graph but the same switch graph. For the correspondence between bidirected graphs and skew-symmetric graphs see .
To form a skew-symmetric graph from a switch graph G, create for each vertex v of G two vertices v0 and v1, and let σ(vi) = v1 − i. For each edge e = (u,v) of G, create two directed edges in the skew-symmetric graph, one oriented from u to v and one oriented from v to u. If e is in the first subset of edges at v, connect these two edges out of v0 and into v1, while if e is in the second subset, connect these two edges out of v1 and into v0.
In the other direction, given a skew-symmetric graph G, one may form a switch graph that has one vertex for every corresponding pair of vertices in G and one undirected edge for every corresponding pair of edges in G. The undirected edges at each vertex of the switch graph may be partitioned into two subsets according to which vertex of the switch graph they go out of and come in to.
A regular path or cycle of a skew-symmetric graph corresponds to a path or cycle in the switch graph that uses at most one edge from each subset of edges at each of its vertices.
As showed, an alternating path or cycle in an undirected graph may be modeled as a regular path or cycle in a skew-symmetric directed graph. To create a skew-symmetric graph from an undirected graph G with a specified matching M, view G as a switch graph in which the edges at each vertex are partitioned into matched and unmatched edges; an alternating path in G is then a regular path in this switch graph and an alternating cycle in G is a regular cycle in the switch graph.
generalized alternating path algorithms to show that the existence of a regular path between any two vertices of a skew-symmetric graph may be tested in linear time. Given additionally a non-negative length function on the edges of the graph that assigns the same length to any edge e and to σ(e), the shortest regular path connecting a given pair of nodes in a skew-symmetric graph with m edges and n vertices may be tested in time O(m log n). If the length function is allowed to have negative lengths, the existence of a negative regular cycle may be tested in polynomial time.
Along with the path problems arising in matchings, skew-symmetric generalizations of the max-flow min-cut theorem
have also been studied .
may be partitioned into two smaller still lifes if and only if an associated switch graph contains a regular cycle. As he shows, for switch graphs with at most three edges per vertex, this may be tested in polynomial time by repeatedly removing bridges
(edges the removal of which disconnects the graph) and vertices at which all edges belong to a single partition until no more such simplifications may be performed. If the result is an empty graph, there is no regular cycle; otherwise, a regular cycle may be found in any remaining bridgeless component. The repeated search for bridges in this algorithm may be performed efficiently using a dynamic graph algorithm of .
Similar bridge-removal techniques in the context of matching were previously considered by .
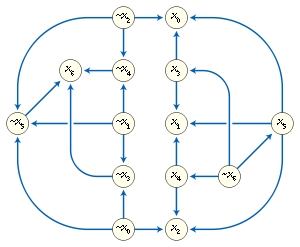An instance of the 2-satisfiability
problem, that is, a Boolean expression in conjunctive normal form
with two variables or negations of variables per clause, may be transformed into an implication graph
by replacing each clause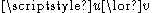
by the two implications
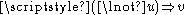and 
. This graph has a vertex for each variable or negated variable, and a directed edge for each implication; it is, by construction, skew-symmetric, with a correspondence σ that maps each variable to its negation.
As showed, a satisfying assignment to the 2-satisfiability instance is equivalent to a partition of this implication graph into two subsets of vertices, S and σ(S), such that no edge starts in S and ends in σ(S). If such a partition exists, a satisfying assignment may be formed by assigning a true value to every variable in S and a false value to every variable in σ(S). This may be done if and only if no strongly connected component
of the graph contains both some vertex v and its complementary vertex σ(v). If two vertices belong to the same strongly connected component, the corresponding variables or negated variables are constrained to equal each other in any satisfying assignment of the 2-satisfiability instance. The total time for testing strong connectivity and finding a partition of the implication graph is linear in the size of the given 2-CNF expression.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, a branch of mathematics, a skew-symmetric graph is a directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
that is isomorphic
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
to its own transpose graph
Transpose graph
In the mathematical and algorithmic study of graph theory, the converse, transpose or reverse of a directed graph G is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in G...
, the graph formed by reversing all of its edges. The isomorphism is required to be an involution without any fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
.
Skew-symmetric graphs were first introduced under the name of antisymmetrical digraphs by . They arise in modeling the search for alternating paths and alternating cycles in algorithms for finding matchings in graphs, in testing whether a still life pattern in Conway's Game of Life
Conway's Game of Life
The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970....
may be partitioned into simpler components, in graph drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
, and in the implication graph
Implication graph
In mathematical logic, an implication graph is a skew-symmetric directed graph G composed of vertex set V and directed edge set E. Each vertex in V represents the truth status of a Boolean literal, and each directed edge from vertex u to vertex v represents the material implication "If the literal...
s used to efficiently solve the 2-satisfiability
2-satisfiability
In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
problem.
Definition
As defined, e.g., by , a skew-symmetric graph G is a directed graph, together with a function σ mapping vertices of G to other vertices of G, satisfying the following properties:- For every vertex v, σ(v) ≠ v
- For every vertex v, σ(σ(v)) = v
- For every edge (u,v), (σ(v),σ(u)) must also be an edge.
One may use the third property to extend σ to an orientation-reversing function on the edges of G.
The transpose graph
Transpose graph
In the mathematical and algorithmic study of graph theory, the converse, transpose or reverse of a directed graph G is another directed graph on the same set of vertices with all of the edges reversed compared to the orientation of the corresponding edges in G...
of G is the graph formed by reversing every edge of G, and σ defines a graph isomorphism
Graph isomorphism
In graph theory, an isomorphism of graphs G and H is a bijection between the vertex sets of G and H f \colon V \to V \,\!such that any two vertices u and v of G are adjacent in G if and only if ƒ and ƒ are adjacent in H...
from G to its transpose. However, in a skew-symmetric graph, it is additionally required that the isomorphism pair each vertex with a different vertex, rather than allowing a vertex to be mapped to itself by the isomorphism or to group more than two vertices in a cycle of isomorphisms.
A path or cycle in a skew-symmetric graph is said to be regular if, for each vertex v of the path or cycle, the corresponding vertex σ(v) is not part of the path or cycle.
Switch graphs and bidirected graphs
A skew-symmetric graph may equivalently be defined in terms of a switch graph (to use the terminology of ), an undirected graph in which the edges incident to each vertex are partitioned into two subsets. Each vertex of the switch graph corresponds to two vertices of the skew-symmetric graph, and each edge of the switch graph corresponds to two edges of the skew-symmetric graph. This equivalence is the one used by to model problems of matching in terms of skew-symmetric graphs; in that application, the two subsets of edges at each vertex are the unmatched edges and the matched edges. Cook visualizes the vertices of a switch graph as points where multiple tracks of a train trackTrain track
In the mathematical area of topology, a train track is a family of curves embedded on a surface, meeting the following conditions:#The curves meet at a finite set of vertices called switches....
come together: if a train enters a switch via a track that comes in from one direction, it must exit via a track in the other direction. The problem of finding non-self-intersecting smooth curves between given points in a train track comes up in testing whether certain kinds of graph drawing
Graph drawing
Graph drawing is an area of mathematics and computer science combining methods from geometric graph theory and information visualization to derive two-dimensional depictions of graphs arising from applications such as social network analysis, cartography, and bioinformatics...
s are valid and may be modeled as the search for a regular path in a skew-symmetric graph.
A closely related concept is the bidirected graph
Bidirected graph
In the mathematical domain of graph theory, a bidirected graph is a graph in which each edge is given an independent orientation at each end...
of , a graph in which each of the two ends of each edge may be either a head or a tail, independently of the other end. A bidirected graph may be interpreted as a switch graph by letting the partition of edges at each vertex be determined by the partition of endpoints at that vertex into heads and tails; however, swapping the roles of heads and tails at a single vertex produces a different bidirected graph but the same switch graph. For the correspondence between bidirected graphs and skew-symmetric graphs see .
To form a skew-symmetric graph from a switch graph G, create for each vertex v of G two vertices v0 and v1, and let σ(vi) = v1 − i. For each edge e = (u,v) of G, create two directed edges in the skew-symmetric graph, one oriented from u to v and one oriented from v to u. If e is in the first subset of edges at v, connect these two edges out of v0 and into v1, while if e is in the second subset, connect these two edges out of v1 and into v0.
In the other direction, given a skew-symmetric graph G, one may form a switch graph that has one vertex for every corresponding pair of vertices in G and one undirected edge for every corresponding pair of edges in G. The undirected edges at each vertex of the switch graph may be partitioned into two subsets according to which vertex of the switch graph they go out of and come in to.
A regular path or cycle of a skew-symmetric graph corresponds to a path or cycle in the switch graph that uses at most one edge from each subset of edges at each of its vertices.
Matching
In constructing matchings in undirected graphs, it is important to find alternating paths, paths of vertices that start and end at unmatched vertices, in which the edges at odd positions in the path are not part of a given partial matching and in which the edges at even positions in the path are part of the matching. By removing the matched edges of such a path from a matching, and adding the unmatched edges, one can increase the size of the matching. Similarly, cycles that alternate between matched and unmatched edges are of importance in weighted matching problems.As showed, an alternating path or cycle in an undirected graph may be modeled as a regular path or cycle in a skew-symmetric directed graph. To create a skew-symmetric graph from an undirected graph G with a specified matching M, view G as a switch graph in which the edges at each vertex are partitioned into matched and unmatched edges; an alternating path in G is then a regular path in this switch graph and an alternating cycle in G is a regular cycle in the switch graph.
generalized alternating path algorithms to show that the existence of a regular path between any two vertices of a skew-symmetric graph may be tested in linear time. Given additionally a non-negative length function on the edges of the graph that assigns the same length to any edge e and to σ(e), the shortest regular path connecting a given pair of nodes in a skew-symmetric graph with m edges and n vertices may be tested in time O(m log n). If the length function is allowed to have negative lengths, the existence of a negative regular cycle may be tested in polynomial time.
Along with the path problems arising in matchings, skew-symmetric generalizations of the max-flow min-cut theorem
Max-flow min-cut theorem
In optimization theory, the max-flow min-cut theorem states that in a flow network, the maximum amount of flow passing from the source to the sink is equal to the minimum capacity which when removed in a specific way from the network causes the situation that no flow can pass from the source to the...
have also been studied .
Still life theory
shows that a still life pattern in Conway's Game of LifeConway's Game of Life
The Game of Life, also known simply as Life, is a cellular automaton devised by the British mathematician John Horton Conway in 1970....
may be partitioned into two smaller still lifes if and only if an associated switch graph contains a regular cycle. As he shows, for switch graphs with at most three edges per vertex, this may be tested in polynomial time by repeatedly removing bridges
Bridge (graph theory)
In graph theory, a bridge is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle....
(edges the removal of which disconnects the graph) and vertices at which all edges belong to a single partition until no more such simplifications may be performed. If the result is an empty graph, there is no regular cycle; otherwise, a regular cycle may be found in any remaining bridgeless component. The repeated search for bridges in this algorithm may be performed efficiently using a dynamic graph algorithm of .
Similar bridge-removal techniques in the context of matching were previously considered by .
Satisfiability
2-satisfiability
In computer science, 2-satisfiability is the problem of determining whether a collection of two-valued variables with constraints on pairs of variables can be assigned values satisfying all the constraints...
problem, that is, a Boolean expression in conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
with two variables or negations of variables per clause, may be transformed into an implication graph
Implication graph
In mathematical logic, an implication graph is a skew-symmetric directed graph G composed of vertex set V and directed edge set E. Each vertex in V represents the truth status of a Boolean literal, and each directed edge from vertex u to vertex v represents the material implication "If the literal...
by replacing each clause
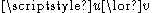by the two implications 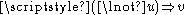and . This graph has a vertex for each variable or negated variable, and a directed edge for each implication; it is, by construction, skew-symmetric, with a correspondence σ that maps each variable to its negation.As showed, a satisfying assignment to the 2-satisfiability instance is equivalent to a partition of this implication graph into two subsets of vertices, S and σ(S), such that no edge starts in S and ends in σ(S). If such a partition exists, a satisfying assignment may be formed by assigning a true value to every variable in S and a false value to every variable in σ(S). This may be done if and only if no strongly connected component
Strongly connected component
A directed graph is called strongly connected if there is a path from each vertex in the graph to every other vertex. In particular, this means paths in each direction; a path from a to b and also a path from b to a....
of the graph contains both some vertex v and its complementary vertex σ(v). If two vertices belong to the same strongly connected component, the corresponding variables or negated variables are constrained to equal each other in any satisfying assignment of the 2-satisfiability instance. The total time for testing strong connectivity and finding a partition of the implication graph is linear in the size of the given 2-CNF expression.