Shock capturing methods
Encyclopedia
In computational fluid dynamics
, shock-capturing methods are a class of techniques for computing inviscid flow
s with shock wave
s. Computation of flow through shock waves is an extremely difficult task because such flows result in sharp, discontinuous changes in flow variables pressure, temperature, density, and velocity across the shock.
The shock capturing methods are relatively simple compared to the more elaborate shock fitting methods. However, the shock waves predicted by shock-capturing methods are generally not sharp and smear over several grid points. Also, classical shock-capturing methods have the disadvantages that unphysical oscillations (Gibbs phenomenon
) may develop in the vicinity of strong shocks.
can be written as
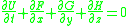
where the vectors U, F, G, and H are given by
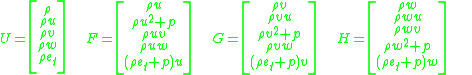
where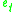
is the total energy (internal energy + kinetic energy + potential energy) per unit mass. That is
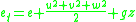
The Euler equation may be integrated with any of the shock-capturing methods available to obtain the solution.
in contrast to classical symmetric or central discretization. Upwind-type differencing schemes attempt to discretize hyperbolic partial differential equations by using differencing biased in the direction determined by the sign of the characteristic speeds. On the other hand, symmetric or central schemes do not consider any information about the wave propagation in the discretization.
No matter what type of shock-capturing scheme is used, a stable calculation in presence of shock waves requires a certain amount of numerical dissipation, in order to avoid the formation of unphysical numerical oscillations. In the case of classical shock-capturing methods, numerical dissipation terms are usually linear and the same amount is uniformly applied at all grid points. Classical shock-capturing methods only exhibit accurate results in the case of
smooth and weak-shock solution, but when strong shock waves are present in the solution, non-linear instabilities and oscillations can arise across discontinuities. Modern shock-capturing methods have, however, a non-linear numerical dissipation, with an automatic feedback mechanism which adjusts the amount of dissipation in any cell of the mesh, in accord to the gradients in the solution. These schemes have proven to be stable and accurate even for problems
containing strong shock waves.
Some of the well known classical shock-capturing methods include the MacCormack method
(uses a discretization scheme for the numerical solution of hyperbolic partial differential equations), Lax–Wendroff method
(based on finite differences, uses a numerical method for the solution of hyperbolic partial differential equation
s), and Beam-Warming method. Examples of modern shock-capturing schemes include, higher order Total Variation Diminishing
(TVD) schemes first proposed by Harten
, Flux-Corrected Transport scheme
introduced by Boris and Book, Monotonic Upstream-centered Schemes for Conservation Laws
(MUSCL) based on Godunov approach
and introduced by van Leer
, various Essentially Non-Oscillatory schemes (ENO) proposed by Harten et al., and Piecewise Parabolic Method (PPM) proposed by Woodward and Colella
. Another important class of high resolution schemes belongs to the approximate Riemann solver
s proposed by Roe and by Osher
. The schemes proposed by Jameson
and Baker, where linear numerical dissipation terms depend on
non-linear switch functions, fall in between the classical and modern shock-capturing methods.
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
, shock-capturing methods are a class of techniques for computing inviscid flow
Inviscid flow
In fluid dynamics there are problems that are easily solved by using the simplifying assumption of an ideal fluid that has no viscosity. The flow of a fluid that is assumed to have no viscosity is called inviscid flow....
s with shock wave
Shock wave
A shock wave is a type of propagating disturbance. Like an ordinary wave, it carries energy and can propagate through a medium or in some cases in the absence of a material medium, through a field such as the electromagnetic field...
s. Computation of flow through shock waves is an extremely difficult task because such flows result in sharp, discontinuous changes in flow variables pressure, temperature, density, and velocity across the shock.
Explanation
In shock-capturing approach the governing equations of inviscid flows (Euler equations) are cast in conservation form and any shock waves or discontinuities are computed as part of the solution. Here, no special treatment is employed to take care of the shocks themselves. This is in contrast to the shock-fitting method, where shock waves are explicitly introduced in the solution using appropriate shock relations (Rankine-Hugoniot relations).The shock capturing methods are relatively simple compared to the more elaborate shock fitting methods. However, the shock waves predicted by shock-capturing methods are generally not sharp and smear over several grid points. Also, classical shock-capturing methods have the disadvantages that unphysical oscillations (Gibbs phenomenon
Gibbs phenomenon
In mathematics, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity: the nth partial sum of the Fourier series has large...
) may develop in the vicinity of strong shocks.
Euler equation
The Euler equations are the governing equations for inviscid flows. To implement shock-capturing methods, the conservation form of the Euler equations are used. For a flow without external heat transfer and work transfer (isoenergetic flow), the conservation form of the Euler equation in Cartesian coordinate systemCartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
can be written as
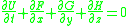
where the vectors U, F, G, and H are given by
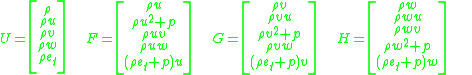
where
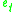is the total energy (internal energy + kinetic energy + potential energy) per unit mass. That is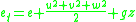The Euler equation may be integrated with any of the shock-capturing methods available to obtain the solution.
Classical and modern shock capturing methods
From an historical point of view, shock-capturing methods can be classified into two general categories: viz., classical methods and modern shock capturing methods (also called high-resolution schemes). Modern shock-capturing methods are generally upwind basedUpwind scheme
In computational fluid dynamics, upwind schemes denote a class of numerical discretization methods for solving hyperbolic partial differential equations. Upwind schemes use an adaptive or solution-sensitive finite difference stencil to numerically simulate more properly the direction of propagation...
in contrast to classical symmetric or central discretization. Upwind-type differencing schemes attempt to discretize hyperbolic partial differential equations by using differencing biased in the direction determined by the sign of the characteristic speeds. On the other hand, symmetric or central schemes do not consider any information about the wave propagation in the discretization.
No matter what type of shock-capturing scheme is used, a stable calculation in presence of shock waves requires a certain amount of numerical dissipation, in order to avoid the formation of unphysical numerical oscillations. In the case of classical shock-capturing methods, numerical dissipation terms are usually linear and the same amount is uniformly applied at all grid points. Classical shock-capturing methods only exhibit accurate results in the case of
smooth and weak-shock solution, but when strong shock waves are present in the solution, non-linear instabilities and oscillations can arise across discontinuities. Modern shock-capturing methods have, however, a non-linear numerical dissipation, with an automatic feedback mechanism which adjusts the amount of dissipation in any cell of the mesh, in accord to the gradients in the solution. These schemes have proven to be stable and accurate even for problems
containing strong shock waves.
Some of the well known classical shock-capturing methods include the MacCormack method
MacCormack method
In computational fluid dynamics, the MacCormack method is a widely used discretization scheme for the numerical solution of hyperbolic partial differential equations. This second-order finite difference method is introduced by Robert W. MacCormack in 1969...
(uses a discretization scheme for the numerical solution of hyperbolic partial differential equations), Lax–Wendroff method
Lax–Wendroff method
The Lax–Wendroff method, named after Peter Lax and Burton Wendroff, is a numerical method for the solution of hyperbolic partial differential equations, based on finite differences...
(based on finite differences, uses a numerical method for the solution of hyperbolic partial differential equation
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s), and Beam-Warming method. Examples of modern shock-capturing schemes include, higher order Total Variation Diminishing
Total variation diminishing
In numerical methods, total variation diminishing is a property of certain discretization schemes used to solve hyperbolic partial differential equations...
(TVD) schemes first proposed by Harten
Ami Harten
Amiram Harten was an American/Israeli applied mathematician. Harten made fundamental contribution to the development of high-resolution schemes for the solution of hyperbolic partial differential equations...
, Flux-Corrected Transport scheme
Flux-Corrected Transport
Flux-Corrected Transport is a conservative shock-capturing scheme for solving Euler equations and other hyperbolic equations which occur in gasdynamics, aerodynamics, and magnetohydrodynamics. It is especially useful for solving problems involving shock or contact discontinuities. An FCT algorithm...
introduced by Boris and Book, Monotonic Upstream-centered Schemes for Conservation Laws
MUSCL scheme
In the study of partial differential equations, the MUSCL scheme is a finite volume method that can provide highly accurate numerical solutions for a given system, even in cases where the solutions exhibit shocks, discontinuities, or large gradients...
(MUSCL) based on Godunov approach
Godunov's scheme
In numerical analysis and computational fluid dynamics, Godunov's scheme is a conservative numerical scheme, suggested by S. K. Godunov in 1959, for solving partial differential equations...
and introduced by van Leer
Bram van Leer
Bram van Leer is the Arthur B. Modine Professor of aerospace engineering at the University of Michigan, in Ann Arbor. He specialises in Computational fluid dynamics , fluid dynamics, and numerical analysis where he has made substantial contributions.-Research work:Professor van Leer developed...
, various Essentially Non-Oscillatory schemes (ENO) proposed by Harten et al., and Piecewise Parabolic Method (PPM) proposed by Woodward and Colella
Phillip Colella
Phillip Colella is an American applied mathematician and the Head of the Applied Numerical Algorithms Group at the National Energy Research Scientific Computing Center, Lawrence Berkeley National Laboratory. He has also worked at Lawrence Livermore National Laboratory...
. Another important class of high resolution schemes belongs to the approximate Riemann solver
Riemann solver
A Riemann solver is a numerical method used to solve a Riemann problem. They are heavily used in computational fluid dynamics and computational magnetohydrodynamics.-Exact solvers:...
s proposed by Roe and by Osher
Stanley Osher
Stanley Osher is an American mathematician, known for his many contributions in shock capturing, level set methods, and PDE-based methods in computer vision and image processing...
. The schemes proposed by Jameson
Antony Jameson
Antony Jameson is the Thomas V. Jones Professor of Engineering in the Department of Aeronautics & Astronautics at Stanford University. Jameson is known for his pioneering work in the field of Computational Fluid Dynamics...
and Baker, where linear numerical dissipation terms depend on
non-linear switch functions, fall in between the classical and modern shock-capturing methods.
Books
- Anderson, J. D.John D. AndersonJohn D. Anderson, Jr. is the Curator of Aerodynamics at the National Air and Space Museum at the Smithsonian Institution in Washington, DC and Professor Emeritus in the Department of Aerospace Engineering at the University of Maryland, College Park. Anderson is active and known for his...
, "Modern Compressible Flow with Historical Perspective", McGraw-Hill (2004). - Hirsch, C., "Numerical Computation of Internal and External Flows", Vol. II, 2nd ed., Butterworth-Heinemann (2007).
- Laney, C. B., "Computational Gasdynamics", Cambridge Univ. Press 1998).
- LeVeque, R. J.Randall J. LeVequeRandall J. LeVeque is a Professor of Applied Mathematics at University of Washington who works in many fields including numerical analysis computational fluid dynamics, and mathematical theory of conservation laws. Among other contributions, he has devised a numerical technique called immersed...
, "Numerical Methods for Conservation Laws", Birkhauser-Verlag (1992). - Tannehill, J. C., Anderson, D. A.Dale A. AndersonDale A. Anderson is an American aerospace engineer and computational fluid dynamicist. Anderson was the Professor of Aerospace Engineering and Vice President for Research and Dean of Graduate Students at the University of Texas at Arlington, United States...
, and Pletcher, R. H., "Computational Fluid Dynamics and Heat Transfer", 2nd ed., Taylor & Francis (1997). - Toro, E. F., "Riemann Solvers and Numerical Methods for Fluid Dynamics", 2nd ed., Springer-Verlag (1999).
Technical Papers
- Boris, J. P. and Book, D. L., "Flux-Corrected Transport III. Minimal Error FCT Algorithms", J. Comput. Phys., 20, 397-431 (1976).
- Colella, P.Phillip ColellaPhillip Colella is an American applied mathematician and the Head of the Applied Numerical Algorithms Group at the National Energy Research Scientific Computing Center, Lawrence Berkeley National Laboratory. He has also worked at Lawrence Livermore National Laboratory...
and Woodward, P., "The Piecewise parabolic Method (PPM) for Gasdynamical Simulations", J. Comput. Phys., 54, 174-201 (1984).
- Godunov, S. K.Sergei K. GodunovSergei Konstantinovich Godunov is professor at the Sobolev Institute of Mathematics of the Russian Academy of Sciences in Novosibirsk, Russia....
, "A Difference Scheme for Numerical Computation of Discontinuous Solution of Hyperbolic Equations", Math. Sbornik, 47, 271-306 (1959).
- Harten, A.Ami HartenAmiram Harten was an American/Israeli applied mathematician. Harten made fundamental contribution to the development of high-resolution schemes for the solution of hyperbolic partial differential equations...
, "High Resolution Schemes for Hyperbolic Conservation Laws", J. Comput. Phys., 49, 357-293 (1983).
- Harten, A., Engquist, B.Björn EngquistBjörn Engquist has been a leading contributor in the areas of multiscale modeling and scientific computing, and a productive educator of applied mathematicians.He received his Ph.D...
, Osher, S.Stanley OsherStanley Osher is an American mathematician, known for his many contributions in shock capturing, level set methods, and PDE-based methods in computer vision and image processing...
, and Chakravarthy, S. R., "Uniformly High Order Accurate Essentially Non-Oscillatory Schemes III", J. Comput. Phys., 71, 231-303 (1987).
- Jameson, A.Antony JamesonAntony Jameson is the Thomas V. Jones Professor of Engineering in the Department of Aeronautics & Astronautics at Stanford University. Jameson is known for his pioneering work in the field of Computational Fluid Dynamics...
and Baker, T., "Solution of the Euler Equations for Complex Configurations", AIAA Paper, 83-1929 (1983).
- MacCormack, R. W., "The Effect of Viscosity in Hypervelocity Impact Cratering", AIAA Paper, 69-354 (1969).
- Roe, P. L.Philip L. RoePhilip L. Roe is a Professor of Aerospace Engineering at the University of Michigan in Ann Arbor. He is known for his work in the field of Computational Fluid Dynamics and Magnetohydrodynamics. Roe made fundamental contributions to the development of high-resolution schemes for hyperbolic...
, "Approximate Riemann Solvers, Parameter Vectors and Difference Schemes", J. Comput. Phys. 43, 357-372 (1981).
- Shu, C.-W.Chi-Wang ShuChi-Wang Shu is the Theodore B. Stowell University Professor of Applied Mathematics at the Brown University. He is known for his research work in the fields of computational fluid dynamics, Numerical solutions of conservation laws and Hamilton–Jacobi type equations...
, Osher, S., "Efficient Implementation of Essentially Non-Oscillatory Shock Capturing Schemes", J. Comput. Phys., 77, 439-471 (1988).
- van Leer, B.Bram van LeerBram van Leer is the Arthur B. Modine Professor of aerospace engineering at the University of Michigan, in Ann Arbor. He specialises in Computational fluid dynamics , fluid dynamics, and numerical analysis where he has made substantial contributions.-Research work:Professor van Leer developed...
, "Towards the Ultimate Conservative Difference Scheme V; A Second-order Sequel to Godunov's Sequel", J. Comput. Phys., 32, 101-136, (1979).