
Upwind scheme
Encyclopedia
In computational fluid dynamics
, upwind schemes denote a class of numerical discretization
methods for solving hyperbolic partial differential equation
s. Upwind schemes use an adaptive or solution-sensitive finite difference
stencil to numerically simulate more properly the direction of propagation of information in a flow field. The upwind schemes attempt to discretize hyperbolic partial differential equations by using differencing biased in the direction determined by the sign of the characteristic speeds. Historically, the origin of upwind methods can be traced back to the work of Courant
, Isaacson, and Rees who proposed the CIR method.
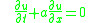
It describes a wave propagating in the -direction with a velocity
-direction with a velocity  . The preceding equation
. The preceding equation
is also a mathematical model for one-dimensional linear advection. Consider a typical grid point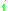 in the
in the
domain. In a one-dimensional domain, there are only two directions associated with point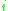 - left and
- left and
right. If is positive the left side is called upwind side and right side is the downwind side. Similarly, if
is positive the left side is called upwind side and right side is the downwind side. Similarly, if  is negative the left side is called downwind side and right side is the upwind side. If the finite difference scheme for the spatial derivative,
is negative the left side is called downwind side and right side is the upwind side. If the finite difference scheme for the spatial derivative, 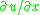 contains more
contains more
points in the upwind side, the scheme is called an upwind-biased or simply an upwind scheme.
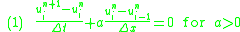
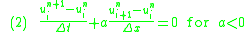
Defining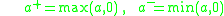
and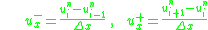
the two conditional equations (1) and (2) can be combined and written in a compact form as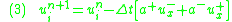
Equation (3) is a general way of writing any upwind-type schemes.
The upwind scheme is stable
if the following Courant–Friedrichs–Lewy condition
(CFL) condition is satisfied.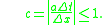
A Taylor series
analysis of the upwind scheme discussed above will show that it is first-order accurate in space and time. The first-order upwind scheme introduces severe numerical diffusion
in the solution where large gradients exist.
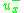 in equation (3) is defined as
in equation (3) is defined as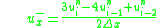
and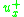 is defined as
is defined as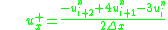
This scheme is less diffusive compared to the first-order accurate scheme and is called linear upwind differencing (LUD) scheme.
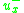 in equation (3) is defined as
in equation (3) is defined as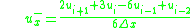
and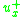 is defined as
is defined as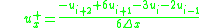
This scheme is less diffusive compared to the second-order accurate scheme. However, it is known to introduce slight dispersive errors in the region where the gradient is high.
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
, upwind schemes denote a class of numerical discretization
Discretization
In mathematics, discretization concerns the process of transferring continuous models and equations into discrete counterparts. This process is usually carried out as a first step toward making them suitable for numerical evaluation and implementation on digital computers...
methods for solving hyperbolic partial differential equation
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s. Upwind schemes use an adaptive or solution-sensitive finite difference
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
stencil to numerically simulate more properly the direction of propagation of information in a flow field. The upwind schemes attempt to discretize hyperbolic partial differential equations by using differencing biased in the direction determined by the sign of the characteristic speeds. Historically, the origin of upwind methods can be traced back to the work of Courant
Richard Courant
Richard Courant was a German American mathematician.- Life :Courant was born in Lublinitz in the German Empire's Prussian Province of Silesia. During his youth, his parents had to move quite often, to Glatz, Breslau, and in 1905 to Berlin. He stayed in Breslau and entered the university there...
, Isaacson, and Rees who proposed the CIR method.
Model equation
To illustrate the method, consider the following one-dimensional linear wave equation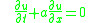
It describes a wave propagating in the
 -direction with a velocity
-direction with a velocity  . The preceding equation
. The preceding equationis also a mathematical model for one-dimensional linear advection. Consider a typical grid point
 in the
in thedomain. In a one-dimensional domain, there are only two directions associated with point
 - left and
- left andright. If
 is positive the left side is called upwind side and right side is the downwind side. Similarly, if
is positive the left side is called upwind side and right side is the downwind side. Similarly, if  is negative the left side is called downwind side and right side is the upwind side. If the finite difference scheme for the spatial derivative,
is negative the left side is called downwind side and right side is the upwind side. If the finite difference scheme for the spatial derivative, 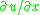 contains more
contains morepoints in the upwind side, the scheme is called an upwind-biased or simply an upwind scheme.
First-order upwind scheme
The simplest upwind scheme possible is the first-order upwind scheme. It is given by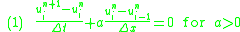
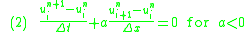
Defining
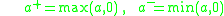
and
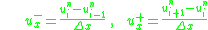
the two conditional equations (1) and (2) can be combined and written in a compact form as
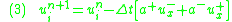
Equation (3) is a general way of writing any upwind-type schemes.
The upwind scheme is stable
Numerical stability
In the mathematical subfield of numerical analysis, numerical stability is a desirable property of numerical algorithms. The precise definition of stability depends on the context, but it is related to the accuracy of the algorithm....
if the following Courant–Friedrichs–Lewy condition
Courant–Friedrichs–Lewy condition
In mathematics, the Courant–Friedrichs–Lewy condition is a necessary condition for convergence while solving certain partial differential equations numerically by the method of finite differences. It arises when explicit time-marching schemes are used for the numerical solution...
(CFL) condition is satisfied.
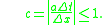
A Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
analysis of the upwind scheme discussed above will show that it is first-order accurate in space and time. The first-order upwind scheme introduces severe numerical diffusion
Numerical diffusion
Numerical diffusion is a difficulty with computer simulations of continua wherein the simulated medium exhibits a higher diffusivity than the true medium...
in the solution where large gradients exist.
Second-order upwind scheme
The spatial accuracy of the first-order upwind scheme can be improved by choosing a more accurate finite difference stencil for the approximation of spatial derivative. For the second-order upwind scheme,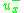 in equation (3) is defined as
in equation (3) is defined as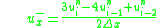
and
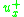 is defined as
is defined as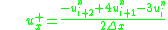
This scheme is less diffusive compared to the first-order accurate scheme and is called linear upwind differencing (LUD) scheme.
Third-order upwind scheme
For the third-order upwind scheme,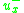 in equation (3) is defined as
in equation (3) is defined as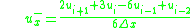
and
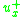 is defined as
is defined as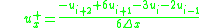
This scheme is less diffusive compared to the second-order accurate scheme. However, it is known to introduce slight dispersive errors in the region where the gradient is high.

