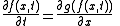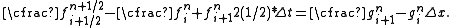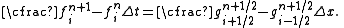The Lax–Wendroff method, named after Peter Lax

Peter Lax

Peter David Lax is a mathematician working in the areas of pure and applied mathematics. He has made important contributions to integrable systems, fluid dynamics and shock waves, solitonic physics, hyperbolic conservation laws, and mathematical and scientific computing, among other fields...

 and Burton Wendroff

Burton Wendroff

Burton Wendroff is an American applied mathematician and an Adjunct Professor at the Department of Mathematics and Statistics, University of New Mexico. He is also a retired Fellow and Associate at the Los Alamos National Laboratory...

, is a numerical

Numerical analysis

Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....

 method for the solution of hyperbolic partial differential equation

Hyperbolic partial differential equation

In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...

s, based on finite difference

Finite difference

A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...

s. It is second-order accurate in both space and time.

Suppose one has an equation of the following form:

where x and t are independent variables, and the initial state, ƒ(x, 0) is given.

The first step in the Lax–Wendroff method calculates values for ƒ(x, t) at half time steps, t_n + 1/2 and half grid points, x_i + 1/2. In the second step values at t_n + 1 are calculated using the data for t_n and t_n + 1/2.

First (Lax) step:

Second step:

This method can be further applied to some systems of partial differential equations.