MacCormack method
Encyclopedia
In computational fluid dynamics
, the MacCormack method is a widely used discretization scheme for the numerical solution of hyperbolic partial differential equation
s. This second-order finite difference method
is introduced by Robert W. MacCormack in 1969. The MacCormack method is very elegant and easy to understand and program.
but is much simpler in application. To illustrate the algorithm, consider the following first order hyperbolic equation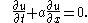
The application of MacCormack method to the above equation proceeds in two steps; a predictor step which is followed by a corrector step.
Predictor step: In the predictor step, a "provisional" value of
at time level 
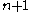(denoted by 
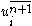) is estimated as follows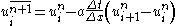
It may be noted that the above equation is obtained by replacing the spatial and temporal derivatives in the wave equation using forward differences.
Corrector step: In the corrector step, the predicted value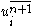
is corrected according to the equation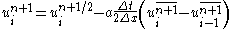
Note that the corrector step uses backward finite difference approximations for spatial derivative. Note also that the time-step used in the corrector step is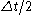
in contrast to the 
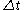used in the predictor step.
Replacing the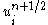
term by the temporal average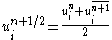
to obtain the corrector step as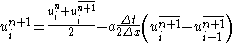
, etc.) The order of differencing can be reversed for the time step (i.e., forward/backward followed by backward/forward). For nonlinear equations, this procedure provides the best results. For linear equations, the MacCormack scheme is equivalent to the Lax–Wendroff scheme.
Unlike first-order upwind scheme
, the MacCormack does not introduce diffusive errors
in the solution. However, it is known to introduce dispersive errors (Gibbs phenomenon
) in the region where the gradient is high.
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
, the MacCormack method is a widely used discretization scheme for the numerical solution of hyperbolic partial differential equation
Hyperbolic partial differential equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s. This second-order finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
is introduced by Robert W. MacCormack in 1969. The MacCormack method is very elegant and easy to understand and program.
The algorithm
The MacCormack method is a variation of the two-step Lax–Wendroff schemeLax–Wendroff method
The Lax–Wendroff method, named after Peter Lax and Burton Wendroff, is a numerical method for the solution of hyperbolic partial differential equations, based on finite differences...
but is much simpler in application. To illustrate the algorithm, consider the following first order hyperbolic equation
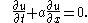
The application of MacCormack method to the above equation proceeds in two steps; a predictor step which is followed by a corrector step.
Predictor step: In the predictor step, a "provisional" value of
at time level 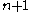(denoted by 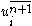) is estimated as follows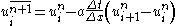It may be noted that the above equation is obtained by replacing the spatial and temporal derivatives in the wave equation using forward differences.
Corrector step: In the corrector step, the predicted value
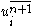is corrected according to the equation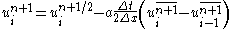Note that the corrector step uses backward finite difference approximations for spatial derivative. Note also that the time-step used in the corrector step is
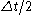in contrast to the 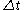used in the predictor step.Replacing the
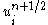term by the temporal average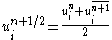to obtain the corrector step as
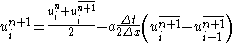
Some remarks
The MacCormack method is well suited for nonlinear equations (Inviscid Burgers equation, Euler equationsEuler equations
In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,...
, etc.) The order of differencing can be reversed for the time step (i.e., forward/backward followed by backward/forward). For nonlinear equations, this procedure provides the best results. For linear equations, the MacCormack scheme is equivalent to the Lax–Wendroff scheme.
Unlike first-order upwind scheme
Upwind scheme
In computational fluid dynamics, upwind schemes denote a class of numerical discretization methods for solving hyperbolic partial differential equations. Upwind schemes use an adaptive or solution-sensitive finite difference stencil to numerically simulate more properly the direction of propagation...
, the MacCormack does not introduce diffusive errors
Numerical diffusion
Numerical diffusion is a difficulty with computer simulations of continua wherein the simulated medium exhibits a higher diffusivity than the true medium...
in the solution. However, it is known to introduce dispersive errors (Gibbs phenomenon
Gibbs phenomenon
In mathematics, the Gibbs phenomenon, named after the American physicist J. Willard Gibbs, is the peculiar manner in which the Fourier series of a piecewise continuously differentiable periodic function behaves at a jump discontinuity: the nth partial sum of the Fourier series has large...
) in the region where the gradient is high.
See also
- Lax–Wendroff methodLax–Wendroff methodThe Lax–Wendroff method, named after Peter Lax and Burton Wendroff, is a numerical method for the solution of hyperbolic partial differential equations, based on finite differences...
- Upwind schemeUpwind schemeIn computational fluid dynamics, upwind schemes denote a class of numerical discretization methods for solving hyperbolic partial differential equations. Upwind schemes use an adaptive or solution-sensitive finite difference stencil to numerically simulate more properly the direction of propagation...
- Hyperbolic partial differential equationHyperbolic partial differential equationIn mathematics, a hyperbolic partial differential equation of order n is a partial differential equation that, roughly speaking, has a well-posed initial value problem for the first n−1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along...
s