
Shell integration
Encyclopedia
Shell integration is a means of calculating
the volume
of a solid of revolution
, when integrating along an axis perpendicular to the axis of revolution.
It makes use of the so-called "representative cylinder
". Intuitively speaking, part of the graph of a function
is rotated around an axis, and is modelled by an infinite number of hollow pipes, all infinitely thin.
The idea is that a "representative rectangle
" (used in the most basic forms of integration
– such as ∫ x dx) can be rotated about the axis of revolution
; thus generating a hollow cylinder. Integration, as an accumulative process, can then calculate the integrated volume of a "family" of shells (a shell being the outer edge of a hollow cylinder) – as volume is the antiderivative
of area, if one can calculate the lateral surface
area of a shell, one can then calculate its volume.
The necessary equation
, for calculating such a volume, V, is slightly different depending on which axis is serving as the axis of revolution. These equations note that the lateral surface area of a shell equals: 2 pi
(π) multiplied
by the cylinder's average radius
, p(x), multiplied by the height
of the cylinder, h(x). One can calculate the volume of a representative shell by: 2π * p(x) * h(x) * dx, where dx is the thickness of the shell – that being some number approaching zero
.
Shell integration can be considered a special case of evaluating a double integral in polar coordinates.
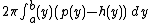
if the rotation is around the x-axis (horizontal axis of revolution), or
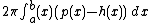
if the rotation is around the y-axis (vertical axis of revolution).
So here the function p(x) is the distance from the axis and h(x) is the length of the shell, generally the function being rotated. The values for a and b are the limits of integration, the starting and stopping points of the rotated shape (note the limits are units of the Axis of Revolution).
The surface area of Cylinder by double Integration, derived from following equation:
S=∫_0^l▒∫_0^r▒〖2π r dr dθ〗
And we know that, the Length of arc is:
z=ab=rθ→dz=r dθ
In conclusion, the surface area is:
Calculation
A calculation is a deliberate process for transforming one or more inputs into one or more results, with variable change.The term is used in a variety of senses, from the very definite arithmetical calculation of using an algorithm to the vague heuristics of calculating a strategy in a competition...
the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a solid of revolution
Solid of revolution
In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....
, when integrating along an axis perpendicular to the axis of revolution.
It makes use of the so-called "representative cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
". Intuitively speaking, part of the graph of a function
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
is rotated around an axis, and is modelled by an infinite number of hollow pipes, all infinitely thin.
The idea is that a "representative rectangle
Rectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
" (used in the most basic forms of integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
– such as ∫ x dx) can be rotated about the axis of revolution
Solid of revolution
In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....
; thus generating a hollow cylinder. Integration, as an accumulative process, can then calculate the integrated volume of a "family" of shells (a shell being the outer edge of a hollow cylinder) – as volume is the antiderivative
Antiderivative
In calculus, an "anti-derivative", antiderivative, primitive integral or indefinite integralof a function f is a function F whose derivative is equal to f, i.e., F ′ = f...
of area, if one can calculate the lateral surface
Lateral surface
In geometry, the lateral surface of a solid is the face or surface of the solid on its sides. That is, any face or surface that is not a base.-Sources:*...
area of a shell, one can then calculate its volume.
The necessary equation
Equation
An equation is a mathematical statement that asserts the equality of two expressions. In modern notation, this is written by placing the expressions on either side of an equals sign , for examplex + 3 = 5\,asserts that x+3 is equal to 5...
, for calculating such a volume, V, is slightly different depending on which axis is serving as the axis of revolution. These equations note that the lateral surface area of a shell equals: 2 pi
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
(π) multiplied
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
by the cylinder's average radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
, p(x), multiplied by the height
Height
Height is the measurement of vertical distance, but has two meanings in common use. It can either indicate how "tall" something is, or how "high up" it is. For example "The height of the building is 50 m" or "The height of the airplane is 10,000 m"...
of the cylinder, h(x). One can calculate the volume of a representative shell by: 2π * p(x) * h(x) * dx, where dx is the thickness of the shell – that being some number approaching zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
.
Shell integration can be considered a special case of evaluating a double integral in polar coordinates.
Calculation
Mathematically, this method is represented by: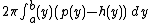
if the rotation is around the x-axis (horizontal axis of revolution), or
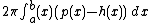
if the rotation is around the y-axis (vertical axis of revolution).
So here the function p(x) is the distance from the axis and h(x) is the length of the shell, generally the function being rotated. The values for a and b are the limits of integration, the starting and stopping points of the rotated shape (note the limits are units of the Axis of Revolution).
See also
- Solid of revolutionSolid of revolutionIn mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....
- Disk integrationDisk integrationDisk integration, , is a means of calculating the volume of a solid of revolution of a solid-state material, when integrating along the axis of revolution. This method models the generated 3 dimensional shape as a "stack" of an infinite number of disks of infinitesimal thickness...
- RadiusRadiusIn classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
The surface area of Cylinder by double Integration, derived from following equation:
S=∫_0^l▒∫_0^r▒〖2π r dr dθ〗
And we know that, the Length of arc is:
z=ab=rθ→dz=r dθ
In conclusion, the surface area is:

