Disk integration
Encyclopedia
Disk integration, is a means of calculating
the volume
of a solid of revolution
of a solid-state material, when integrating along the axis of revolution. This method models the generated 3 dimensional shape as a "stack" of an infinite number of disks (of varying radius) of infinitesimal thickness. It is possible to use "washers" instead of "disks" (the washer method) to obtain "hollow" solids of revolutions, and uses the same principles that underlie disk integration.
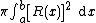
where R(x) is the distance between the function and the axis of rotation. This works only if the axis of rotation is horizontal (example: y = 3 or some other constant).
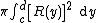
where R(y) is the distance between the function and the axis of rotation. This works only if the axis of rotation is vertical (example: x = 4 or some other constant).
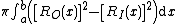
where RO(x) is the function that is farthest from the axis of rotation and RI(x) is the function that is closest to the axis of rotation. One should take caution not to evaluate the square of the difference of the two functions, but to evaluate the difference of the squares of the two functions.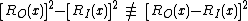
NOTE: the above formula only works for revolutions about the x-axis.
To rotate about any horizontal axis, simply subtract from that axis each formula:
if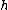
is the value of a horizontal axis, then the volume =
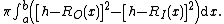
For example, to rotate the region between
and 
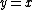
along the axis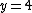
, you would have to integrate as follows:
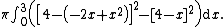
The bounds of integration are the zeros of the first equation minus the second. Note that when you integrate along an axis other than the
, the further axis may not be that obvious. In the previous example, even though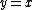 
is further up than 
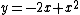, it is the inner axis since it is closer to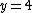 
The same idea can be applied to both the y-axis and any other vertical axis. You simply must solve each equation for
before you plug them into the integration formula.
Calculation
A calculation is a deliberate process for transforming one or more inputs into one or more results, with variable change.The term is used in a variety of senses, from the very definite arithmetical calculation of using an algorithm to the vague heuristics of calculating a strategy in a competition...
the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
of a solid of revolution
Solid of revolution
In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....
of a solid-state material, when integrating along the axis of revolution. This method models the generated 3 dimensional shape as a "stack" of an infinite number of disks (of varying radius) of infinitesimal thickness. It is possible to use "washers" instead of "disks" (the washer method) to obtain "hollow" solids of revolutions, and uses the same principles that underlie disk integration.
Function of x
If the function to be revolved is a function of x, the following integral represents the volume of the solid of revolution: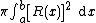where R(x) is the distance between the function and the axis of rotation. This works only if the axis of rotation is horizontal (example: y = 3 or some other constant).
Function of y
If the function to be revolved is a function of y, the following integral will obtain the volume of the solid of revolution: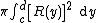where R(y) is the distance between the function and the axis of rotation. This works only if the axis of rotation is vertical (example: x = 4 or some other constant).
Washer method
To obtain a "hollow" solid of revolution (often called the "Washer method"), the procedure would be to take the volume of the inner solid of revolution and subtract it from the volume of the outer solid of revolution. This can be calculated in a single integral similar to the following: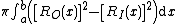where RO(x) is the function that is farthest from the axis of rotation and RI(x) is the function that is closest to the axis of rotation. One should take caution not to evaluate the square of the difference of the two functions, but to evaluate the difference of the squares of the two functions.
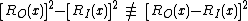
NOTE: the above formula only works for revolutions about the x-axis.
To rotate about any horizontal axis, simply subtract from that axis each formula:
if
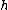is the value of a horizontal axis, then the volume =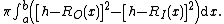For example, to rotate the region between
and 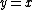along the axis
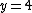, you would have to integrate as follows: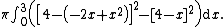The bounds of integration are the zeros of the first equation minus the second. Note that when you integrate along an axis other than the
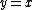, the further axis may not be that obvious. In the previous example, even though is further up than 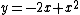, it is the inner axis since it is closer to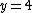 The same idea can be applied to both the y-axis and any other vertical axis. You simply must solve each equation for
before you plug them into the integration formula.