
Shape factor (image analysis and microscopy)
Encyclopedia
Shape factors are dimensionless quantities
used in image analysis
and microscopy
that numerically describe the shape of a particle, independent of its size. Shape factors are calculated from measured dimension
s, such as diameter
, chord
lengths, area
, perimeter
, centroid
, moments
, etc. The dimensions of the particles are usually measured
from two-dimensional cross-sections
or projections
, as in a microscope field, but shape factors also apply to three-dimensional objects. The particles could be the grains in a metallurgical
or ceramic microstructure
, or the microorganisms in a culture
, for example. The dimensionless quantities often represent the degree of deviation
from an ideal shape, such as a circle
, sphere or equilateral polyhedron
. Shape factors are often normalized, that is, the value ranges from zero to one. A shape factor equal to one usually represents an ideal case or maximum symmetry, such as a circle, sphere, square or cube.

The normalized aspect ratio varies from approaching zero for a very elongated particle, such as a grain in a cold-worked metal, to near unity for an equiaxed grain. The reciprocal of the right side of the above equation is also used, such that the AR varies from one to approaching infinity.
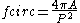
The circularity of a circle is 1, and much less than one for a starfish footprint. The reciprocal of the circularity equation is also used, such that fcirc varies from one for a circle to infinity.
in of the particle around its principal axes.

shape factor is a function of the polar second moment in of a particle and a circle of equal area A.
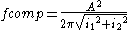
The fcomp of a circle is one, and much less than one for the cross-section of an I-beam
.
shape factor of the perimeter is a function of the convex portion Pcvx of the perimeter to the total.

Some properties of metals and ceramics, such as fracture toughness
, have been linked to grain shapes.
, the largest island in the world, has an area of 2,166,086 km2; a coastline (perimeter) of 39,330 km; a north-south length of 2670 km; and an east-west length of 1290 km. The aspect ratio of Greenland is

The circularity of Greenland is
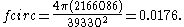
The aspect ratio is agreeable with an eyeball-estimate on a globe. Such an estimate on a flat map would be less accurate due to the distortion of high-latitude
projections
. The circularity is deceptively low, due to the fjord
s that give Greenland a very jagged coastline
. A low value of circularity does not necessarily indicate a lack of symmetry! And shape factors are not limited to microscopic objects!
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
used in image analysis
Image analysis
Image analysis is the extraction of meaningful information from images; mainly from digital images by means of digital image processing techniques...
and microscopy
Microscope
A microscope is an instrument used to see objects that are too small for the naked eye. The science of investigating small objects using such an instrument is called microscopy...
that numerically describe the shape of a particle, independent of its size. Shape factors are calculated from measured dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
s, such as diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
, chord
Chord (geometry)
A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...
lengths, area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
, perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
, centroid
Centroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
, moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
, etc. The dimensions of the particles are usually measured
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
from two-dimensional cross-sections
Cross section (geometry)
In geometry, a cross-section is the intersection of a figure in 2-dimensional space with a line, or of a body in 3-dimensional space with a plane, etc...
or projections
Orthographic projection
Orthographic projection is a means of representing a three-dimensional object in two dimensions. It is a form of parallel projection, where all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface...
, as in a microscope field, but shape factors also apply to three-dimensional objects. The particles could be the grains in a metallurgical
Metallography
Metallography is the study of the physical structure and components of metals, typically using microscopy.Ceramic and polymeric materials may also be prepared using metallographic techniques, hence the terms ceramography, plastography and, collectively, materialography.-Preparing metallographic...
or ceramic microstructure
Ceramography
Ceramography is the art and science of preparation, examination and evaluation of ceramic microstructures. Ceramography can be thought of as the metallography of ceramics. The microstructure is the structure level of approximately 0.1 to 100 µm, between the minimum wavelength of visible light and...
, or the microorganisms in a culture
Microbiological culture
A microbiological culture, or microbial culture, is a method of multiplying microbial organisms by letting them reproduce in predetermined culture media under controlled laboratory conditions. Microbial cultures are used to determine the type of organism, its abundance in the sample being tested,...
, for example. The dimensionless quantities often represent the degree of deviation
Deviation (statistics)
In mathematics and statistics, deviation is a measure of difference for interval and ratio variables between the observed value and the mean. The sign of deviation , reports the direction of that difference...
from an ideal shape, such as a circle
Roundness
*Roundness — sharpness of handwriting patterns*Roundness — measure of sharpness of a particle's corners*Roundness — roundness of clastic particles...
, sphere or equilateral polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
. Shape factors are often normalized, that is, the value ranges from zero to one. A shape factor equal to one usually represents an ideal case or maximum symmetry, such as a circle, sphere, square or cube.
Aspect ratio
- The most common shape factor is the aspect ratioAspect ratioThe aspect ratio of a shape is the ratio of its longer dimension to its shorter dimension. It may be applied to two characteristic dimensions of a three-dimensional shape, such as the ratio of the longest and shortest axis, or for symmetrical objects that are described by just two measurements,...
, a function of the largest diameter and the smallest diameter orthogonalOrthogonalityOrthogonality occurs when two things can vary independently, they are uncorrelated, or they are perpendicular.-Mathematics:In mathematics, two vectors are orthogonal if they are perpendicular, i.e., they form a right angle...
to it:

The normalized aspect ratio varies from approaching zero for a very elongated particle, such as a grain in a cold-worked metal, to near unity for an equiaxed grain. The reciprocal of the right side of the above equation is also used, such that the AR varies from one to approaching infinity.
Circularity
Another very common shape factor is the circularity, a function of the perimeter P and the area A: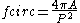
The circularity of a circle is 1, and much less than one for a starfish footprint. The reciprocal of the circularity equation is also used, such that fcirc varies from one for a circle to infinity.
Elongation shape factor
The less-common elongation shape factor is defined as the square root of the ratio of the two second momentsMoment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
in of the particle around its principal axes.

Compactness shape factor
The compactnessCompactness measure of a shape
The compactness measure of a shape, sometimes called the shape factor, is a numerical quantity representing the degree to which a shape is compact. The meaning of "compact" here is not related to the topological notion of compact space. Various compactness measures are used...
shape factor is a function of the polar second moment in of a particle and a circle of equal area A.
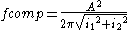
The fcomp of a circle is one, and much less than one for the cross-section of an I-beam
I-beam
-beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web...
.
Waviness shape factor
The wavinessWaviness
Waviness is the measure of the more widely spaced component of surface texture. It is a broader view of roughness because it is more strictly defined as "the irregularities whose spacing is greater than the roughness sampling length"...
shape factor of the perimeter is a function of the convex portion Pcvx of the perimeter to the total.

Some properties of metals and ceramics, such as fracture toughness
Fracture toughness
In materials science, fracture toughness is a property which describes the ability of a material containing a crack to resist fracture, and is one of the most important properties of any material for virtually all design applications. The fracture toughness of a material is determined from the...
, have been linked to grain shapes.
An application of shape factors
GreenlandGreenland
Greenland is an autonomous country within the Kingdom of Denmark, located between the Arctic and Atlantic Oceans, east of the Canadian Arctic Archipelago. Though physiographically a part of the continent of North America, Greenland has been politically and culturally associated with Europe for...
, the largest island in the world, has an area of 2,166,086 km2; a coastline (perimeter) of 39,330 km; a north-south length of 2670 km; and an east-west length of 1290 km. The aspect ratio of Greenland is

The circularity of Greenland is
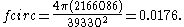
The aspect ratio is agreeable with an eyeball-estimate on a globe. Such an estimate on a flat map would be less accurate due to the distortion of high-latitude
Latitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
projections
Orthographic projection (cartography)
An orthographic projection is a map projection of cartography. Like the stereographic projection and gnomonic projection, orthographic projection is a perspective projection, in which the sphere is projected onto a tangent plane or secant plane. The point of perspective for the orthographic...
. The circularity is deceptively low, due to the fjord
Fjord
Geologically, a fjord is a long, narrow inlet with steep sides or cliffs, created in a valley carved by glacial activity.-Formation:A fjord is formed when a glacier cuts a U-shaped valley by abrasion of the surrounding bedrock. Glacial melting is accompanied by rebound of Earth's crust as the ice...
s that give Greenland a very jagged coastline
Coastline paradox
The coastline paradox is the counterintuitive observation that the coastline of a landmass does not have a well-defined length. This results from the fractal-like properties of coastlines. It was first observed by Lewis Fry Richardson....
. A low value of circularity does not necessarily indicate a lack of symmetry! And shape factors are not limited to microscopic objects!
Further reading
- J.C. Rust & R.T. Dehoff, Practical Stereology, 2nd Ed., Kluwer Academic, 2000.
- E.E. Underwood, Quantitative Stereology, Addison-Wesley Publishing Co., 1970.
- G.F. VanderVoort, Metallography: Principles and Practice, ASM International, 1984.

