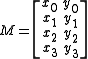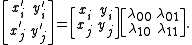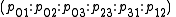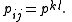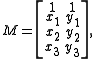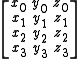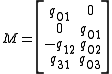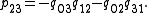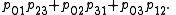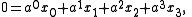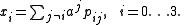
Plücker coordinates
Encyclopedia
In geometry
, Plücker coordinates, introduced by Julius Plücker
in the 19th century, are a way to assign six homogenous coordinates to each line
in projective 3-space
, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines in P3 and points on a quadric
in P5 (projective 5-space). A predecessor and special case of Grassmann coordinates (which describe k-dimensional linear subspaces, or flats, in an n-dimensional Euclidean space
), Plücker coordinates arise naturally in geometric algebra
. They have proved useful for computer graphics
, and also can be extended to coordinates for the screws and wrenches
in the theory of kinematics
used for robot control
.
 A line L in 3-dimensional Euclidean space
A line L in 3-dimensional Euclidean space
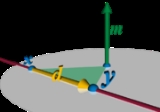
is determined by two distinct points that it contains, or by two distinct planes that contain it. Consider the first case, with points x = (x1,x2,x3) and y = (y1,y2,y3). The vector displacement from x to y is nonzero because the points are distinct, and represents the direction of the line. That is, every displacement between points on L is a scalar multiple of d = y−x. If a physical particle of unit mass were to move from x to y, it would have a moment
about the origin. The geometric equivalent is a vector whose direction is perpendicular to the plane containing L and the origin, and whose length equals twice the area of the triangle formed by the displacement and the origin. Treating the points as displacements from the origin, the moment is m = x×y, where "×" denotes the vector cross product
. The area of the triangle is proportional to the length of the segment between x and y, considered as the base of the triangle; it is not changed by sliding the base along the line, parallel to itself. By definition the moment vector is perpendicular to every displacement along the line, so d•m = 0, where "•" denotes the vector dot product
.
Although neither d nor m alone is sufficient to determine L, together the pair does so uniquely, up to a common (nonzero) scalar multiple which depends on the distance between x and y. That is, the coordinates
may be considered homogeneous coordinates
for L, in the sense that all pairs (λd:λm), for λ ≠ 0, can be produced by points on L and only L, and any such pair determines a unique line so long as d is not zero and d•m = 0. Furthermore, this approach extends to include points, lines
, and a plane
"at infinity", in the sense of projective geometry
.
Alternatively, let the equations for points x of two distinct planes containing L be
Then their respective planes are perpendicular to vectors a and b, and the direction of L must be perpendicular to both. Hence we may set d = a×b, which is nonzero because a and b are neither zero nor parallel (the planes being distinct and intersecting). If point x satisfies both plane equations, then it also satisfies the linear combination
That is, m = a b − b a is a vector perpendicular to displacements to points on L from the origin; it is, in fact, a moment consistent with the d previously defined from a and b.
Although the usual algebraic definition tends to obscure the relationship, (d:m) are the Plücker coordinates of L.
(x0:x1:x2:x3) and (y0:y1:y2:y3), respectively. Let M be the 4×2 matrix with these coordinates as columns.
Because x and y are distinct points, the columns of M are linearly independent
; M has rank
2. Let M′ be a second matrix, with columns x′ and y′ a different pair of distinct points on L. Then the columns of M′ are linear combination
s of the columns of M; so for some 2×2 nonsingular matrix Λ,
In particular, rows i and j of M′ and M are related by
Therefore, the determinant of the left side 2×2 matrix equals the product of the determinants of the right side 2×2 matrices, the latter of which is a fixed scalar, det Λ.
This implies pii = 0 and pij = −pji, reducing the possibilities to only six (4 choose
2) independent quantities. As we have seen, the sixtuple
is uniquely determined by L, up to a common nonzero scale factor. Furthermore, all six components cannot be zero, because if they were, all 2×2 subdeterminants in M would be zero and the rank of M at most one, contradicting the assumption that x and y are distinct. Thus the Plücker coordinates of L, as suggested by the colons, may be considered homogeneous coordinates of a point in a 5-dimensional projective space.
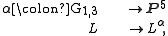
where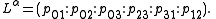
We define dual Plücker coordinate pij as the determinant of columns i and j of N,
Dual coordinates are convenient in some computations, and we can show that they are equivalent to primary coordinates. Specifically, let (i,j,k,l) be an even permutation of (0,1,2,3); then
and setting x = (x1,x2,x3) and y = (y1,y2,y3), we have d = (p01,p02,p03) and m = (p23,p31,p12).
Dually, we have d = (p23,p31,p12) and m = (p01,p02,p03).
are linearly dependent, so that the rank of this larger matrix is still 2. This implies that all 3×3 submatrices have determinant zero, generating four (4 choose 3) plane equations, such as
The four possible planes obtained are as follows.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Plücker coordinates, introduced by Julius Plücker
Julius Plücker
Julius Plücker was a German mathematician and physicist. He made fundamental contributions to the field of analytical geometry and was a pioneer in the investigations of cathode rays that led eventually to the discovery of the electron. He also vastly extended the study of Lamé curves.- Early...
in the 19th century, are a way to assign six homogenous coordinates to each line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
in projective 3-space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
, P3. Because they satisfy a quadratic constraint, they establish a one-to-one correspondence between the 4-dimensional space of lines in P3 and points on a quadric
Quadric (projective geometry)
In projective geometry a quadric is the set of points of a projective space where a certain quadratic form on the homogeneous coordinates becomes zero...
in P5 (projective 5-space). A predecessor and special case of Grassmann coordinates (which describe k-dimensional linear subspaces, or flats, in an n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
), Plücker coordinates arise naturally in geometric algebra
Geometric algebra
Geometric algebra , together with the associated Geometric calculus, provides a comprehensive alternative approach to the algebraic representation of classical, computational and relativistic geometry. GA now finds application in all of physics, in graphics and in robotics...
. They have proved useful for computer graphics
Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, and also can be extended to coordinates for the screws and wrenches
Screw theory
Screw theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies....
in the theory of kinematics
Kinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
used for robot control
Robot control
-See also:* Control theory* Mobile robot navigation* Robot kinematics* Simultaneous localization and mapping* Robot locomotion* Motion planning* Robot learning* Vision Based Robot Control...
.
Geometric intuition

Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is determined by two distinct points that it contains, or by two distinct planes that contain it. Consider the first case, with points x = (x1,x2,x3) and y = (y1,y2,y3). The vector displacement from x to y is nonzero because the points are distinct, and represents the direction of the line. That is, every displacement between points on L is a scalar multiple of d = y−x. If a physical particle of unit mass were to move from x to y, it would have a moment
Moment (physics)
In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...
about the origin. The geometric equivalent is a vector whose direction is perpendicular to the plane containing L and the origin, and whose length equals twice the area of the triangle formed by the displacement and the origin. Treating the points as displacements from the origin, the moment is m = x×y, where "×" denotes the vector cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
. The area of the triangle is proportional to the length of the segment between x and y, considered as the base of the triangle; it is not changed by sliding the base along the line, parallel to itself. By definition the moment vector is perpendicular to every displacement along the line, so d•m = 0, where "•" denotes the vector dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
.
Although neither d nor m alone is sufficient to determine L, together the pair does so uniquely, up to a common (nonzero) scalar multiple which depends on the distance between x and y. That is, the coordinates
- (d:m) = (d1:d2:d3:m1:m2:m3)
may be considered homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
for L, in the sense that all pairs (λd:λm), for λ ≠ 0, can be produced by points on L and only L, and any such pair determines a unique line so long as d is not zero and d•m = 0. Furthermore, this approach extends to include points, lines
Line at infinity
In geometry and topology, the line at infinity is a line that is added to the real plane in order to give closure to, and remove the exceptional cases from, the incidence properties of the resulting projective plane. The line at infinity is also called the ideal line.-Geometric formulation:In...
, and a plane
Plane at infinity
In projective geometry, the plane at infinity is a projective plane which is added to the affine 3-space in order to give it closure of incidence properties. The result of the addition is the projective 3-space, P^3...
"at infinity", in the sense of projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
.
- Example. Let x = (2,3,7) and y = (2,1,0). Then (d:m) = (0:−2:−7:−7:14:−4).
Alternatively, let the equations for points x of two distinct planes containing L be
- 0 = a + a•x
- 0 = b + b•x .
Then their respective planes are perpendicular to vectors a and b, and the direction of L must be perpendicular to both. Hence we may set d = a×b, which is nonzero because a and b are neither zero nor parallel (the planes being distinct and intersecting). If point x satisfies both plane equations, then it also satisfies the linear combination
| 0 | = a (b + b•x) − b (a + a•x) |
| = (a b − b a)•x . |
That is, m = a b − b a is a vector perpendicular to displacements to points on L from the origin; it is, in fact, a moment consistent with the d previously defined from a and b.
- Example. Let a0 = 2, a = (−1,0,0) and b0 = −7, b = (0,7,−2). Then (d:m) = (0:−2:−7:−7:14:−4).
Although the usual algebraic definition tends to obscure the relationship, (d:m) are the Plücker coordinates of L.
Algebraic definition
In a 3-dimensional projective space, P3, let L be a line containing distinct points x and y with homogeneous coordinatesHomogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
(x0:x1:x2:x3) and (y0:y1:y2:y3), respectively. Let M be the 4×2 matrix with these coordinates as columns.
Because x and y are distinct points, the columns of M are linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
; M has rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
2. Let M′ be a second matrix, with columns x′ and y′ a different pair of distinct points on L. Then the columns of M′ are linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
s of the columns of M; so for some 2×2 nonsingular matrix Λ,
In particular, rows i and j of M′ and M are related by
Therefore, the determinant of the left side 2×2 matrix equals the product of the determinants of the right side 2×2 matrices, the latter of which is a fixed scalar, det Λ.
Primary coordinates
With this motivation, we define Plücker coordinate pij as the determinant of rows i and j of M, 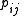 |
 |
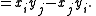 |
This implies pii = 0 and pij = −pji, reducing the possibilities to only six (4 choose
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
2) independent quantities. As we have seen, the sixtuple
is uniquely determined by L, up to a common nonzero scale factor. Furthermore, all six components cannot be zero, because if they were, all 2×2 subdeterminants in M would be zero and the rank of M at most one, contradicting the assumption that x and y are distinct. Thus the Plücker coordinates of L, as suggested by the colons, may be considered homogeneous coordinates of a point in a 5-dimensional projective space.
Plücker map
Denote the set of all lines (linear images of P1) in P3 by G1,3. We thus have a map: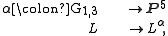
where
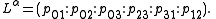
Dual coordinates
Alternatively, let L be a line contained in distinct planes a and b with homogeneous coefficients (a0:a1:a2:a3) and (b0:b1:b2:b3), respectively. (The first plane equation is 0 = ∑k akxk, for example.) Let N be the 2×4 matrix with these coordinates as rows.We define dual Plücker coordinate pij as the determinant of columns i and j of N,
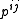 |
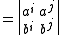 |
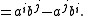 |
Dual coordinates are convenient in some computations, and we can show that they are equivalent to primary coordinates. Specifically, let (i,j,k,l) be an even permutation of (0,1,2,3); then
Geometry
To relate back to the geometric intuition, take x0 = 0 as the plane at infinity; thus the coordinates of points not at infinity can be normalized so that x0 = 1. Then M becomesand setting x = (x1,x2,x3) and y = (y1,y2,y3), we have d = (p01,p02,p03) and m = (p23,p31,p12).
Dually, we have d = (p23,p31,p12) and m = (p01,p02,p03).
Plane equations
If the point z = (z0:z1:z2:z3) lies on L, then the columns ofare linearly dependent, so that the rank of this larger matrix is still 2. This implies that all 3×3 submatrices have determinant zero, generating four (4 choose 3) plane equations, such as
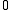 |
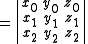 |
 |
|
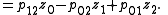 |
|
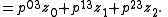 |
The four possible planes obtained are as follows.
-

Using dual coordinates, and letting (a0:a1:a2:a3) be the line coefficients, each of these is simply ai = pij, or
Each Plücker coordinate appears in two of the four equations, each time multiplying a different variable; and as at least one of the coordinates is nonzero, we are guaranteed non-vacuous equations for two distinct planes intersecting in L. Thus the Plücker coordinates of a line determine that line uniquely, and the map α is an injectionInjective functionIn mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
.
Quadratic relation
The image of α is not the complete set of points in P5; the Plücker coordinates of a line L satisfy the quadratic Plücker relation
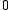
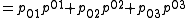
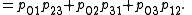
For proof, write this homogeneous polynomial as determinants and use Laplace expansionLaplace expansionIn linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
(in reverse).
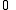
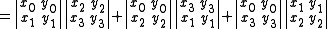
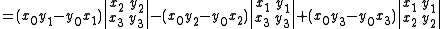
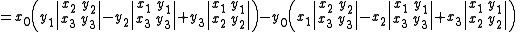
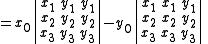
Since both 3×3 determinants have duplicate columns, the right hand side is identically zero.
Another proof may be done like this:
Since vector
is perpendicular to vector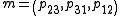
(see above), the scalar product of d and m must be zero! q.e.d.
Point equations
Letting (x0:x1:x2:x3) be the point coordinates, four possible points on a line each have coordinates xi = pij, for j = 0…3. Some of these possible points may be inadmissible because all coordinates are zero, but since at least one Plücker coordinate is nonzero, at least two distinct points are guaranteed.
Bijectivity
If (q01:q02:q03:q23:q31:q12) are the homogeneous coordinates of a point in P5, without loss of generality assume that q01 is nonzero. Then the matrix
has rank 2, and so its columns are distinct points defining a line L. When the P5 coordinates, qij, satisfy the quadratic Plücker relation, they are the Plücker coordinates of L. To see this, first normalize q01 to 1. Then we immediately have that for the Plücker coordinates computed from M, pij = qij, except for
But if the qij satisfy the Plücker relation q23+q02q31+q03q12 = 0, then p23 = q23, completing the set of identities.
Consequently, α is a surjection onto the algebraic varietyAlgebraic varietyIn mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
consisting of the set of zeros of the quadratic polynomial
And since α is also an injection, the lines in P3 are thus in bijectiveBijectionA bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
correspondence with the points of this quadricQuadricIn mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
in P5, called the Plücker quadric or Klein quadricKlein quadricThe lines of a 3-dimensional projective space, S, can be viewed as points of a 5-dimensional projective space, T. In that 5-space, the points that represent a line in S lie on a hyperbolic quadric, Q known as the Klein quadric....
.
Uses
Plücker coordinates allow concise solutions to problems of line geometry in 3-dimensional space, especially those involving incidenceIncidence (geometry)In geometry, the relations of incidence are those such as 'lies on' between points and lines , and 'intersects' . That is, they are the binary relations describing how subsets meet...
.
Line-line crossing
Two lines in P3 are either skewSkew linesIn solid geometry, skew lines are two lines that do not intersect and are not parallel. Equivalently, they are lines that are not coplanar. A simple example of a pair of skew lines is the pair of lines through opposite edges of a regular tetrahedron...
or coplanar, and in the latter case they are either coincident or intersect in a unique point. If pij and p′ij are the Plücker coordinates of two lines, then they are coplanar precisely when d⋅m′+m⋅d′ = 0, as shown by
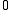
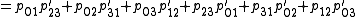

When the lines are skew, the sign of the result indicates the sense of crossing: positive if a right-handed screw takes L into L′, else negative.
The quadratic Plücker relation essentially states that a line is coplanar with itself.
Line-line join
In the event that two lines are coplanar but not parallel, their common plane has equation
- 0 = (m•d′)x0 + (d×d′)•x ,
where x = (x1,x2,x3).
The slightest perturbation will destroy the existence of a common plane, and near-parallelism of the lines will cause numeric difficulties in finding such a plane even if it does exist.
Line-line meet
Dually, two coplanar lines, neither of which contains the origin, have common point
- (x0 : x) = (d•m′:m×m′) .
To handle lines not meeting this restriction, see the references.
Plane-line meet
Given a plane with equation
or more concisely 0 = a0x0+a•x; and given a line not in it with Plücker coordinates (d:m), then their point of intersection is
- (x0 : x) = (a•d : a×m − a0d) .
The point coordinates, (x0:x1:x2:x3), can also be expressed in terms of Plücker coordinates as
Point-line join
Dually, given a point (y0:y) and a line not containing it, their common plane has equation
- 0 = (y•m) x0 + (y×d−y0m)•x .
The plane coordinates, (a0:a1:a2:a3), can also be expressed in terms of dual Plücker coordinates as
Line families
Because the Klein quadricKlein quadricThe lines of a 3-dimensional projective space, S, can be viewed as points of a 5-dimensional projective space, T. In that 5-space, the points that represent a line in S lie on a hyperbolic quadric, Q known as the Klein quadric....
is in P5, it contains linear subspaces of dimensions one and two (but no higher). These correspond to one- and two-parameter families of lines in P3.
For example, suppose L and L′ are distinct lines in P3 determined by points x, y and x′, y′, respectively. Linear combinations of their determining points give linear combinations of their Plücker coordinates, generating a one-parameter family of lines containing L and L′. This corresponds to a one-dimensional linear subspace belonging to the Klein quadric.
Lines in plane
If three distinct and non-parallel lines are coplanar; their linear combinations generate a two-parameter family of lines, all the lines in the plane. This corresponds to a two-dimensional linear subspace belonging to the Klein quadric.
Lines through point
If three distinct and non-coplanar lines intersect in a point, their linear combinations generate a two-parameter family of lines, all the lines through the point. This also corresponds to a two-dimensional linear subspace belonging to the Klein quadric.
Ruled surface
A ruled surfaceRuled surfaceIn geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
is a family of lines that is not necessarily linear. It corresponds to a curve on the Klein quadric. For example, a hyperboloid of one sheet is a quadric surface in P3 ruled by two different families of lines, one line of each passing through each point of the surface; each family corresponds under the Plücker map to a conic sectionConic sectionIn mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
within the Klein quadric in P5.
Line geometry
During the nineteenth century, line geometry was studied intensively. In terms of the bijection given above, this is a description of the intrinsic geometry of the Klein quadric.
Ray tracing
Line geometry is extensively used in ray tracing application where the geometry and intersections of rays need to be calculated in 3D. An implementation is described in
Introduction to Pluecker Coordinates written for the Ray Tracing forum by Thouis Jones. -