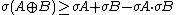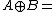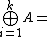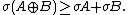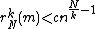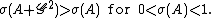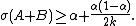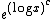Schnirelmann density
Encyclopedia
In additive number theory
, the Schnirelmann density of a sequence
of numbers is a way to measure how "dense" the sequence is. It is named after Russia
n mathematician
L.G. Schnirelmann, who was the first to study it.
s A is defined as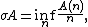
where A(n) denotes the number of elements of A not exceeding n and inf is infimum
.
The Schnirelmann density is well-defined even if the limit of A(n)/n as fails to exist (see asymptotic density).
In particular,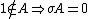
and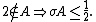
Consequently, the Schnirelmann densities of the even numbers and the odd numbers, which one might expect to agree, are 0 and 1/2 respectively. Schnirelmann and Yuri Linnik
exploited this sensitivity as we shall see.
, then Lagrange's four-square theorem
can be restated as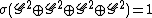
. (Here the symbol 
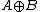denotes the sumset
of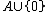
and 
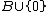.) It is clear that 
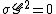. In fact, we still have 
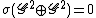, and one might ask at what point the sumset attains Schnirelmann density 1 and how does it increase. It actually is the case that 
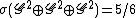and one sees that sumsetting 
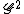once again yields a more populous set, namely all of . Schnirelmann further succeeded in developing these ideas into the following theorems, aiming towards Additive Number Theory, and proving them to be a novel resource (if not greatly powerful) to attack important problems, such as Waring's problem and Goldbach's conjecture.
Note that
. Inductively, we have the following generalization.
The theorem provides the first insights on how sumsets accumulate. It seems unfortunate that its conclusion stops short of showing
being superadditive. Yet, Schnirelmann provided us with the following results, which sufficed for most of his purpose.
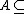with the property that 
for a finite sum, is called an additive basis, and the least number of summands required is called the degree (sometimes order) of the basis. Thus, the last theorem states that any set with positive Schnirelmann density is an additive basis. In this terminology, the set of squares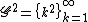 
is an additive basis of degree 4.
hypothesis. It was used by Edmund Landau
and was finally proved by Henry Mann
in 1942.
and 
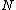be natural numbers. Let 
. Define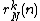 
to be the number of non-negative integral solutions to the equation
and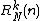
to be the number of non-negative integral solutions to the inequality
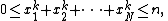
in the variables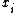
, respectively. Thus 
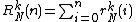. We have
The volume of the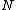
-dimensional body defined by 
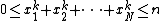, is bounded by the volume of the hypercube of size 
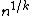, hence 
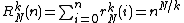. The hard part is to show that this bound still works on the average, i.e.,
With this at hand, the following theorem can be elegantly proved.
We have thus established the general solution to Waring's Problem:
to prove Schnirelmann's theorem, that any natural number
greater than one can be written as the sum of not more than C prime numbers, where C is an effectively computable constant. Schnirelmann's constant is the lowest number C with this property.
Olivier Ramaré
showed in that Schnirelmann's constant is at most 7, improving the earlier upper bound 19 by Hans Riesel
and R. C. Vaughan.
Schnirelmann's constant is at least 3; Goldbach's conjecture
implies that this is the constant's actual value.
This was soon simplified and extended by Erdős
, who showed, that if A is any sequence with Schnirelmann density α and B is an additive basis of order k then
Sequences with this property were named essential components by Khintchin. Linnik
showed that an essential component need not be an additive basis as he constructed an essential component that has xo(1) elements less than x. More precisely, the sequence has
elements less than x for some c < 1. This was improved by E. Wirsing to
For a while, it remained an open problem how many elements an essential component must have. Finally, Ruzsa
determined that an essential component has at least (log x)c elements up to x, for some c > 1, and for every c > 1 there is an essential component which has at most (log x)c elements up to x.
Additive number theory
In number theory, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian groups and commutative semigroups with an operation of addition. Additive number theory has...
, the Schnirelmann density of a sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
of numbers is a way to measure how "dense" the sequence is. It is named after Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
L.G. Schnirelmann, who was the first to study it.
Definition
The Schnirelmann density of a set of natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s A is defined as
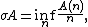
where A(n) denotes the number of elements of A not exceeding n and inf is infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
.
The Schnirelmann density is well-defined even if the limit of A(n)/n as fails to exist (see asymptotic density).
Properties
By definition, and for all n, and therefore , and σA = 1 if and only if A = N. Furthermore,
Sensitivity
The Schnirelmann density is sensitive to the first values of a set:-
.
In particular,
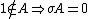
and
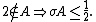
Consequently, the Schnirelmann densities of the even numbers and the odd numbers, which one might expect to agree, are 0 and 1/2 respectively. Schnirelmann and Yuri Linnik
Yuri Linnik
Yuri Vladimirovich Linnik was a Soviet mathematician active in number theory, probability theory and mathematical statistics.Linnik was born in Bila Tserkva, in present-day Ukraine. He went to St Petersburg University where his supervisor was Vladimir Tartakovski, and later worked at that...
exploited this sensitivity as we shall see.
Schnirelmann's theorems
If we set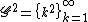, then Lagrange's four-square theoremLagrange's four-square theorem
Lagrange's four-square theorem, also known as Bachet's conjecture, states that any natural number can be represented as the sum of four integer squaresp = a_0^2 + a_1^2 + a_2^2 + a_3^2\ where the four numbers are integers...
can be restated as
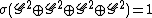. (Here the symbol 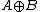denotes the sumsetSumset
In additive combinatorics, the sumset of two subsets A and B of an abelian group G is defined to be the set of all sums of an element from A with an element from B...
of
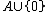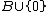and .) It is clear that 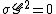. In fact, we still have 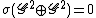, and one might ask at what point the sumset attains Schnirelmann density 1 and how does it increase. It actually is the case that 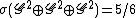and one sees that sumsetting 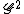once again yields a more populous set, namely all of . Schnirelmann further succeeded in developing these ideas into the following theorems, aiming towards Additive Number Theory, and proving them to be a novel resource (if not greatly powerful) to attack important problems, such as Waring's problem and Goldbach's conjecture.
Theorem. Letand
be subsets of . Then
Note that
. Inductively, we have the following generalization.
Corollary. Letbe a finite family of subsets of . Then
The theorem provides the first insights on how sumsets accumulate. It seems unfortunate that its conclusion stops short of showing
being superadditive. Yet, Schnirelmann provided us with the following results, which sufficed for most of his purpose.
Theorem. Letand
be subsets of . If
, then
Theorem. (Schnirelmann) Let. If
then there exists
such that
Additive bases
A subset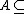 with the property that for a finite sum, is called an additive basis, and the least number of summands required is called the degree (sometimes order) of the basis. Thus, the last theorem states that any set with positive Schnirelmann density is an additive basis. In this terminology, the set of squares 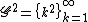is an additive basis of degree 4.Mann's theorem
Historically the theorems above were pointers to the following result, at one time known as the hypothesis. It was used by Edmund LandauEdmund Landau
Edmund Georg Hermann Landau was a German Jewish mathematician who worked in the fields of number theory and complex analysis.-Biography:...
and was finally proved by Henry Mann
Henry Mann
Henry Berthold Mann was a professor of mathematics and statistics at Ohio State University. Mann proved the Schnirelmann-Landau conjecture in number theory, and as a result earned the 1946 Cole Prize. He and his student developed the U-statistic of nonparametric statistics...
in 1942.
Theorem. Letand
be subsets of . In case that
, we still have
Waring's problem
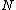Let and be natural numbers. Let . Define 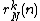to be the number of non-negative integral solutions to the equationand
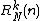to be the number of non-negative integral solutions to the inequality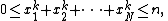in the variables
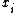, respectively. Thus 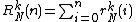. We have
The volume of the
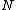-dimensional body defined by 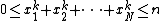, is bounded by the volume of the hypercube of size 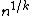, hence 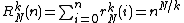. The hard part is to show that this bound still works on the average, i.e.,
Lemma. (Linnik) For allthere exists
and a constant
, depending only on
, such that for all
,
for all
With this at hand, the following theorem can be elegantly proved.
Theorem. For allthere exists
for which
.
We have thus established the general solution to Waring's Problem:
Corollary. For allthere exists
, depending only on
, such that every positive integer
can be expressed as the sum of at most
many
-th powers.
Schnirelmann's theorem
In 1931 Schnirelmann used these ideas in conjunction with the Brun sieveBrun sieve
In the field of number theory, the Brun sieve is a technique for estimating the size of "sifted sets" of positive integers which satisfy a set of conditions which are expressed by congruences...
to prove Schnirelmann's theorem, that any natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
greater than one can be written as the sum of not more than C prime numbers, where C is an effectively computable constant. Schnirelmann's constant is the lowest number C with this property.
Olivier Ramaré
Olivier Ramaré
Olivier Ramaré is a French mathematician who teaches at the Université des Sciences et Technologies de Lille.In 1995, he sharpened earlier work on Schnirelmann's theorem by proving that every even number is a sum of at most six primes. This result may be compared with Goldbach's conjecture, which...
showed in that Schnirelmann's constant is at most 7, improving the earlier upper bound 19 by Hans Riesel
Hans Riesel
Hans Ivar Riesel is a Swedish mathematician who discovered the 18th known Mersenne prime in 1957, using the computer BESK. This prime is 23217-1, which consists of 969 digits. He held the record for the largest known prime from 1957 to 1961, when Alexander Hurwitz discovered a larger one. Riesel...
and R. C. Vaughan.
Schnirelmann's constant is at least 3; Goldbach's conjecture
Goldbach's conjecture
Goldbach's conjecture is one of the oldest unsolved problems in number theory and in all of mathematics. It states:A Goldbach number is a number that can be expressed as the sum of two odd primes...
implies that this is the constant's actual value.
Essential components
Khintchin proved that the sequence of squares, though of zero Schnirelmann density, when added to a sequence of Schnirelmann density between 0 and 1, increases the density:
This was soon simplified and extended by Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
, who showed, that if A is any sequence with Schnirelmann density α and B is an additive basis of order k then
Sequences with this property were named essential components by Khintchin. Linnik
Yuri Linnik
Yuri Vladimirovich Linnik was a Soviet mathematician active in number theory, probability theory and mathematical statistics.Linnik was born in Bila Tserkva, in present-day Ukraine. He went to St Petersburg University where his supervisor was Vladimir Tartakovski, and later worked at that...
showed that an essential component need not be an additive basis as he constructed an essential component that has xo(1) elements less than x. More precisely, the sequence has
elements less than x for some c < 1. This was improved by E. Wirsing to
For a while, it remained an open problem how many elements an essential component must have. Finally, Ruzsa
Imre Z. Ruzsa
Imre Z. Ruzsa is a Hungarian mathematician specializing in number theory.Ruzsa participated in the International Mathematical Olympiad for Hungary, winning a silver medal in 1969, and two consecutive gold medals with perfect scores in 1970 and 1971. He graduated from the Eötvös Loránd University...
determined that an essential component has at least (log x)c elements up to x, for some c > 1, and for every c > 1 there is an essential component which has at most (log x)c elements up to x.