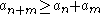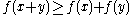Superadditive
Encyclopedia
In mathematics, a sequence
{ an }, n ≥ 1, is called superadditive if it satisfies the inequality
for all m and n. The major reason for the use of superadditive sequences is the following lemma
due to Michael Fekete.
Lemma: (Fekete) For every superadditive sequence { an }, n ≥ 1, the limit lim an/n exists and equal to sup an/n. (The limit may be positive infinity, for instance, for the sequence an = log n! .)
Similarly, a function
f(x) is superadditive if
for all x and y in the domain
of f.
For example,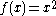
is a superadditive function for nonnegative real numbers because the square of 
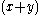is always greater than or equal to the square of 
plus the square of 
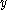, for nonnegative real numbers 
and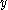 
.
The analogue of Fekete's lemma holds for subadditive functions as well.
There are extensions of Fekete's lemma that do not require the definition of superadditivity above to hold for all m and n. There are also results that allow one to deduce the rate of convergence to the limit whose existence is stated in Fekete's lemma if some kind of both superadditivity and subadditivity is present. A good exposition of this topic may be found in Steele (1997).
If f is a superadditive function, and if 0 is in its domain, then f(0) ≤ 0. To see this, take the inequality at the top.
. Hence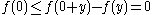 
The negative of a superadditive function is subadditive.
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
{ an }, n ≥ 1, is called superadditive if it satisfies the inequality
for all m and n. The major reason for the use of superadditive sequences is the following lemma
Lemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
due to Michael Fekete.
Lemma: (Fekete) For every superadditive sequence { an }, n ≥ 1, the limit lim an/n exists and equal to sup an/n. (The limit may be positive infinity, for instance, for the sequence an = log n
Similarly, a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f(x) is superadditive if
for all x and y in the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
of f.
For example,
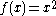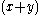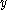is a superadditive function for nonnegative real numbers because the square of is always greater than or equal to the square of plus the square of , for nonnegative real numbers and 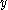.The analogue of Fekete's lemma holds for subadditive functions as well.
There are extensions of Fekete's lemma that do not require the definition of superadditivity above to hold for all m and n. There are also results that allow one to deduce the rate of convergence to the limit whose existence is stated in Fekete's lemma if some kind of both superadditivity and subadditivity is present. A good exposition of this topic may be found in Steele (1997).
If f is a superadditive function, and if 0 is in its domain, then f(0) ≤ 0. To see this, take the inequality at the top.
. Hence 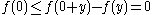The negative of a superadditive function is subadditive.
Examples of superadditive functions
- Mutual informationMutual informationIn probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
- Horst Alzer proved that Hadamard’s gamma function H(x) is superadditive for all real numbers x,y with x, y ≥ 1.5031.