
Additive number theory
Encyclopedia
In number theory
, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian group
s and commutative semigroups with an operation of addition. Additive number theory has close ties to combinatorial number theory and the geometry of numbers
. Two principal objects of study are the sumset
of two subsets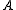 and
and 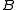 of elements from an Abelian group
of elements from an Abelian group 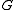 ,
,
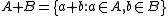 ,
,
and the h-fold sumset of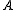 ,
,
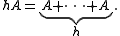
There are two main subdivisions listed below.
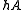 , where
, where 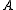 is a fixed subset. Two classical problems of this type are the Goldbach conjecture (which is the conjecture that
is a fixed subset. Two classical problems of this type are the Goldbach conjecture (which is the conjecture that 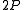 contains all even numbers greater than two, where
contains all even numbers greater than two, where 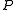 is the set of primes
is the set of primes
) and Waring's problem
(which asks how large must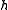 be to guarantee that
be to guarantee that 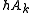 contains all positive integers, where
contains all positive integers, where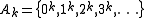
is the set of k-th powers). Many of these problems are studied using the tools from the Hardy-Littlewood circle method
and from sieve methods. For example, Vinogradov proved that every sufficiently large odd number is the sum of three primes, and so every sufficiently large even integer is the sum of four primes. Hilbert proved that, for every integer k > 1, every nonnegative integer is the sum of a bounded number of k-th powers. In general, a set A of nonnegative integers is called a basis of order h if contains all positive integers, and it is called an assymptotic basis if
contains all positive integers, and it is called an assymptotic basis if 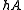 contains all sufficiently large integers. Much current research in this area concerns properties of general asymptotic bases of finite order. For example, a set A is called a minimal asymptotic basis of order h if A is an asymptotic basis of order h but no proper subset of A is an asymptotic basis of order h. It has been proved that minimal asymptotic bases of order h exist for all h, and that there also exist asymptotic bases of order h that contain no minimal asymptotic bases of order h. Another question to be considered is how small can the number of representations of
contains all sufficiently large integers. Much current research in this area concerns properties of general asymptotic bases of finite order. For example, a set A is called a minimal asymptotic basis of order h if A is an asymptotic basis of order h but no proper subset of A is an asymptotic basis of order h. It has been proved that minimal asymptotic bases of order h exist for all h, and that there also exist asymptotic bases of order h that contain no minimal asymptotic bases of order h. Another question to be considered is how small can the number of representations of  as a sum of
as a sum of 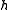 elements in an asymptotic basis can be. This is the content of the Erdős–Turán conjecture on additive bases
elements in an asymptotic basis can be. This is the content of the Erdős–Turán conjecture on additive bases
.
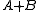 , the aim is find information about the structure of the individual sets
, the aim is find information about the structure of the individual sets 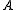 and
and 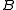 . (A more recent name sometimes associated to this sub-division is additive combinatorics.) Unlike problems related to classical bases, as described above, this sub-area often deals with finite subsets rather than infinite ones. A typical question is what is the structure of a pair of subsets whose sumset has small cardinality (in relation to
. (A more recent name sometimes associated to this sub-division is additive combinatorics.) Unlike problems related to classical bases, as described above, this sub-area often deals with finite subsets rather than infinite ones. A typical question is what is the structure of a pair of subsets whose sumset has small cardinality (in relation to 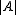 and
and 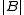 ). In the case of the integers, the classical Freiman's theorem
). In the case of the integers, the classical Freiman's theorem
provides a potent partial answer to this question in terms of multi-dimensional arithmetic progressions. Another typical problem is simply to find a lower bound for in terms of
in terms of 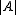 and
and  (this can be view as an inverse problem with the given information for
(this can be view as an inverse problem with the given information for 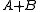 being that
being that 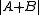 is sufficiently small and the structural conclusion then being that that either
is sufficiently small and the structural conclusion then being that that either  or
or  is the empty set; such problems are often considered direct problems as well). Examples of this type include the Erdős–Heilbronn Conjecture (for a restricted sumset) and the Cauchy-Davenport Theorem. The methods used for tackling such questions draw from across the spectrum of mathematics, including combinatorics, ergodic theory
is the empty set; such problems are often considered direct problems as well). Examples of this type include the Erdős–Heilbronn Conjecture (for a restricted sumset) and the Cauchy-Davenport Theorem. The methods used for tackling such questions draw from across the spectrum of mathematics, including combinatorics, ergodic theory
, analysis
, graph theory
, group theory
, and linear algebraic and polynomial methods.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the specialty additive number theory studies subsets of integers and their behavior under addition. More abstractly, the field of "additive number theory" includes the study of Abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s and commutative semigroups with an operation of addition. Additive number theory has close ties to combinatorial number theory and the geometry of numbers
Geometry of numbers
In number theory, the geometry of numbers studies convex bodies and integer vectors in n-dimensional space. The geometry of numbers was initiated by ....
. Two principal objects of study are the sumset
Sumset
In additive combinatorics, the sumset of two subsets A and B of an abelian group G is defined to be the set of all sums of an element from A with an element from B...
of two subsets
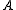 and
and 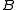 of elements from an Abelian group
of elements from an Abelian group 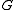 ,
,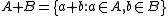 ,
,and the h-fold sumset of
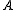 ,
,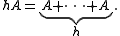
There are two main subdivisions listed below.
Additive number theory
The first is principally devoted to consideration of direct problems over (typically) the integers, that is, to determining which elements can be represented as a summand from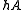 , where
, where 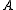 is a fixed subset. Two classical problems of this type are the Goldbach conjecture (which is the conjecture that
is a fixed subset. Two classical problems of this type are the Goldbach conjecture (which is the conjecture that 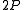 contains all even numbers greater than two, where
contains all even numbers greater than two, where 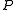 is the set of primes
is the set of primesPrime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
) and Waring's problem
Waring's problem
In number theory, Waring's problem, proposed in 1770 by Edward Waring, asks whether for every natural number k there exists an associated positive integer s such that every natural number is the sum of at most s kth powers of natural numbers...
(which asks how large must
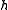 be to guarantee that
be to guarantee that 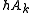 contains all positive integers, where
contains all positive integers, where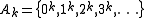
is the set of k-th powers). Many of these problems are studied using the tools from the Hardy-Littlewood circle method
Hardy-Littlewood circle method
In mathematics, the Hardy–Littlewood circle method is one of the most frequently used techniques of analytic number theory. It is named for G. H. Hardy and J. E...
and from sieve methods. For example, Vinogradov proved that every sufficiently large odd number is the sum of three primes, and so every sufficiently large even integer is the sum of four primes. Hilbert proved that, for every integer k > 1, every nonnegative integer is the sum of a bounded number of k-th powers. In general, a set A of nonnegative integers is called a basis of order h if
 contains all positive integers, and it is called an assymptotic basis if
contains all positive integers, and it is called an assymptotic basis if 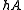 contains all sufficiently large integers. Much current research in this area concerns properties of general asymptotic bases of finite order. For example, a set A is called a minimal asymptotic basis of order h if A is an asymptotic basis of order h but no proper subset of A is an asymptotic basis of order h. It has been proved that minimal asymptotic bases of order h exist for all h, and that there also exist asymptotic bases of order h that contain no minimal asymptotic bases of order h. Another question to be considered is how small can the number of representations of
contains all sufficiently large integers. Much current research in this area concerns properties of general asymptotic bases of finite order. For example, a set A is called a minimal asymptotic basis of order h if A is an asymptotic basis of order h but no proper subset of A is an asymptotic basis of order h. It has been proved that minimal asymptotic bases of order h exist for all h, and that there also exist asymptotic bases of order h that contain no minimal asymptotic bases of order h. Another question to be considered is how small can the number of representations of  as a sum of
as a sum of 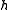 elements in an asymptotic basis can be. This is the content of the Erdős–Turán conjecture on additive bases
elements in an asymptotic basis can be. This is the content of the Erdős–Turán conjecture on additive basesErdős–Turán conjecture on additive bases
The Erdős–Turán conjecture is an old unsolved problem in additive number theory posed by Paul Erdős and Pál Turán in 1941.-History:...
.
Additive combinatorics
The second is principally devoted to consideration of inverse problems, often over more general groups than just the integers, that is, given some information about the sumset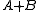 , the aim is find information about the structure of the individual sets
, the aim is find information about the structure of the individual sets 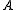 and
and 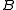 . (A more recent name sometimes associated to this sub-division is additive combinatorics.) Unlike problems related to classical bases, as described above, this sub-area often deals with finite subsets rather than infinite ones. A typical question is what is the structure of a pair of subsets whose sumset has small cardinality (in relation to
. (A more recent name sometimes associated to this sub-division is additive combinatorics.) Unlike problems related to classical bases, as described above, this sub-area often deals with finite subsets rather than infinite ones. A typical question is what is the structure of a pair of subsets whose sumset has small cardinality (in relation to 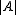 and
and 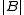 ). In the case of the integers, the classical Freiman's theorem
). In the case of the integers, the classical Freiman's theoremFreiman's theorem
In mathematics, Freiman's theorem is a combinatorial result in number theory. In a sense it accounts for the approximate structure of sets of integers that contain a high proportion of their internal sums, taken two at a time.The formal statement is:...
provides a potent partial answer to this question in terms of multi-dimensional arithmetic progressions. Another typical problem is simply to find a lower bound for
 in terms of
in terms of 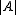 and
and  (this can be view as an inverse problem with the given information for
(this can be view as an inverse problem with the given information for 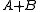 being that
being that 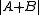 is sufficiently small and the structural conclusion then being that that either
is sufficiently small and the structural conclusion then being that that either  or
or  is the empty set; such problems are often considered direct problems as well). Examples of this type include the Erdős–Heilbronn Conjecture (for a restricted sumset) and the Cauchy-Davenport Theorem. The methods used for tackling such questions draw from across the spectrum of mathematics, including combinatorics, ergodic theory
is the empty set; such problems are often considered direct problems as well). Examples of this type include the Erdős–Heilbronn Conjecture (for a restricted sumset) and the Cauchy-Davenport Theorem. The methods used for tackling such questions draw from across the spectrum of mathematics, including combinatorics, ergodic theoryErgodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
, analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
, graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, and linear algebraic and polynomial methods.

