
Brun sieve
Encyclopedia
In the field of number theory
, the Brun sieve (also called Brun's pure sieve) is a technique for estimating the size of "sifted sets" of positive integers which satisfy a set of conditions which are expressed by congruences. It was developed by Viggo Brun
in 1915.
the Brun sieve is of combinatorial type: that is, derives from a careful use of the inclusion-exclusion principle
.
Let A be a set of positive integers ≤ x and let P be a set of primes. For each p in P, let Ap denote the set of elements of A divisible by p and extend this to let Ad the intersection of the Ap for p dividing d, when d is a product of distinct primes from P. Further let A1 denote A itself. Let z be a positive real number and P(z) denote the primes in P ≤ z. The object of the sieve is to estimate

We assume that |Ad| may be estimated by
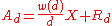
where w is a multiplicative function
and X = |A|. Let

where C, D, E are constants.
Then

In particular, if log z < c log x / log log x for a suitably small c, then
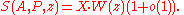
The last two results were superseded by Chen's theorem
.
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Brun sieve (also called Brun's pure sieve) is a technique for estimating the size of "sifted sets" of positive integers which satisfy a set of conditions which are expressed by congruences. It was developed by Viggo Brun
Viggo Brun
Viggo Brun was a Norwegian mathematician.He studied at the University of Oslo and began research at the University of Göttingen in 1910. In 1923, Brun became a professor at the Technical University in Trondheim and in 1946 a professor at the University of Oslo...
in 1915.
Description
In terms of sieve theorySieve theory
Sieve theory is a set of general techniques in number theory, designed to count, or more realistically to estimate the size of, sifted sets of integers. The primordial example of a sifted set is the set of prime numbers up to some prescribed limit X. Correspondingly, the primordial example of a...
the Brun sieve is of combinatorial type: that is, derives from a careful use of the inclusion-exclusion principle
Inclusion-exclusion principle
In combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
.
Let A be a set of positive integers ≤ x and let P be a set of primes. For each p in P, let Ap denote the set of elements of A divisible by p and extend this to let Ad the intersection of the Ap for p dividing d, when d is a product of distinct primes from P. Further let A1 denote A itself. Let z be a positive real number and P(z) denote the primes in P ≤ z. The object of the sieve is to estimate

We assume that |Ad| may be estimated by
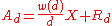
where w is a multiplicative function
Multiplicative function
In number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
and X = |A|. Let

Brun's pure sieve
This formulation is from Cocojaru & Murty, Theorem 6.1.2. With the notation as above, assume that- |Rd| ≤ w(d) for any squarefree d composed of primes in P ;
- w(p) < C for all p in P ;
-

where C, D, E are constants.
Then

In particular, if log z < c log x / log log x for a suitably small c, then
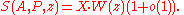
Applications
- Brun's theoremBrun's theoremIn number theory, Brun's theorem was proved by Viggo Brun in 1919. It states that the sum of the reciprocals of the twin primes is convergent with a finite value known as Brun's constant, usually denoted by B2...
: the sum of the reciprocals of the twin primeTwin primeA twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
s converges; - Schnirelmann's theorem: every even number is a sum of at most C primes (where C can be taken to be 6);
- There are infinitely many pairs of integers differing by 2, where each of the member of the pair is the product of at most 9 primes;
- Every even number is the sum of two numbers each of which is the product of at most 9 primes.
The last two results were superseded by Chen's theorem
Chen's theorem
right|thumb|Chen JingrunChen's theorem states that every sufficiently large even number can be written as the sum of either two primes, or a prime and a semiprime . The theorem was first stated by Chinese mathematician Chen Jingrun in 1966, with further details of the proof in 1973. His original...
.

