Rotational diffusion
Encyclopedia
Rotational diffusion is a process by which the equilibrium
statistical distribution of the overall orientation of particles or molecules is maintained or restored. Rotational diffusion is the counterpart of translational diffusion, which maintains or restores the equilibrium statistical distribution of particles' position in space.
The random re-orientation of molecules (or larger systems) is an important process for many biophysical
probes. Due to the equipartition theorem
, larger molecules re-orient more slowly than do smaller objects and, hence, measurements of the rotational diffusion constants can give insight into the overall mass and its distribution within an object. Quantitatively, the mean square of the angular velocity
about each of an object's principal axes is inversely proportional to its moment of inertia
about that axis. Therefore, there should be three rotational diffusion constants - the eigenvalues of the rotational diffusion tensor - resulting in five rotational time constant
s . If two eigenvalues of the diffusion tensor are equal, the particle diffuses as a spheroid
with two unique diffusion rates and three time constants. And if all eigenvalues are the same, the particle diffuses as a sphere
with one time constant. The diffusion tensor may be determined from the Perrin friction factors
, in analogy with the Einstein relation
of translational diffusion
, but often this is inaccurate and direct measurement is required.
The rotational diffusion tensor may be determined experimentally through fluorescence anisotropy
, flow birefringence
, dielectric spectroscopy
, NMR relaxation
and other biophysical methods sensitive to picosecond or slower rotational processes. In some techniques such as fluorescence it may be very difficult to characterize the full diffusion tensor, for example measuring two diffusion rates can sometimes be possible when there is a great difference between them, e.g., for very long, thin ellipsoids such as certain virus
es. This is however not the case of the extremely sensitive, atomic resolution technique of NMR relaxation that can be used to fully determine the rotational diffusion tensor to very high precision.
is
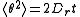
where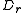
is the rotational diffusion coefficient (in units of radians2/s).
The angular drift velocity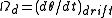
in response to an external torque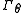 
(assuming that the flow stays non-turbulent and that inertial effects can be neglected) is given by
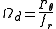
where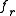
is the frictional drag coefficient. The relationship between the rotational diffusion coefficient and the rotational frictional drag coefficient is given by the Einstein relation
(or Einstein–Smoluchowski relation):
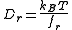
where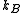
is the Boltzmann constant and 
is the absolute temperature.
These relationship are in complete analogy to translational diffusion.
The rotational frictional drag coefficient for a sphere of radiu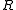s
is
where
is the dynamic viscosity.
can be defined. Let each rotating molecule be associated with a vector n of unit length n·n=1; for example, n might represent the orientation of an electric or magnetic dipole moment. Let f(θ, φ, t) represent the probability density distribution
for the orientation of n at time t. Here, θ and φ represent the spherical angles
, with θ being the polar angle between n and the z-axis and φ being the azimuthal angle of n in the x-y plane. The rotational version of Fick's law states
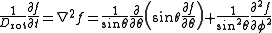
This partial differential equation
(PDE) may be solved by expanding f(θ, φ, t) in spherical harmonics
for which the mathematical identity holds
Thus, the solution of the PDE may be written
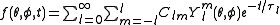
where Clm are constants fitted to the initial distribution and the time constants equal
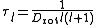
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
statistical distribution of the overall orientation of particles or molecules is maintained or restored. Rotational diffusion is the counterpart of translational diffusion, which maintains or restores the equilibrium statistical distribution of particles' position in space.
The random re-orientation of molecules (or larger systems) is an important process for many biophysical
Biophysics
Biophysics is an interdisciplinary science that uses the methods of physical science to study biological systems. Studies included under the branches of biophysics span all levels of biological organization, from the molecular scale to whole organisms and ecosystems...
probes. Due to the equipartition theorem
Equipartition theorem
In classical statistical mechanics, the equipartition theorem is a general formula that relates the temperature of a system with its average energies. The equipartition theorem is also known as the law of equipartition, equipartition of energy, or simply equipartition...
, larger molecules re-orient more slowly than do smaller objects and, hence, measurements of the rotational diffusion constants can give insight into the overall mass and its distribution within an object. Quantitatively, the mean square of the angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
about each of an object's principal axes is inversely proportional to its moment of inertia
Moment of inertia
In classical mechanics, moment of inertia, also called mass moment of inertia, rotational inertia, polar moment of inertia of mass, or the angular mass, is a measure of an object's resistance to changes to its rotation. It is the inertia of a rotating body with respect to its rotation...
about that axis. Therefore, there should be three rotational diffusion constants - the eigenvalues of the rotational diffusion tensor - resulting in five rotational time constant
Time constant
In physics and engineering, the time constant, usually denoted by the Greek letter \tau , is the risetime characterizing the response to a time-varying input of a first-order, linear time-invariant system.Concretely, a first-order LTI system is a system that can be modeled by a single first order...
s . If two eigenvalues of the diffusion tensor are equal, the particle diffuses as a spheroid
Spheroid
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....
with two unique diffusion rates and three time constants. And if all eigenvalues are the same, the particle diffuses as a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
with one time constant. The diffusion tensor may be determined from the Perrin friction factors
Perrin friction factors
In hydrodynamics, the Perrin friction factors are multiplicative adjustments to the translational and rotational friction of a rigid spheroid, relative to the corresponding frictions in spheres of the same volume...
, in analogy with the Einstein relation
Einstein relation (kinetic theory)
In physics the Einstein relation is a previously unexpected connection revealed independently by Albert Einstein in 1905 and by Marian Smoluchowski in their papers on Brownian motion...
of translational diffusion
Diffusion
Molecular diffusion, often called simply diffusion, is the thermal motion of all particles at temperatures above absolute zero. The rate of this movement is a function of temperature, viscosity of the fluid and the size of the particles...
, but often this is inaccurate and direct measurement is required.
The rotational diffusion tensor may be determined experimentally through fluorescence anisotropy
Fluorescence anisotropy
Fluorescence anisotropy is the phenomenon where the light emitted by a fluorophore has unequal intensities along different axes of polarization...
, flow birefringence
Flow birefringence
In biochemistry, flow birefringence is a hydrodynamic technique for measuring the rotational diffusion constants . The birefringence of a solution sandwiched between two concentric cylinders is measured as a function of the difference in rotational speed between the inner and outer cylinders...
, dielectric spectroscopy
Dielectric spectroscopy
Dielectric spectroscopy , and also known as electrochemical impedance spectroscopy, measures the dielectric properties of a medium as a function of frequency...
, NMR relaxation
Relaxation (NMR)
In nuclear magnetic resonance spectroscopy and magnetic resonance imaging the term relaxation describes several processes by which nuclear magnetization prepared in a non-equilibrium state return to the equilibrium distribution. In other words, relaxation describes how fast spins "forget" the...
and other biophysical methods sensitive to picosecond or slower rotational processes. In some techniques such as fluorescence it may be very difficult to characterize the full diffusion tensor, for example measuring two diffusion rates can sometimes be possible when there is a great difference between them, e.g., for very long, thin ellipsoids such as certain virus
Virus
A virus is a small infectious agent that can replicate only inside the living cells of organisms. Viruses infect all types of organisms, from animals and plants to bacteria and archaea...
es. This is however not the case of the extremely sensitive, atomic resolution technique of NMR relaxation that can be used to fully determine the rotational diffusion tensor to very high precision.
Basic equations of rotational diffusion
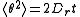
For rotational diffusion about a single axis, the mean-square angular deviation in time iswhere
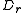is the rotational diffusion coefficient (in units of radians2/s).The angular drift velocity
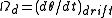in response to an external torque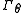 (assuming that the flow stays non-turbulent and that inertial effects can be neglected) is given by
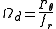
where
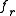is the frictional drag coefficient. The relationship between the rotational diffusion coefficient and the rotational frictional drag coefficient is given by the Einstein relationEinstein relation
Einstein relation can refer to*Einstein relation , a kinetic relation found independently by Albert Einstein and Marian Smoluchowski *Mass–energy equivalence, sometimes called Einstein's mass-energy relation...
(or Einstein–Smoluchowski relation):
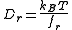
where
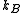is the Boltzmann constant and is the absolute temperature.These relationship are in complete analogy to translational diffusion.
The rotational frictional drag coefficient for a sphere of radius
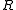iswhere
is the dynamic viscosity.Rotational version of Fick's law
A rotational version of Fick's law of diffusionFick's law of diffusion
Fick's laws of diffusion describe diffusion and can be used to solve for the diffusion coefficient, D. They were derived by Adolf Fick in the year 1855.- Fick's first law :...
can be defined. Let each rotating molecule be associated with a vector n of unit length n·n=1; for example, n might represent the orientation of an electric or magnetic dipole moment. Let f(θ, φ, t) represent the probability density distribution
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
for the orientation of n at time t. Here, θ and φ represent the spherical angles
Spherical coordinate system
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its inclination angle measured from a fixed zenith direction, and the azimuth angle of...
, with θ being the polar angle between n and the z-axis and φ being the azimuthal angle of n in the x-y plane. The rotational version of Fick's law states
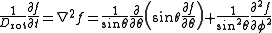
This partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
(PDE) may be solved by expanding f(θ, φ, t) in spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
for which the mathematical identity holds
Thus, the solution of the PDE may be written
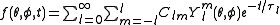
where Clm are constants fitted to the initial distribution and the time constants equal
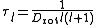
See also
- Diffusion equation
- Perrin friction factorsPerrin friction factorsIn hydrodynamics, the Perrin friction factors are multiplicative adjustments to the translational and rotational friction of a rigid spheroid, relative to the corresponding frictions in spheres of the same volume...
- Rotational diffusion tensor