
Perrin friction factors
Encyclopedia
In hydrodynamics, the Perrin friction factors are multiplicative adjustments to the translational and rotational friction of a rigid spheroid, relative to the corresponding frictions in spheres of the same volume. These friction factors were first calculated by Jean-Baptiste Perrin.
These factors pertain to spheroid
s (i.e., to ellipsoids of revolution), which are characterized by the axial ratio
p = (a/b), defined here as the axial semiaxis a
(i.e., the semiaxis along the axis of revolution) divided by the equatorial semiaxis b. In prolate spheroid
s, the axial ratio p > 1 since the axial semiaxis is longer than the equatorial semiaxes. Conversely, in oblate spheroids, the axial ratio p < 1 since the axial semiaxis is shorter than the equatorial semiaxes. Finally, in sphere
s, the axial ratio p = 1, since all three semiaxes are equal in length.
The formulae presented below assume "stick" (not "slip") boundary conditions, i.e., it is assumed that the velocity of the fluid is zero at the surface of the spheroid.
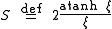
where the parameter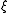 is defined
is defined
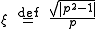
Similarly, for oblate spheroids (i.e., discus-shaped spheroids with two long axes and one short axis)
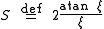
For spheres,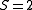 , as may be shown by taking the limit
, as may be shown by taking the limit 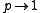 for the prolate or oblate spheroids.
for the prolate or oblate spheroids.
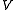 equals
equals
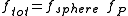
where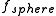 is the translational friction coefficient of a sphere of equivalent volume (Stokes' law
is the translational friction coefficient of a sphere of equivalent volume (Stokes' law
)
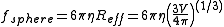
and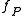 is the Perrin translational friction factor
is the Perrin translational friction factor
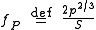
The frictional coefficient is related to the diffusion constant D by the Einstein relation
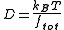
Hence, can be measured directly using analytical ultracentrifugation
can be measured directly using analytical ultracentrifugation
, or indirectly using various methods to determine the diffusion constant (e.g., NMR
and dynamic light scattering
).
 ) and other for a rotation about one of the equatorial semiaxes (denoted
) and other for a rotation about one of the equatorial semiaxes (denoted 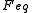 ).
).
Perrin
showed that
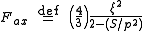
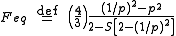
for both prolate and oblate spheroids. For spheres,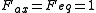 , as may be seen by taking the limit
, as may be seen by taking the limit 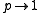 .
.
These formulae may be numerically unstable when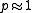 , since the numerator and denominator both go to zero into the
, since the numerator and denominator both go to zero into the 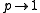 limit. In such cases, it may be better to expand in a series, e.g.,
limit. In such cases, it may be better to expand in a series, e.g.,
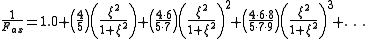
for oblate spheroids.

whereas that for the equatorial direction vectors is
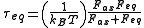
These time constants can differ significantly when the axial ratio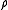 deviates significantly from 1, especially for prolate spheroids. Experimental methods for measuring these time constants include fluorescence anisotropy
deviates significantly from 1, especially for prolate spheroids. Experimental methods for measuring these time constants include fluorescence anisotropy
, NMR
, flow birefringence
and dielectric spectroscopy
.
It may seem paradoxical that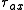 involves
involves 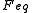 . This arises because re-orientations of the axial direction vector occur through rotations about the perpendicular axes, i.e., about the equatorial axes. Similar reasoning pertains to
. This arises because re-orientations of the axial direction vector occur through rotations about the perpendicular axes, i.e., about the equatorial axes. Similar reasoning pertains to  .
.
These factors pertain to spheroid
Spheroid
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....
s (i.e., to ellipsoids of revolution), which are characterized by the axial ratio
Axial ratio
Axial ratio, for any structure or shape with two or more axes, is the ratio of the length of those axes to each other - the longer axis divided by the shorter....
p = (a/b), defined here as the axial semiaxis a
(i.e., the semiaxis along the axis of revolution) divided by the equatorial semiaxis b. In prolate spheroid
Prolate spheroid
A prolate spheroid is a spheroid in which the polar axis is greater than the equatorial diameter. Prolate spheroids stand in contrast to oblate spheroids...
s, the axial ratio p > 1 since the axial semiaxis is longer than the equatorial semiaxes. Conversely, in oblate spheroids, the axial ratio p < 1 since the axial semiaxis is shorter than the equatorial semiaxes. Finally, in sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
s, the axial ratio p = 1, since all three semiaxes are equal in length.
The formulae presented below assume "stick" (not "slip") boundary conditions, i.e., it is assumed that the velocity of the fluid is zero at the surface of the spheroid.
Perrin S factor
For brevity in the equations below, we define the Perrin S factor. For prolate spheroids (i.e., cigar-shaped spheroids with two short axes and one long axis)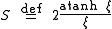
where the parameter
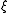 is defined
is defined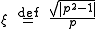
Similarly, for oblate spheroids (i.e., discus-shaped spheroids with two long axes and one short axis)
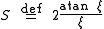
For spheres,
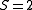 , as may be shown by taking the limit
, as may be shown by taking the limit 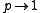 for the prolate or oblate spheroids.
for the prolate or oblate spheroids.Translational friction factor
The frictional coefficient of an arbitrary spheroid of volume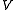 equals
equals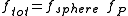
where
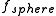 is the translational friction coefficient of a sphere of equivalent volume (Stokes' law
is the translational friction coefficient of a sphere of equivalent volume (Stokes' lawStokes' law
In 1851, George Gabriel Stokes derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a continuous viscous fluid...
)
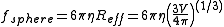
and
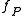 is the Perrin translational friction factor
is the Perrin translational friction factor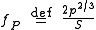
The frictional coefficient is related to the diffusion constant D by the Einstein relation
Einstein relation
Einstein relation can refer to*Einstein relation , a kinetic relation found independently by Albert Einstein and Marian Smoluchowski *Mass–energy equivalence, sometimes called Einstein's mass-energy relation...
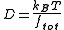
Hence,
 can be measured directly using analytical ultracentrifugation
can be measured directly using analytical ultracentrifugationUltracentrifuge
The ultracentrifuge is a centrifuge optimized for spinning a rotor at very high speeds, capable of generating acceleration as high as 2,000,000 g . There are two kinds of ultracentrifuges, the preparative and the analytical ultracentrifuge...
, or indirectly using various methods to determine the diffusion constant (e.g., NMR
NMR
NMR may refer to:Applications of Nuclear Magnetic Resonance:* Nuclear magnetic resonance* NMR spectroscopy* Solid-state nuclear magnetic resonance* Protein nuclear magnetic resonance spectroscopy* Proton NMR* Carbon-13 NMR...
and dynamic light scattering
Dynamic light scattering
thumb|right|350px|Hypothetical Dynamic light scattering of two samples: Larger particles on the top and smaller particle on the bottomDynamic light scattering is a technique in physics that can be used to determine the size distribution profile of small particles in suspension or polymers...
).
Rotation friction factor
There are two rotational friction factors for a general spheroid, one for a rotation about the axial semiaxis (denoted ) and other for a rotation about one of the equatorial semiaxes (denoted
) and other for a rotation about one of the equatorial semiaxes (denoted 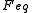 ).
).Perrin
Jean Baptiste Perrin
Jean Baptiste Perrin was a French physicist and Nobel laureate.-Early years:Born in Lille, France, Perrin attended the École Normale Supérieure, the elite grande école in Paris. He became an assistant at the school during the period of 1894-97 when he began the study of cathode rays and X-rays...
showed that
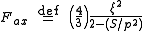
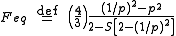
for both prolate and oblate spheroids. For spheres,
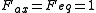 , as may be seen by taking the limit
, as may be seen by taking the limit 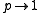 .
.These formulae may be numerically unstable when
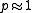 , since the numerator and denominator both go to zero into the
, since the numerator and denominator both go to zero into the 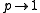 limit. In such cases, it may be better to expand in a series, e.g.,
limit. In such cases, it may be better to expand in a series, e.g.,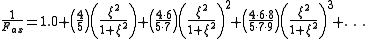
for oblate spheroids.
Time constants for rotational relaxation
The rotational friction factors are rarely observed directly. Rather, one measures the exponential rotational relaxation(s) in response to an orienting force (such as flow, applied electric field, etc.). The time constant for relaxation of the axial direction vector is
whereas that for the equatorial direction vectors is
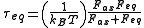
These time constants can differ significantly when the axial ratio
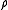 deviates significantly from 1, especially for prolate spheroids. Experimental methods for measuring these time constants include fluorescence anisotropy
deviates significantly from 1, especially for prolate spheroids. Experimental methods for measuring these time constants include fluorescence anisotropyFluorescence anisotropy
Fluorescence anisotropy is the phenomenon where the light emitted by a fluorophore has unequal intensities along different axes of polarization...
, NMR
NMR
NMR may refer to:Applications of Nuclear Magnetic Resonance:* Nuclear magnetic resonance* NMR spectroscopy* Solid-state nuclear magnetic resonance* Protein nuclear magnetic resonance spectroscopy* Proton NMR* Carbon-13 NMR...
, flow birefringence
Flow birefringence
In biochemistry, flow birefringence is a hydrodynamic technique for measuring the rotational diffusion constants . The birefringence of a solution sandwiched between two concentric cylinders is measured as a function of the difference in rotational speed between the inner and outer cylinders...
and dielectric spectroscopy
Dielectric spectroscopy
Dielectric spectroscopy , and also known as electrochemical impedance spectroscopy, measures the dielectric properties of a medium as a function of frequency...
.
It may seem paradoxical that
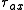 involves
involves 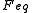 . This arises because re-orientations of the axial direction vector occur through rotations about the perpendicular axes, i.e., about the equatorial axes. Similar reasoning pertains to
. This arises because re-orientations of the axial direction vector occur through rotations about the perpendicular axes, i.e., about the equatorial axes. Similar reasoning pertains to  .
.

