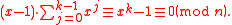Root of unity modulo n
Encyclopedia
In mathematics
, a k-th root of unity modulo n for positive integer
s k, n ≥ 2, is a solution x to the congruence
 . If k is the smallest such exponent for x, then x is called a primitive k-th root of unity modulo n.
. If k is the smallest such exponent for x, then x is called a primitive k-th root of unity modulo n.
Do not confuse this with a primitive element modulo n
, where the primitive element must generate all units
of the residue class ring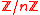 by exponentiation.
by exponentiation.
That is, there are always roots and primitive roots of unity modulo n for n ≥ 2, but for some n there is no primitive element modulo n. Being a root or a primitive root modulo n always depends on the exponent k and the modulus n, whereas being a primitive element modulo n only depends on the modulus n — the exponent is automatically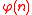 .
.
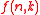 .
.
It satisfies a number of properties:
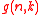 .
.
It satisfies the following properties:
you can check that .
.
If this is true, x is a k-th root of unity modulo n but not necessarily primitive.
If it is not a primitive root, then there would be some divisor ℓ of k, with .
.
In order to exclude this possibility, one has only to check for a few ℓ's equal k divided by a prime.
That is, what needs to be checked is: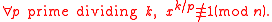
 -th roots are most frequent.
-th roots are most frequent.
It is thus recommended to try some integers for being a primitive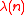 -th root, what will succeed quickly.
-th root, what will succeed quickly.
For a primitive -th root x, the number
-th root x, the number 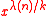 is a primitive
is a primitive  -th root of unity.
-th root of unity.
If k does not divide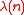 , then there will be no k-th roots of unity, at all.
, then there will be no k-th roots of unity, at all.
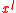 is a
is a  -th root of unity, but not necessarily a primitive one. The power
-th root of unity, but not necessarily a primitive one. The power 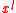 is a primitive
is a primitive  -th root of unity if and only if
-th root of unity if and only if  and
and 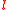 are coprime
are coprime
. The proof is as follows: If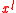 is not primitive, then there exists a divisor
is not primitive, then there exists a divisor  of
of  with
with 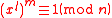 , and since
, and since  and
and 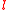 are coprime, there exists an inverse
are coprime, there exists an inverse 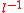 of
of 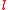 modulo
modulo  . This yields
. This yields 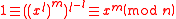 , which means that
, which means that  is not a primitive
is not a primitive  -th root of unity because there is the smaller exponent
-th root of unity because there is the smaller exponent  .
.
That is, by exponentiating x one can obtain different primitive k-th roots of unity, but these may not be all such roots. However, finding all of them is not so easy.
different primitive k-th roots of unity, but these may not be all such roots. However, finding all of them is not so easy.
You need it for instance if you want to compute a Discrete Fourier Transform
(more precisely a Number theoretic transform) of a -dimensional integer vector
-dimensional integer vector
.
In order to perform the inverse transform, you also need to divide by , that is, k shall also be a unit modulo
, that is, k shall also be a unit modulo  .
.
A simple way to find such an n is to check for primitive k-th roots with respect to the moduli in the arithmetic progression
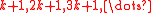 .
.
All of these moduli are coprime to k and thus k is a unit. According to Dirichlet's theorem on arithmetic progressions
there are infinitely many primes in the progression,
and for a prime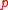 it holds
it holds 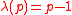 .
.
Thus if is prime then
is prime then  and thus you have primitive k-th roots of unity.
and thus you have primitive k-th roots of unity.
But the test for primes is too strong, you may find other appropriate moduli.
 such that there are primitive
such that there are primitive 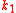 -th,
-th, 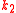 -th, ...,
-th, ...,  -th roots of unity modulo
-th roots of unity modulo  , the following theorem reduces the problem to a simpler one:
, the following theorem reduces the problem to a simpler one:
Proof
Backward direction:
If there is a primitive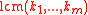 -th root of unity modulo
-th root of unity modulo  called
called  , then
, then 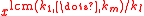 is a
is a 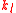 -th root of unity modulo
-th root of unity modulo  .
.
Forward direction:
If there are primitive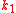 -th, ...,
-th, ..., 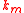 -th roots of unity modulo
-th roots of unity modulo  , then all exponents
, then all exponents 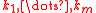 are divisors of
are divisors of 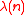 . This implies
. This implies  and this in turn means there is a primitive
and this in turn means there is a primitive 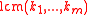 -th root of unity modulo
-th root of unity modulo  .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a k-th root of unity modulo n for positive integer
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s k, n ≥ 2, is a solution x to the congruence
Congruence
Congruence is the state achieved by coming together, the state of agreement. The Latin congruō meaning “I meet together, I agree”. As an abstract term, congruence means similarity between objects...
 . If k is the smallest such exponent for x, then x is called a primitive k-th root of unity modulo n.
. If k is the smallest such exponent for x, then x is called a primitive k-th root of unity modulo n.Do not confuse this with a primitive element modulo n
Primitive root modulo n
In modular arithmetic, a branch of number theory, a primitive root modulo n is any number g with the property that any number coprime to n is congruent to a power of g modulo n. In other words, g is a generator of the multiplicative group of integers modulo n...
, where the primitive element must generate all units
Unit (ring theory)
In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
of the residue class ring
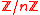 by exponentiation.
by exponentiation.That is, there are always roots and primitive roots of unity modulo n for n ≥ 2, but for some n there is no primitive element modulo n. Being a root or a primitive root modulo n always depends on the exponent k and the modulus n, whereas being a primitive element modulo n only depends on the modulus n — the exponent is automatically
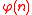 .
.Properties
- If x is a k-th root of unity, then x is a unit (invertible) whose inverse is
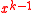 . That is, x and n are coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. That is, x and n are coprimeCoprimeIn number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. - If x is a unit, then it is a (primitive) k-th root of unity modulo n, where k is the multiplicative orderMultiplicative orderIn number theory, given an integer a and a positive integer n with gcd = 1, the multiplicative order of a modulo n is the smallest positive integer k withThe order of a modulo n is usually written ordn, or On.- Example :To determine the multiplicative order of 4 modulo 7, we compute 42 = 16 ≡ 2 ...
of x modulo n. - If x is a k-th root of unity and
 is not a zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
is not a zero divisorZero divisorIn abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
, then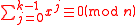 , because
, because
Number of k-th roots
For the lack of a widely accepted symbol, we denote the number of k-th roots of unity modulo n by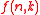 .
.It satisfies a number of properties:
-
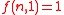 for
for 
-
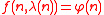 where λ denotes the Carmichael function and
where λ denotes the Carmichael function and  denotes Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
denotes Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that... -
 is a multiplicative functionMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then...
is a multiplicative functionMultiplicative functionIn number theory, a multiplicative function is an arithmetic function f of the positive integer n with the property that f = 1 and whenevera and b are coprime, then... -
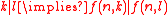 where the bar denotes divisibility
where the bar denotes divisibility -
 where
where  denotes the least common multipleLeast common multipleIn arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b...
denotes the least common multipleLeast common multipleIn arithmetic and number theory, the least common multiple of two integers a and b, usually denoted by LCM, is the smallest positive integer that is a multiple of both a and b... - For primePrimeA prime is a natural number that has exactly two distinct natural number divisors: 1 and itself.Prime or PRIME may also refer to:In mathematics:*Prime , the ′ mark, typically used as a suffix...
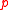 ,
, 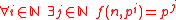 . The precise mapping from
. The precise mapping from  to
to 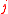 is not known. If it would be known, then together with the previous law it would yield a way to evaluate
is not known. If it would be known, then together with the previous law it would yield a way to evaluate  quickly.
quickly.
Properties
- The maximum possible radix exponent for primitive roots modulo
 is
is 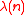 , where λ denotes the Carmichael function.
, where λ denotes the Carmichael function. - A radix exponent for a primitive root of unity is a divisorDivisorIn mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
of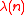 .
. - Every divisor
 of
of 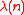 yields a primitive
yields a primitive  -th root of unity. You can obtain one by chosing a
-th root of unity. You can obtain one by chosing a 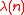 -th primitive root of unity (that must exist by definition of λ), named
-th primitive root of unity (that must exist by definition of λ), named  and compute the power
and compute the power 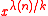 .
. - If x is a primitive k-th root of unity and also a (not necessarily primitive) ℓ-th root of unity, then k is a divisor of ℓ. This is true, because Bézout's identityBézout's identityIn number theory, Bézout's identity for two integers a, b is an expressionwhere x and y are integers , such that d is a common divisor of a and b. Bézout's lemma states that such coefficients exist for every pair of nonzero integers...
yields an integer linear combinationLinear combinationIn mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of k and ℓ equal to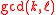 . Since k is minimal, it must be
. Since k is minimal, it must be  and
and  is a divisor of ℓ.
is a divisor of ℓ.
Number of primitive k-th roots
For the lack of a widely accepted symbol, we denote the number of primitive k-th roots of unity modulo n by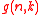 .
.It satisfies the following properties:
-
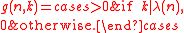
- Consequently the function
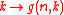 has
has 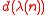 values different from zero, where
values different from zero, where  computes the number of divisors.
computes the number of divisors. -
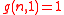
-
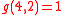
-
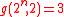 for
for  , since -1 is always a square rootSquare rootIn mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
, since -1 is always a square rootSquare rootIn mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of 1. -
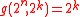 for
for 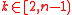
-
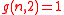 for
for  and
and  in
in -
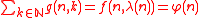 with
with  being Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that...
being Euler's totient functionEuler's totient functionIn number theory, the totient \varphi of a positive integer n is defined to be the number of positive integers less than or equal to n that are coprime to n In number theory, the totient \varphi(n) of a positive integer n is defined to be the number of positive integers less than or equal to n that... - The connection between
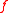 and
and 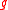 can be written in an elegant way using a Dirichlet convolutionDirichlet convolutionIn mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
can be written in an elegant way using a Dirichlet convolutionDirichlet convolutionIn mathematics, the Dirichlet convolution is a binary operation defined for arithmetic functions; it is important in number theory. It was developed by Johann Peter Gustav Lejeune Dirichlet, a German mathematician.-Definition:...
:
-
-
 , i.e.
, i.e. 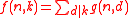
-
- You can compute values of
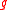 recursively from
recursively from 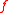 using this formula, which is equivalent to the Möbius inversion formulaMöbius inversion formulaIn mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
using this formula, which is equivalent to the Möbius inversion formulaMöbius inversion formulaIn mathematics, the classic Möbius inversion formula was introduced into number theory during the 19th century by August Ferdinand Möbius. Other Möbius inversion formulas are obtained when different local finite partially ordered sets replace the classic case of the natural numbers ordered by...
.
Testing whether x is a primitive k-th root of unity modulo n
By fast exponentiationExponentiation by squaring
Exponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
you can check that
 .
.If this is true, x is a k-th root of unity modulo n but not necessarily primitive.
If it is not a primitive root, then there would be some divisor ℓ of k, with
 .
.In order to exclude this possibility, one has only to check for a few ℓ's equal k divided by a prime.
That is, what needs to be checked is:
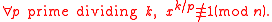
Finding a primitive k-th root of unity modulo n
Among the primitive k-th roots of unity, the primitive -th roots are most frequent.
-th roots are most frequent.It is thus recommended to try some integers for being a primitive
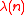 -th root, what will succeed quickly.
-th root, what will succeed quickly.For a primitive
 -th root x, the number
-th root x, the number 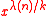 is a primitive
is a primitive  -th root of unity.
-th root of unity.If k does not divide
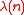 , then there will be no k-th roots of unity, at all.
, then there will be no k-th roots of unity, at all.Finding multiple primitive k-th roots modulo n
Once you have a primitive k-th root of unity x, every power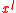 is a
is a  -th root of unity, but not necessarily a primitive one. The power
-th root of unity, but not necessarily a primitive one. The power 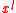 is a primitive
is a primitive  -th root of unity if and only if
-th root of unity if and only if  and
and 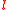 are coprime
are coprimeCoprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
. The proof is as follows: If
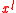 is not primitive, then there exists a divisor
is not primitive, then there exists a divisor  of
of  with
with 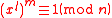 , and since
, and since  and
and 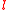 are coprime, there exists an inverse
are coprime, there exists an inverse 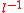 of
of 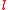 modulo
modulo  . This yields
. This yields 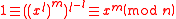 , which means that
, which means that  is not a primitive
is not a primitive  -th root of unity because there is the smaller exponent
-th root of unity because there is the smaller exponent  .
.That is, by exponentiating x one can obtain
 different primitive k-th roots of unity, but these may not be all such roots. However, finding all of them is not so easy.
different primitive k-th roots of unity, but these may not be all such roots. However, finding all of them is not so easy.Finding an n with a primitive k-th root of unity modulo n
You may want to know, in what integer residue class rings you have a primitive k-th root of unity.You need it for instance if you want to compute a Discrete Fourier Transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(more precisely a Number theoretic transform) of a
 -dimensional integer vector
-dimensional integer vectorVector (mathematics and physics)
In mathematics and physics, a vector is an element of a vector space. If n is a non negative integer and K is either the field of the real numbers or the field of the complex number, then K^n is naturally endowed with a structure of vector space, where K^n is the set of the ordered sequences of n...
.
In order to perform the inverse transform, you also need to divide by
 , that is, k shall also be a unit modulo
, that is, k shall also be a unit modulo  .
.A simple way to find such an n is to check for primitive k-th roots with respect to the moduli in the arithmetic progression
Arithmetic progression
In mathematics, an arithmetic progression or arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant...
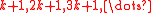 .
.All of these moduli are coprime to k and thus k is a unit. According to Dirichlet's theorem on arithmetic progressions
Dirichlet's theorem on arithmetic progressions
In number theory, Dirichlet's theorem, also called the Dirichlet prime number theorem, states that for any two positive coprime integers a and d, there are infinitely many primes of the form a + nd, where n ≥ 0. In other words, there are infinitely many primes which are...
there are infinitely many primes in the progression,
and for a prime
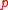 it holds
it holds 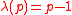 .
.Thus if
 is prime then
is prime then  and thus you have primitive k-th roots of unity.
and thus you have primitive k-th roots of unity.But the test for primes is too strong, you may find other appropriate moduli.
Finding an n with multiple primitive roots of unity modulo n
If you want to have a modulus such that there are primitive
such that there are primitive 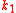 -th,
-th, 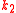 -th, ...,
-th, ...,  -th roots of unity modulo
-th roots of unity modulo  , the following theorem reduces the problem to a simpler one:
, the following theorem reduces the problem to a simpler one:- For given
 there are primitive
there are primitive 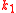 -th, ...,
-th, ...,  -th roots of unity modulo
-th roots of unity modulo  if and only if there is a primitive
if and only if there is a primitive 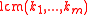 -th root of unity modulo n.
-th root of unity modulo n.
Proof
Backward direction:
If there is a primitive
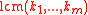 -th root of unity modulo
-th root of unity modulo  called
called  , then
, then 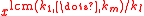 is a
is a 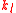 -th root of unity modulo
-th root of unity modulo  .
.Forward direction:
If there are primitive
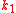 -th, ...,
-th, ..., 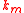 -th roots of unity modulo
-th roots of unity modulo  , then all exponents
, then all exponents 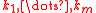 are divisors of
are divisors of 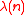 . This implies
. This implies  and this in turn means there is a primitive
and this in turn means there is a primitive 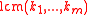 -th root of unity modulo
-th root of unity modulo  .
.