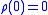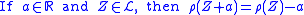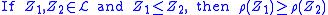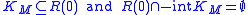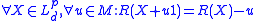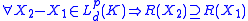Risk measure
Encyclopedia
A Risk measure is used to determine the amount of an asset
or set of assets (traditionally currency
) to be kept in reserve. The purpose of this reserve is to make the risks
taken by financial institutions, such as banks and insurance companies, acceptable to the regulator
. In recent years attention has turned towards convex and coherent risk measurement
.
 is
is 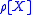 . A risk measure
. A risk measure 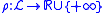 should have certain properties:
should have certain properties:
Normalized
Translative
Monotone
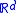 -valued portfolios such that risk can be measured in
-valued portfolios such that risk can be measured in  of the assets, then a set of portfolios is the proper way to depict risk. Set-valued risk measures are useful for markets with transaction cost
of the assets, then a set of portfolios is the proper way to depict risk. Set-valued risk measures are useful for markets with transaction cost
s.
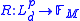 , where
, where 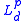 is a
is a  -dimensional Lp space
-dimensional Lp space
, , and
, and 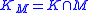 where
where  is a constant solvency cone
is a constant solvency cone
and is the set of portfolios of the
is the set of portfolios of the  reference assets.
reference assets.  must have the following properties:
must have the following properties:
Normalized
Translative in M
Monotone
(or standard deviation
) is not a risk measure. This can be seen since it has neither the translation property or monotonicity. That is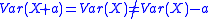 for all
for all  , and a simple counterexample for monotonicity can be found. The standard deviation is a deviation risk measure
, and a simple counterexample for monotonicity can be found. The standard deviation is a deviation risk measure
.
and a corresponding risk measure. As defined below it can be shown that and
and 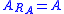 .
.
D and an expectation-bounded risk measure where for any
where for any 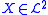
 is expectation bounded if
is expectation bounded if 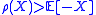 for any nonconstant X and
for any nonconstant X and  for any constant X.
for any constant X.
Asset
In financial accounting, assets are economic resources. Anything tangible or intangible that is capable of being owned or controlled to produce value and that is held to have positive economic value is considered an asset...
or set of assets (traditionally currency
Currency
In economics, currency refers to a generally accepted medium of exchange. These are usually the coins and banknotes of a particular government, which comprise the physical aspects of a nation's money supply...
) to be kept in reserve. The purpose of this reserve is to make the risks
Downside risk
Downside risk is the financial risk associated with losses. That is, the risk of difference between the actual return and the expected return , or the uncertainty of that return....
taken by financial institutions, such as banks and insurance companies, acceptable to the regulator
Regulator (economics)
Economic regulators are usually the agencies established by central government for the control of or intervention in the operation of markets, according to public interest principles and criteria....
. In recent years attention has turned towards convex and coherent risk measurement
Coherent risk measure
In the field of financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have...
.
Mathematically
A risk measure is defined as a mapping from a set of random variables to the real numbers. This set of random variables represents the risk at hand. The common notation for a risk measure associated with a random variable is
is 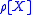 . A risk measure
. A risk measure 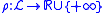 should have certain properties:
should have certain properties:Normalized
Translative
Monotone
Set-valued
In a situation with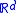 -valued portfolios such that risk can be measured in
-valued portfolios such that risk can be measured in  of the assets, then a set of portfolios is the proper way to depict risk. Set-valued risk measures are useful for markets with transaction cost
of the assets, then a set of portfolios is the proper way to depict risk. Set-valued risk measures are useful for markets with transaction costTransaction cost
In economics and related disciplines, a transaction cost is a cost incurred in making an economic exchange . For example, most people, when buying or selling a stock, must pay a commission to their broker; that commission is a transaction cost of doing the stock deal...
s.
Mathematically
A set-valued risk measure is a function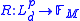 , where
, where 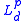 is a
is a  -dimensional Lp space
-dimensional Lp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
,
 , and
, and 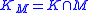 where
where  is a constant solvency cone
is a constant solvency coneSolvency cone
The solvency cone is a concept used in financial mathematics which models the possible trades in the financial market. This is of particular interest to markets with transaction costs...
and
 is the set of portfolios of the
is the set of portfolios of the  reference assets.
reference assets.  must have the following properties:
must have the following properties:Normalized
Translative in M
Monotone
Well known risk measures
- Value at riskValue at riskIn financial mathematics and financial risk management, Value at Risk is a widely used risk measure of the risk of loss on a specific portfolio of financial assets...
- Expected shortfallExpected shortfallExpected shortfall is a risk measure, a concept used in finance to evaluate the market risk or credit risk of a portfolio. It is an alternative to value at risk that is more sensitive to the shape of the loss distribution in the tail of the distribution...
- Tail conditional expectation
- Entropic risk measureEntropic risk measureIn financial mathematics, the entropic risk measure is a risk measure which depends on the risk aversion of the user through the exponential utility function. This makes it a theoretically interesting measure because it would provide different risk values for different individuals...
- Superhedging priceSuperhedging priceThe superhedging price is a coherent risk measure. The superhedging price of a portfolio is equivalent to the smallest amount necessary to be paid for a portfolio at the current time so that at some specified future time the value of B is at least as great as A...
- ...
Variance
VarianceVariance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
(or standard deviation
Standard deviation
Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
) is not a risk measure. This can be seen since it has neither the translation property or monotonicity. That is
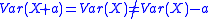 for all
for all  , and a simple counterexample for monotonicity can be found. The standard deviation is a deviation risk measure
, and a simple counterexample for monotonicity can be found. The standard deviation is a deviation risk measureDeviation risk measure
In financial mathematics, a deviation risk measure is a function to quantify financial risk in a different method than a general risk measure...
.
Relation to Acceptance Set
There is a one-to-one correspondence between an acceptance setAcceptance set
In financial mathematics, acceptance sets are a mathematical concept related to risk measures. As the name suggests an acceptance set is a set of acceptable future net worth, which are acceptable to the regulator.-Mathematical Definition:...
and a corresponding risk measure. As defined below it can be shown that
 and
and 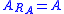 .
.Risk Measure to Acceptance Set
- If
 is a (scalar) risk measure then
is a (scalar) risk measure then 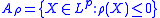 is an acceptance set.
is an acceptance set. - If
 is a set-valued risk measure then
is a set-valued risk measure then 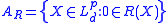 is an acceptance set.
is an acceptance set.
Acceptance Set to Risk Measure
- If
 is an acceptance set (in 1-d) then
is an acceptance set (in 1-d) then 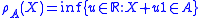 defines a (scalar) risk measure.
defines a (scalar) risk measure. - If
 is an acceptance set then
is an acceptance set then  is a set-valued risk measure.
is a set-valued risk measure.
Relation with deviation risk measure
There is a one-to-one relationship between a deviation risk measureDeviation risk measure
In financial mathematics, a deviation risk measure is a function to quantify financial risk in a different method than a general risk measure...
D and an expectation-bounded risk measure
 where for any
where for any 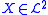
-

-
 .
.
 is expectation bounded if
is expectation bounded if 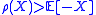 for any nonconstant X and
for any nonconstant X and  for any constant X.
for any constant X.See also
- Dynamic risk measureDynamic risk measureIn financial mathematics, a conditional risk measure is a random variable of the financial risk as if measured at some point in the future. A risk measure can be thought of as a conditional risk measure on the trivial sigma algebra.In a binomial model, the risk at any node only depends on the...
- Managerial risk accountingManagerial risk accountingManagerial Risk Accounting is concerned with the generation, dissemination and use of risk related accounting information to managers within organisations to enable them to judge and shape the risk situation of the organisation according to the objectives of the organisation.- Subject :As a part of...
- Risk managementRisk managementRisk management is the identification, assessment, and prioritization of risks followed by coordinated and economical application of resources to minimize, monitor, and control the probability and/or impact of unfortunate events or to maximize the realization of opportunities...
- RiskMetricsRiskMetricsThe RiskMetrics variance model was first established in 1989, when Sir Dennis Weatherstone, the new chairman of J.P. Morgan, asked for a daily report measuring and explaining the risks of his firm. Nearly four years later in 1992, J.P...
- Spectral risk measureSpectral risk measureA Spectral risk measure is a risk measure given as a weighted average of outcomes where bad outcomes are, typically, included with larger weights. A spectral risk measure is a function of portfolio returns and outputs the amount of the numeraire to be kept in reserve. A spectral risk measure is...