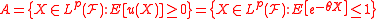Acceptance set
Encyclopedia
In financial mathematics, acceptance sets are a mathematical concept related to risk measure
s. As the name suggests an acceptance set is a set of acceptable future net worth, which are acceptable to the regulator
.
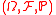 , and letting
, and letting 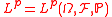 be the Lp space
be the Lp space
in the scalar case and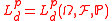 in d-dimensions, then we can define acceptance sets as below.
in d-dimensions, then we can define acceptance sets as below.
 satisfying:
satisfying:
 assets) is a set
assets) is a set 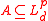 satisfying:
satisfying:
Additionally, if is convex (a convex cone
is convex (a convex cone
) then it is called a convex (coherent) acceptance set.
Note that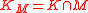 where
where  is a constant solvency cone
is a constant solvency cone
and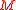 is the set of portfolios of the
is the set of portfolios of the  reference assets.
reference assets.
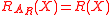 and
and  .
.
at the terminal time. That is
. That is
where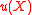 is the exponential utility
is the exponential utility
function.
Risk measure
A Risk measure is used to determine the amount of an asset or set of assets to be kept in reserve. The purpose of this reserve is to make the risks taken by financial institutions, such as banks and insurance companies, acceptable to the regulator...
s. As the name suggests an acceptance set is a set of acceptable future net worth, which are acceptable to the regulator
Financial regulation
Financial regulation is a form of regulation or supervision, which subjects financial institutions to certain requirements, restrictions and guidelines, aiming to maintain the integrity of the financial system...
.
Mathematical Definition
Given a probability space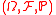 , and letting
, and letting 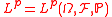 be the Lp space
be the Lp spaceLp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
in the scalar case and
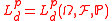 in d-dimensions, then we can define acceptance sets as below.
in d-dimensions, then we can define acceptance sets as below.Scalar Case
An acceptance set is a set satisfying:
satisfying:
-

-
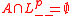 such that
such that 
-
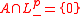
- Additionally if
 is convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
is convexConvex setIn Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
then it is a convex acceptance set- And if
 is a positively homogeneousHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
is a positively homogeneousHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
cone then it is a coherentCoherent risk measureIn the field of financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have...
acceptance set
- And if
Set-valued Case
An acceptance set (in a space with assets) is a set
assets) is a set 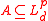 satisfying:
satisfying:
-
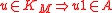 with
with 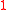 denoting the random variable that is constantly 1
denoting the random variable that is constantly 1  -a.s.
-a.s. -
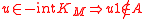
-
 is directionally closed in
is directionally closed in 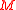 with
with 
-
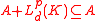
Additionally, if
 is convex (a convex cone
is convex (a convex coneConvex cone
In linear algebra, a convex cone is a subset of a vector space over an ordered field that is closed under linear combinations with positive coefficients.-Definition:...
) then it is called a convex (coherent) acceptance set.
Note that
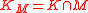 where
where  is a constant solvency cone
is a constant solvency coneSolvency cone
The solvency cone is a concept used in financial mathematics which models the possible trades in the financial market. This is of particular interest to markets with transaction costs...
and
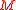 is the set of portfolios of the
is the set of portfolios of the  reference assets.
reference assets.Relation to Risk Measures
An acceptance set is convex (coherent) if and only if the corresponding risk measure is convex (coherent). As defined below it can be shown that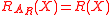 and
and  .
.Risk Measure to Acceptance Set
- If
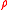 is a (scalar) risk measure then
is a (scalar) risk measure then 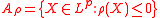 is an acceptance set.
is an acceptance set. - If
 is a set-valued risk measure then
is a set-valued risk measure then 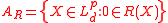 is an acceptance set.
is an acceptance set.
Acceptance Set to Risk Measure
- If
 is an acceptance set (in 1-d) then
is an acceptance set (in 1-d) then 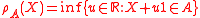 defines a (scalar) risk measure.
defines a (scalar) risk measure. - If
 is an acceptance set then
is an acceptance set then 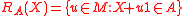 is a set-valued risk measure.
is a set-valued risk measure.
Superhedging price
The acceptance set associated with the superhedging price is the negative of the set of values of a self-financing portfolioSelf-financing portfolio
Self-financing portfolio, an important concept in financial mathematics.A portfolio is self-financing if there is no exogenous infusion or withdrawal of money; the purchase of a new asset must be financed by the sale of an old one.- Mathematical definition :...
at the terminal time. That is
-
 .
.
Entropic risk measure
The acceptance set associated with the entropic risk measure is the set of payoffs with positive expected utilityUtility
In economics, utility is a measure of customer satisfaction, referring to the total satisfaction received by a consumer from consuming a good or service....
. That is
where
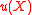 is the exponential utility
is the exponential utilityExponential utility
In economics exponential discounting is a specific form of the discount function, used in the analysis of choice over time...
function.