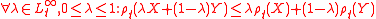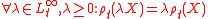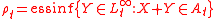Dynamic risk measure
Encyclopedia
In financial mathematics, a conditional risk measure is a random variable
of the financial risk
(particularly the downside risk
) as if measured at some point in the future. A risk measure
can be thought of as a conditional risk measure on the trivial sigma algebra.
In a binomial model, the risk at any node only depends on the possible final values branching off from that node. Therefore the conditional risk at a time in the future is the random variable on the nodes at that time. That is, when that future time is reached, the risk analyst would be able to read off the risk from the previous calculation (and inputting the current state of the market).
A dynamic risk measure is a risk measure that deals with the question of how evaluations of risk at different times are related. It can be interpreted as a sequence of conditional risk measures.
 is a conditional convex risk measure if it has the following properties:
is a conditional convex risk measure if it has the following properties:
Conditional cash invariance
Monotonicity
Conditional convexity
Normalization
If it is a conditional coherent risk measure
then it will also have the property:
Conditional positive homogeneity
at time associated with a conditional risk measure is
associated with a conditional risk measure is
If you are given an acceptance set at time then the corresponding conditional risk measure is
then the corresponding conditional risk measure is
where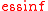 is the essential infimum.
is the essential infimum.
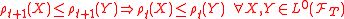 .
.
has conditional risk measures of the form: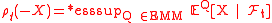 . It is a widely shown result that this is also a time consistent risk measure.
. It is a widely shown result that this is also a time consistent risk measure.
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
of the financial risk
Financial risk
Financial risk an umbrella term for multiple types of risk associated with financing, including financial transactions that include company loans in risk of default. Risk is a term often used to imply downside risk, meaning the uncertainty of a return and the potential for financial loss...
(particularly the downside risk
Downside risk
Downside risk is the financial risk associated with losses. That is, the risk of difference between the actual return and the expected return , or the uncertainty of that return....
) as if measured at some point in the future. A risk measure
Risk measure
A Risk measure is used to determine the amount of an asset or set of assets to be kept in reserve. The purpose of this reserve is to make the risks taken by financial institutions, such as banks and insurance companies, acceptable to the regulator...
can be thought of as a conditional risk measure on the trivial sigma algebra.
In a binomial model, the risk at any node only depends on the possible final values branching off from that node. Therefore the conditional risk at a time in the future is the random variable on the nodes at that time. That is, when that future time is reached, the risk analyst would be able to read off the risk from the previous calculation (and inputting the current state of the market).
A dynamic risk measure is a risk measure that deals with the question of how evaluations of risk at different times are related. It can be interpreted as a sequence of conditional risk measures.
Conditional risk measure
A conditional risk measure can be written as the worst conditional expected loss over a set of penalized probability measures. A mapping is a conditional convex risk measure if it has the following properties:
is a conditional convex risk measure if it has the following properties:Conditional cash invariance
Monotonicity
Conditional convexity
Normalization
If it is a conditional coherent risk measure
Coherent risk measure
In the field of financial economics there are a number of ways that risk can be defined; to clarify the concept theoreticians have described a number of properties that a risk measure might or might not have...
then it will also have the property:
Conditional positive homogeneity
Acceptance set
The acceptance setAcceptance set
In financial mathematics, acceptance sets are a mathematical concept related to risk measures. As the name suggests an acceptance set is a set of acceptable future net worth, which are acceptable to the regulator.-Mathematical Definition:...
at time
 associated with a conditional risk measure is
associated with a conditional risk measure is
-
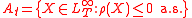 .
.
If you are given an acceptance set at time
 then the corresponding conditional risk measure is
then the corresponding conditional risk measure is
where
 is the essential infimum.
is the essential infimum.Time consistent property
A dynamic risk measure is time consistent if and only if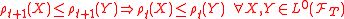 .
.Example: dynamic superhedging price
The dynamic superhedging priceSuperhedging price
The superhedging price is a coherent risk measure. The superhedging price of a portfolio is equivalent to the smallest amount necessary to be paid for a portfolio at the current time so that at some specified future time the value of B is at least as great as A...
has conditional risk measures of the form:
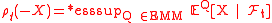 . It is a widely shown result that this is also a time consistent risk measure.
. It is a widely shown result that this is also a time consistent risk measure.