
Ricci decomposition
Encyclopedia
In semi-Riemannian geometry, the Ricci decomposition is a way of breaking up the Riemann curvature tensor of a pseudo-Riemannian manifold
into pieces with useful individual algebraic properties. This decomposition is of fundamental importance in Riemannian- and pseudo-Riemannian geometry.

The three pieces are:
Each piece possesses all the algebraic symmetries of the Riemann tensor itself, but has additional properties.
The decomposition works in slightly different ways depending on the signature of the metric tensor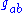 , and only makes sense if the dimension satisfies
, and only makes sense if the dimension satisfies  .
.
The scalar part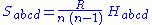
is built using the scalar curvature
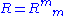 , where
, where 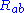 is the Ricci curvature
is the Ricci curvature
, and a tensor constructed algebraically from the metric tensor
 ,
,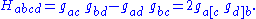
The semi-traceless part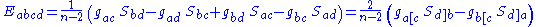
is constructed algebraically using the metric tensor and the traceless part of the Ricci tensor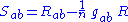
where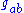 is the metric tensor
is the metric tensor
.
The Weyl tensor
or conformal curvature tensor is completely traceless, in the sense that taking the trace, or contraction
, over any pair of indices gives zero. Hermann Weyl
showed that this tensor measures the deviation of a semi-Riemannian manifold from conformal flatness; if it vanishes, the manifold is (locally) conformally equivalent
to a flat manifold.
No additional differentiation is needed anywhere in this construction.
In the case of a Lorentzian manifold, , the Einstein tensor
, the Einstein tensor
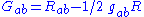 has, by design, a trace which is just the negative of the Ricci scalar, so that the traceless part of the Einstein tensor agrees with the traceless part of the Ricci tensor.
has, by design, a trace which is just the negative of the Ricci scalar, so that the traceless part of the Einstein tensor agrees with the traceless part of the Ricci tensor.
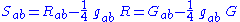
Terminological note: the notation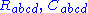 is standard in the modern literature, the notations
is standard in the modern literature, the notations 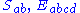 are commonly used but not standardized, and there is no standard notation for the scalar part.
are commonly used but not standardized, and there is no standard notation for the scalar part.
s having the symmetries of the Riemann tensor into its irreducible representations for the action of the orthogonal group
. Let V be an n-dimensional vector space
, equipped with a metric tensor
(of possibly mixed signature). Here V is modeled on the cotangent space
at a point, so that a curvature tensor R (with all indices lowered) is an element of the tensor product
V⊗V⊗V⊗V. The curvature tensor is skew symmetric in its first and last two entries:
and obeys the interchange symmetry
for all x,y,z,w ∈ V∗. As a result R is an element of the subspace S2Λ2V, the second symmetric power of the second exterior power of V. A curvature tensor must also satisfy the Bianchi identity, meaning that it is in the kernel
of the linear map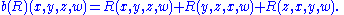
The space in S2Λ2V is the space of algebraic curvature tensors. The Ricci decomposition is the decomposition of this space into irreducible factors. The Ricci contraction mapping
is given by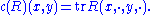
This associates a symmetric 2-form to an algebraic curvature tensor. Conversely, given a pair of symmetric 2-forms h and k, the Kulkarni–Nomizu product of h and k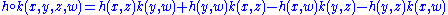
produces an algebraic curvature tensor.
If n ≥ 4, then there is an orthogonal decomposition into (unique) irreducible subspaces
where
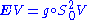 , where SV is the space of trace-free symmetric 2-forms
, where SV is the space of trace-free symmetric 2-forms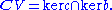
The parts S, E, and C of the Ricci decomposition of a given Riemann tensor R are the orthogonal projections of R onto these invariant factors. In particular,
is an orthogonal decomposition in the sense that
This decomposition expresses the space of tensors with Riemann symmetries as a direct sum of the scalar submodule, the Ricci submodule, and Weyl submodule, respectively. Each of these modules is an irreducible representation for the orthogonal group
, and thus the Ricci decomposition is a special case of the splitting of a module for a semisimple Lie group into its irreducible factors. In dimension 4, the Weyl module decomposes further into a pair of irreducible factors for the special orthogonal group: the self-dual and antiself-dual parts W+ and W−.
, where it is sometimes called the Géhéniau-Debever decomposition. In this theory, the Einstein field equation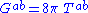
where is the stress-energy tensor
is the stress-energy tensor
describing the amount and motion of all matter and all nongravitational field energy and momentum, states that the Ricci tensor—or equivalently, the Einstein tensor—represents that part of the gravitational field which is due to the immediate presence of nongravitational energy and momentum. The Weyl tensor represents the part of the gravitational field which can propagate as a gravitational wave
through a region containing no matter or nongravitational fields. Regions of spacetime in which the Weyl tensor vanishes contain no gravitational radiation and are also conformally flat.
Pseudo-Riemannian manifold
In differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
into pieces with useful individual algebraic properties. This decomposition is of fundamental importance in Riemannian- and pseudo-Riemannian geometry.
The pieces appearing in the decomposition
The decomposition is
The three pieces are:
- the scalar part, the tensor
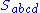
- the semi-traceless part, the tensor
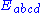
- the fully traceless part, the Weyl tensor
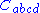
Each piece possesses all the algebraic symmetries of the Riemann tensor itself, but has additional properties.
The decomposition works in slightly different ways depending on the signature of the metric tensor
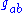 , and only makes sense if the dimension satisfies
, and only makes sense if the dimension satisfies  .
.The scalar part
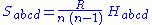
is built using the scalar curvature
Scalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
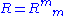 , where
, where 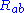 is the Ricci curvature
is the Ricci curvatureRicci curvature
In differential geometry, the Ricci curvature tensor, named after Gregorio Ricci-Curbastro, represents the amount by which the volume element of a geodesic ball in a curved Riemannian manifold deviates from that of the standard ball in Euclidean space...
, and a tensor constructed algebraically from the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
 ,
,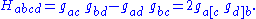
The semi-traceless part
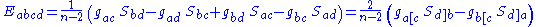
is constructed algebraically using the metric tensor and the traceless part of the Ricci tensor
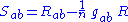
where
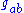 is the metric tensor
is the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
.
The Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
or conformal curvature tensor is completely traceless, in the sense that taking the trace, or contraction
Tensor contraction
In multilinear algebra, a tensor contraction is an operation on one or more tensors that arises from the natural pairing of a finite-dimensional vector space and its dual. In components, it is expressed as a sum of products of scalar components of the tensor caused by applying the summation...
, over any pair of indices gives zero. Hermann Weyl
Hermann Weyl
Hermann Klaus Hugo Weyl was a German mathematician and theoretical physicist. Although much of his working life was spent in Zürich, Switzerland and then Princeton, he is associated with the University of Göttingen tradition of mathematics, represented by David Hilbert and Hermann Minkowski.His...
showed that this tensor measures the deviation of a semi-Riemannian manifold from conformal flatness; if it vanishes, the manifold is (locally) conformally equivalent
Conformal equivalence
In mathematics and theoretical physics, two geometries are conformally equivalent if there exists a conformal transformation that maps one geometry to the other one....
to a flat manifold.
No additional differentiation is needed anywhere in this construction.
In the case of a Lorentzian manifold,
 , the Einstein tensor
, the Einstein tensorEinstein tensor
In differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
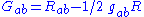 has, by design, a trace which is just the negative of the Ricci scalar, so that the traceless part of the Einstein tensor agrees with the traceless part of the Ricci tensor.
has, by design, a trace which is just the negative of the Ricci scalar, so that the traceless part of the Einstein tensor agrees with the traceless part of the Ricci tensor.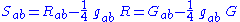
Terminological note: the notation
 is standard in the modern literature, the notations
is standard in the modern literature, the notations 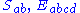 are commonly used but not standardized, and there is no standard notation for the scalar part.
are commonly used but not standardized, and there is no standard notation for the scalar part.Mathematical definition
Mathematically, the Ricci decomposition is the decomposition of the space of all tensorTensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s having the symmetries of the Riemann tensor into its irreducible representations for the action of the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
. Let V be an n-dimensional vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
, equipped with a metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
(of possibly mixed signature). Here V is modeled on the cotangent space
Cotangent space
In differential geometry, one can attach to every point x of a smooth manifold a vector space called the cotangent space at x. Typically, the cotangent space is defined as the dual space of the tangent space at x, although there are more direct definitions...
at a point, so that a curvature tensor R (with all indices lowered) is an element of the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
V⊗V⊗V⊗V. The curvature tensor is skew symmetric in its first and last two entries:

and obeys the interchange symmetry

for all x,y,z,w ∈ V∗. As a result R is an element of the subspace S2Λ2V, the second symmetric power of the second exterior power of V. A curvature tensor must also satisfy the Bianchi identity, meaning that it is in the kernel
Kernel (mathematics)
In mathematics, the word kernel has several meanings. Kernel may mean a subset associated with a mapping:* The kernel of a mapping is the set of elements that map to the zero element , as in kernel of a linear operator and kernel of a matrix...
of the linear map
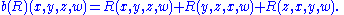
The space in S2Λ2V is the space of algebraic curvature tensors. The Ricci decomposition is the decomposition of this space into irreducible factors. The Ricci contraction mapping

is given by
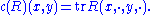
This associates a symmetric 2-form to an algebraic curvature tensor. Conversely, given a pair of symmetric 2-forms h and k, the Kulkarni–Nomizu product of h and k
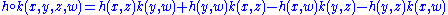
produces an algebraic curvature tensor.
If n ≥ 4, then there is an orthogonal decomposition into (unique) irreducible subspaces
where

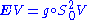 , where SV is the space of trace-free symmetric 2-forms
, where SV is the space of trace-free symmetric 2-forms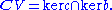
The parts S, E, and C of the Ricci decomposition of a given Riemann tensor R are the orthogonal projections of R onto these invariant factors. In particular,

is an orthogonal decomposition in the sense that

This decomposition expresses the space of tensors with Riemann symmetries as a direct sum of the scalar submodule, the Ricci submodule, and Weyl submodule, respectively. Each of these modules is an irreducible representation for the orthogonal group
Orthogonal group
In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
, and thus the Ricci decomposition is a special case of the splitting of a module for a semisimple Lie group into its irreducible factors. In dimension 4, the Weyl module decomposes further into a pair of irreducible factors for the special orthogonal group: the self-dual and antiself-dual parts W+ and W−.
Physical interpretation
The Ricci decomposition can be interpreted physically in Einstein's theory of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, where it is sometimes called the Géhéniau-Debever decomposition. In this theory, the Einstein field equation
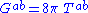
where
 is the stress-energy tensor
is the stress-energy tensorStress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
describing the amount and motion of all matter and all nongravitational field energy and momentum, states that the Ricci tensor—or equivalently, the Einstein tensor—represents that part of the gravitational field which is due to the immediate presence of nongravitational energy and momentum. The Weyl tensor represents the part of the gravitational field which can propagate as a gravitational wave
Gravitational wave
In physics, gravitational waves are theoretical ripples in the curvature of spacetime which propagates as a wave, traveling outward from the source. Predicted to exist by Albert Einstein in 1916 on the basis of his theory of general relativity, gravitational waves theoretically transport energy as...
through a region containing no matter or nongravitational fields. Regions of spacetime in which the Weyl tensor vanishes contain no gravitational radiation and are also conformally flat.
See also
- Bel decompositionBel decompositionIn semi-Riemannian geometry, the Bel decomposition, taken with respect to a specific timelike congruence, is a way of breaking up the Riemann tensor of a pseudo-Riemannian manifold into four pieces. It was introduced in 1959 by the physicist Lluis Bel....
of the Riemann tensor - Conformal geometryConformal geometryIn mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
- Schouten tensor
- Trace-free Ricci tensor

