Restriction of scalars
Encyclopedia
In abstract algebra
, restriction of scalars is a procedure of creating a module
over a ring
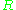from a module over another ring 
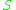, given a homomorphism
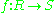between them. Intuitively speaking, the resulting module "remembers" less information than the initial one, hence the name.
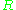and 
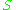be two rings (they may or may not be commutative
, or contain an identity
), and let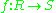
be a homomorphism. Suppose that 
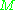is a module over 
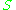. Then it can be regarded as a module over 
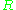, if the action of 
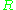is given via 
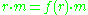for 
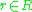and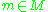 
.
from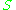
-modules to 
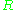-modules. An 
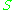-homomorphism 
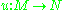automatically becomes an 
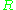-homomorphism between the restrictions of 
and 
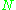. Indeed, if 
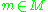and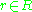 
, then
As a functor, restriction of scalars is the right adjoint of the extension of scalars
functor.
If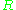
is the ring of integers, then this is just the forgetful functor from modules to abelian groups.
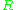and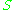 
are fields
,
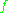is necessarily a monomorphism
, and so identifies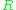
with a subfield of 
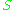. In such a case an 
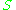-module is simply a vector space
over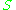
, and naturally over any subfield thereof. The module obtained by restriction is then simply a vector space over the subfield 
.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, restriction of scalars is a procedure of creating a module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
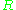from a module over another ring 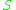, given a homomorphismRing homomorphism
In ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
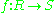between them. Intuitively speaking, the resulting module "remembers" less information than the initial one, hence the name.Definition
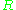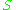Let and be two rings (they may or may not be commutativeCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
, or contain an identity
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
), and let
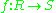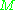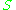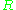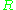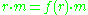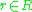be a homomorphism. Suppose that is a module over . Then it can be regarded as a module over , if the action of is given via for and 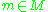.Interpretation as a functor
Restriction of scalars can be viewed as a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from
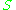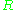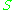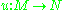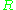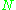-modules to -modules. An -homomorphism automatically becomes an -homomorphism between the restrictions of and . Indeed, if 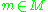and 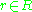, then-
.
As a functor, restriction of scalars is the right adjoint of the extension of scalars
Extension of scalars
In abstract algebra, extension of scalars is a means of producing a module over a ring S from a module over another ring R, given a homomorphism f : R \to S between them...
functor.
If
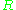is the ring of integers, then this is just the forgetful functor from modules to abelian groups.The case of fields
When both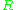 and 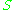are fieldsField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
,
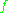is necessarily a monomorphismMonomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
, and so identifies
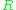with a subfield of 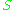. In such a case an 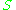-module is simply a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over
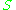, and naturally over any subfield thereof. The module obtained by restriction is then simply a vector space over the subfield .