
Regular conditional probability
Encyclopedia
Regular conditional probability is a concept that has developed to overcome certain difficulties in formally defining conditional probabilities
for continuous probability distributions. It is defined as an alternative probability measure
conditioned on a particular value of a random variable
.
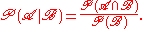
The difficulty with this arises when the event B is too small to have a non-zero probability. For example, suppose we have a random variable
X with a uniform distribution
on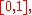 and B is the event that
and B is the event that 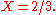 Clearly the probability of B in this case is
Clearly the probability of B in this case is 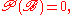 but nonetheless we would still like to assign meaning to a conditional probability such as
but nonetheless we would still like to assign meaning to a conditional probability such as 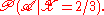 To do so rigorously requires the definition of a regular conditional probability.
To do so rigorously requires the definition of a regular conditional probability.
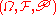 be a probability space
be a probability space
, and let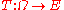 be a random variable
be a random variable
, defined as a Borel-measurable function
from to its state space
to its state space
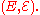 Then a regular conditional probability is defined as a function
Then a regular conditional probability is defined as a function 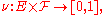 called a "transition probability", where
called a "transition probability", where 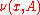 is a valid probability measure (in its second argument) on
is a valid probability measure (in its second argument) on 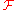 for all
for all  and a measurable function in E (in its first argument) for all
and a measurable function in E (in its first argument) for all 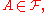 such that for all
such that for all 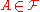 and all
and all 
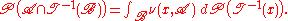
To express this in our more familiar notation: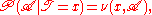
where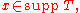 i.e. the topological support
i.e. the topological support
of the pushforward measure
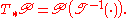 As can be seen from the integral above, the value of
As can be seen from the integral above, the value of  for points x outside the support of the random variable is meaningless; its significance as a conditional probability is strictly limited to the support of T.
for points x outside the support of the random variable is meaningless; its significance as a conditional probability is strictly limited to the support of T.
The measurable space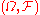 is said to have the regular conditional probability property if for all probability measure
is said to have the regular conditional probability property if for all probability measure
s on
on 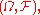 all random variable
all random variable
s on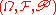 admit a regular conditional probability. A Radon space
admit a regular conditional probability. A Radon space
, in particular, has this property.
 (that is a probability measure defined on a Radon space endowed with the Borel sigma-algebra) and a real-valued random variable T. As discussed above, in this case there exists a regular conditional probability with respect to T. Moreover we can alternatively define the regular conditional probability for an event A given a particular value t of the random variable T in the following manner:
(that is a probability measure defined on a Radon space endowed with the Borel sigma-algebra) and a real-valued random variable T. As discussed above, in this case there exists a regular conditional probability with respect to T. Moreover we can alternatively define the regular conditional probability for an event A given a particular value t of the random variable T in the following manner:
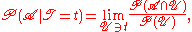
where the limit
is taken over the net
of open
neighborhoods
U of t as they become smaller with respect to set inclusion
. This limit is defined if and only if the probability space is Radon
, and only in the support of T, as described in the article. This is the restriction of the transition probability to the support of T. To describe this limiting process rigorously:
For every there exists an open neighborhood U of t, such that for every open V with
there exists an open neighborhood U of t, such that for every open V with 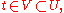
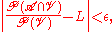
where is the limit.
is the limit.
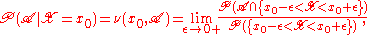
(where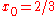 for the example given.) This limit, if it exists, is a regular conditional probability for X, restricted to
for the example given.) This limit, if it exists, is a regular conditional probability for X, restricted to 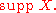
In any case, it is easy to see that this limit fails to exist for outside the support of X: since the support of a random variable is defined as the set of all points in its state space whose every neighborhood
outside the support of X: since the support of a random variable is defined as the set of all points in its state space whose every neighborhood
has positive probability, for every point outside the support of X (by definition) there will be an
outside the support of X (by definition) there will be an  such that
such that 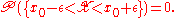
Thus if X is distributed uniformly on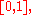 it is truly meaningless to condition a probability on "
it is truly meaningless to condition a probability on " ".
".
Note: In this article we use the Fraktur (whose shape is somewhat reminiscent of
(whose shape is somewhat reminiscent of  for Borel) to indicate a probability based on a regular measure as opposed to one based on a complete measure. The notions of regularity and completeness are incompatible
for Borel) to indicate a probability based on a regular measure as opposed to one based on a complete measure. The notions of regularity and completeness are incompatible
in a separable space.
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
for continuous probability distributions. It is defined as an alternative probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
conditioned on a particular value of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
.
Motivation
Normally we define the conditional probability of an event A given an event B as: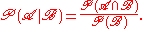
The difficulty with this arises when the event B is too small to have a non-zero probability. For example, suppose we have a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X with a uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
on
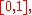 and B is the event that
and B is the event that 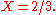 Clearly the probability of B in this case is
Clearly the probability of B in this case is 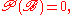 but nonetheless we would still like to assign meaning to a conditional probability such as
but nonetheless we would still like to assign meaning to a conditional probability such as 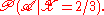 To do so rigorously requires the definition of a regular conditional probability.
To do so rigorously requires the definition of a regular conditional probability.Definition
Let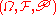 be a probability space
be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, and let
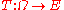 be a random variable
be a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
, defined as a Borel-measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
from
 to its state space
to its state spaceState space
In the theory of discrete dynamical systems, a state space is a directed graph where each possible state of a dynamical system is represented by a vertex, and there is a directed edge from a to b if and only if ƒ = b where the function f defines the dynamical system.State spaces are...
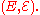 Then a regular conditional probability is defined as a function
Then a regular conditional probability is defined as a function 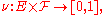 called a "transition probability", where
called a "transition probability", where 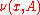 is a valid probability measure (in its second argument) on
is a valid probability measure (in its second argument) on 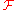 for all
for all  and a measurable function in E (in its first argument) for all
and a measurable function in E (in its first argument) for all 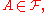 such that for all
such that for all 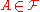 and all
and all 
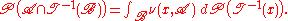
To express this in our more familiar notation:
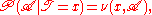
where
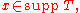 i.e. the topological support
i.e. the topological supportSupport (measure theory)
In mathematics, the support of a measure μ on a measurable topological space is a precise notion of where in the space X the measure "lives"...
of the pushforward measure
Pushforward measure
In measure theory, a pushforward measure is obtained by transferring a measure from one measurable space to another using a measurable function.-Definition:...
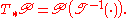 As can be seen from the integral above, the value of
As can be seen from the integral above, the value of  for points x outside the support of the random variable is meaningless; its significance as a conditional probability is strictly limited to the support of T.
for points x outside the support of the random variable is meaningless; its significance as a conditional probability is strictly limited to the support of T.The measurable space
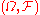 is said to have the regular conditional probability property if for all probability measure
is said to have the regular conditional probability property if for all probability measureProbability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s
 on
on 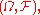 all random variable
all random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s on
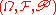 admit a regular conditional probability. A Radon space
admit a regular conditional probability. A Radon spaceRadon space
In mathematics, a Radon space, named after Johann Radon, is a separable metric space such that every Borel probability measure on M is inner regular. Since a probability measure is globally finite, and hence a locally finite measure, every probability measure on a Radon space is also a Radon...
, in particular, has this property.
Alternate definition
Consider a Radon space (that is a probability measure defined on a Radon space endowed with the Borel sigma-algebra) and a real-valued random variable T. As discussed above, in this case there exists a regular conditional probability with respect to T. Moreover we can alternatively define the regular conditional probability for an event A given a particular value t of the random variable T in the following manner:
(that is a probability measure defined on a Radon space endowed with the Borel sigma-algebra) and a real-valued random variable T. As discussed above, in this case there exists a regular conditional probability with respect to T. Moreover we can alternatively define the regular conditional probability for an event A given a particular value t of the random variable T in the following manner: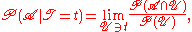
where the limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
is taken over the net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
of open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
neighborhoods
Neighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
U of t as they become smaller with respect to set inclusion
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
. This limit is defined if and only if the probability space is Radon
Radon space
In mathematics, a Radon space, named after Johann Radon, is a separable metric space such that every Borel probability measure on M is inner regular. Since a probability measure is globally finite, and hence a locally finite measure, every probability measure on a Radon space is also a Radon...
, and only in the support of T, as described in the article. This is the restriction of the transition probability to the support of T. To describe this limiting process rigorously:
For every
 there exists an open neighborhood U of t, such that for every open V with
there exists an open neighborhood U of t, such that for every open V with 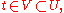
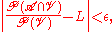
where
 is the limit.
is the limit.Example
To continue with our motivating example above, we consider a real-valued random variable X and write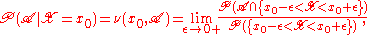
(where
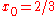 for the example given.) This limit, if it exists, is a regular conditional probability for X, restricted to
for the example given.) This limit, if it exists, is a regular conditional probability for X, restricted to 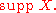
In any case, it is easy to see that this limit fails to exist for
 outside the support of X: since the support of a random variable is defined as the set of all points in its state space whose every neighborhood
outside the support of X: since the support of a random variable is defined as the set of all points in its state space whose every neighborhoodNeighbourhood (mathematics)
In topology and related areas of mathematics, a neighbourhood is one of the basic concepts in a topological space. Intuitively speaking, a neighbourhood of a point is a set containing the point where you can move that point some amount without leaving the set.This concept is closely related to the...
has positive probability, for every point
 outside the support of X (by definition) there will be an
outside the support of X (by definition) there will be an  such that
such that 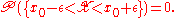
Thus if X is distributed uniformly on
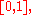 it is truly meaningless to condition a probability on "
it is truly meaningless to condition a probability on " ".
".Regularity versus completeness
| Standard probability space Standard probability space In probability theory, a standard probability space is a probability space satisfying certain assumptions introduced by Vladimir Rokhlin in 1940... |
Radon space Radon space In mathematics, a Radon space, named after Johann Radon, is a separable metric space such that every Borel probability measure on M is inner regular. Since a probability measure is globally finite, and hence a locally finite measure, every probability measure on a Radon space is also a Radon... |
|---|---|
| Lebesgue measure Lebesgue measure In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called... |
Borel measure |
| Complete measure Complete measure In mathematics, a complete measure is a measure space in which every subset of every null set is measurable... |
Regular measure Regular measure In mathematics, a regular measure on a topological space is a measure for which every measurable set is "approximately open" and "approximately closed".-Definition:... |
| Conditional probability Conditional probability In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B... |
Regular conditional probability |
| Extremely complicated and weak. | Simple and powerful. |
| Pathological Pathological (mathematics) In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved.... cases. |
No pathological cases. |
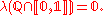 |
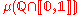 is undefined. is undefined. |
Probability is  -additive -additiveSigma additivity In mathematics, additivity and sigma additivity of a function defined on subsets of a given set are abstractions of the intuitive properties of size of a set.- Additive set functions :... |
except for sets with isolated point Isolated point In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,... s. |
Note: In this article we use the Fraktur
 (whose shape is somewhat reminiscent of
(whose shape is somewhat reminiscent of  for Borel) to indicate a probability based on a regular measure as opposed to one based on a complete measure. The notions of regularity and completeness are incompatible
for Borel) to indicate a probability based on a regular measure as opposed to one based on a complete measure. The notions of regularity and completeness are incompatibleMutually exclusive
In layman's terms, two events are mutually exclusive if they cannot occur at the same time. An example is tossing a coin once, which can result in either heads or tails, but not both....
in a separable space.
See also
- Conditioning (probability)Conditioning (probability)Beliefs depend on the available information. This idea is formalized in probability theory by conditioning. Conditional probabilities, conditional expectations and conditional distributions are treated on three levels: discrete probabilities, probability density functions, and measure theory...
- Disintegration theoremDisintegration theoremIn mathematics, the disintegration theorem is a result in measure theory and probability theory. It rigorously defines the idea of a non-trivial "restriction" of a measure to a measure zero subset of the measure space in question. It is related to the existence of conditional probability measures...
- Adherent pointAdherent pointIn mathematics, an adherent point is a slight generalization of the idea of a limit point....
- Limit pointLimit pointIn mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...

