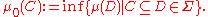Complete measure
Encyclopedia
In mathematics
, a complete measure (or, more precisely, a complete measure space) is a measure space
in which every subset
of every null set
is measurable (having measure zero). More formally, (X, Σ, μ) is complete if and only if
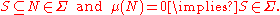
Suppose that we have already constructed Lebesgue measure
on the real line
: denote this measure space by (R, B, λ). We now wish to construct two-dimensional Lebesgue measure λ2 on the plane R2 as a product measure
. Naïvely, we would take the σ-algebra on R2 to be B ⊗ B, the smallest σ-algebra containing all measurable "rectangles" A1 × A2 for Ai ∈ B.
While this approach does define a measure space, it has a flaw. Since every singleton set has one-dimensional Lebesgue measure zero,

for "any" subset A of R. However, suppose that A is a non-measurable subset
of the real line, such as the Vitali set
. Then the λ2-measure of {0} × A is not defined, but
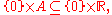
and this larger set does have λ2measure zero. So, "two-dimensional Lebesgue measure" as just defined is not complete, and some kind of completion procedure is required.
The completion can be constructed as follows:
Then (X, Σ0, μ0) is a complete measure space, and is the completion of (X, Σ, μ).
In the above construction it can be shown that every member of Σ0 is of the form A ∪ B for some A ∈ Σ and some B ∈ Z, and

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a complete measure (or, more precisely, a complete measure space) is a measure space
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
in which every subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of every null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
is measurable (having measure zero). More formally, (X, Σ, μ) is complete if and only if
Motivation
The need to consider questions of completeness can be illustrated by considering the problem of product spaces.Suppose that we have already constructed Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
: denote this measure space by (R, B, λ). We now wish to construct two-dimensional Lebesgue measure λ2 on the plane R2 as a product measure
Product measure
In mathematics, given two measurable spaces and measures on them, one can obtain the product measurable space and the product measure on that space...
. Naïvely, we would take the σ-algebra on R2 to be B ⊗ B, the smallest σ-algebra containing all measurable "rectangles" A1 × A2 for Ai ∈ B.
While this approach does define a measure space, it has a flaw. Since every singleton set has one-dimensional Lebesgue measure zero,

for "any" subset A of R. However, suppose that A is a non-measurable subset
Non-measurable set
In mathematics, a non-measurable set is a set whose structure is so complicated that it cannot be assigned any meaningful measure. Such sets are constructed to shed light on the notions of length, area and volume in formal set theory....
of the real line, such as the Vitali set
Vitali set
In mathematics, a Vitali set is an elementary example of a set of real numbers that is not Lebesgue measurable, found by . The Vitali theorem is the existence theorem that there are such sets. There are uncountably many Vitali sets, and their existence is proven on the assumption of the axiom of...
. Then the λ2-measure of {0} × A is not defined, but
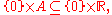
and this larger set does have λ2measure zero. So, "two-dimensional Lebesgue measure" as just defined is not complete, and some kind of completion procedure is required.
Construction of a complete measure
Given a (possibly incomplete) measure space (X, Σ, μ), there is an extension (X, Σ0, μ0) of this measure space that is complete. The smallest such extension (i.e. the smallest σ-algebra Σ0) is called the completion of the measure space.The completion can be constructed as follows:
- let Z be the set of all subsets of μ-measure zero subsets of X (intuitively, those elements of Z that are not already in Σ are the ones preventing completeness from holding true);
- let Σ0 be the σ-algebra generated by Σ and Z (i.e. the smallest σ-algebra that contains every element of Σ and of Z);
- there is a unique extension μ0 of μ to Σ0 given by the infimumInfimumIn mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
Then (X, Σ0, μ0) is a complete measure space, and is the completion of (X, Σ, μ).
In the above construction it can be shown that every member of Σ0 is of the form A ∪ B for some A ∈ Σ and some B ∈ Z, and

Examples
- Borel measure as defined on the Borel σ-algebra generated by the openOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
intervalsInterval (mathematics)In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of the real line is not complete, and so the above completion procedure must be used to define the complete Lebesgue measure. - n-dimensional Lebesgue measure is the completion of the n-fold product of the one-dimensional Lebesgue space with itself. It is also the completion of the Borel measure, as in the one-dimensional case.