Rational variety
Encyclopedia
In mathematics
, a rational variety is an algebraic variety
, over a given field
K, which is birationally equivalent to projective space
of some dimension over K. This is a question on its function field
: is it up to isomorphism
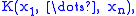
the field of all rational function
s for some set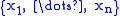
of indeterminate
s?
is rational, in the sense of being (up to isomorphism) the function field of a rational variety; such field extensions are also described as purely transcendental. More precisely, the rationality question for the field extension
is this: is 
isomorphic to a rational function field over 
in the number of indeterminates given by the transcendence degree
?
There are several different variations of this question, arising from the way in which the fields
and 
are constructed.
For example, let
be a field, and let
be indeterminates over K and let L be the field generated over K by them. Consider a finite group
permuting those indeterminates over K. By standard Galois theory
, the set of fixed points
of this group action
is a subfield of
, typically denoted 
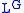. The rationality question for 
is called Noether's problem and asks if this field of fixed points is or is not a purely transcendental extension of K.
In the paper on Galois theory
she studied the problem of parameterizing the equations with given Galois group, which she reduced to "Noether's problem". (She first mentioned this problem in where she attributed the problem to E. Fischer.) She showed this was true for n = 2, 3, or 4. found a counter-example to the Noether's problem, with n = 47 and G a cyclic group of order 47.
solved in the nineteenth century, and its generalisations to higher dimensions which lie much deeper. Lüroth's problem concerns subextensions L of K(X), the rational functions in the single indeterminate X.
Any such field is either equal to K or is also rational, i.e. L = K(F) for some rational function F. In geometrical terms this states that a non-constant birational mapping from the projective line
to a curve C can only occur when C also has genus 0. That fact can be read off geometrically from the Riemann–Hurwitz formula.
and the second plurigenus. Zariski found some examples (Zariski surface
s) in characteristic p > 0 that are unirational but not rational. showed that a cubic three-fold is in general not a rational variety, providing an example for three dimensions that unirationality does not imply rationality. Their work used an intermediate Jacobian
.
showed that all non-singular quartic threefold
s are irrational, though some of them are unirational. found some unirational 3-folds with non-trivial torsion in their third cohomology group, which implies that they are not rational.
For the field of complex numbers, János Kollár
proved in 2000 that a smooth cubic hypersurface is unirational over any field K for which it has a point defined. This is an improvement of many classical results, beginning with the case of cubic surface
s (which are rational varieties over an algebraic closure). Other examples of varieties that are shown to be unirational are many cases of the moduli space
of curves
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a rational variety is an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
, over a given field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, which is birationally equivalent to projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
of some dimension over K. This is a question on its function field
Function field
Function field may refer to:*Function field of an algebraic variety*Function field...
: is it up to isomorphism
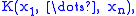
the field of all rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
s for some set
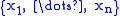of indeterminateIndeterminate
Indeterminate has a variety of meanings in mathematics:* Indeterminate * Indeterminate system* Indeterminate equation* Statically indeterminate* Indeterminate formIt is also a term in botany and gardening:*Indeterminate growth...
s?
Rationality questions
A rationality question asks whether a given field extensionField extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
is rational, in the sense of being (up to isomorphism) the function field of a rational variety; such field extensions are also described as purely transcendental. More precisely, the rationality question for the field extension
Field extension
In abstract algebra, field extensions are the main object of study in field theory. The general idea is to start with a base field and construct in some manner a larger field which contains the base field and satisfies additional properties...
is this: is isomorphic to a rational function field over in the number of indeterminates given by the transcendence degreeTranscendence degree
In abstract algebra, the transcendence degree of a field extension L /K is a certain rather coarse measure of the "size" of the extension...
?
There are several different variations of this question, arising from the way in which the fields
and are constructed.For example, let
be a field, and letbe indeterminates over K and let L be the field generated over K by them. Consider a finite group
Finite group
In mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
permuting those indeterminates over K. By standard Galois theoryGalois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
, the set of fixed points
Fixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
of this group action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
is a subfield of
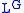, typically denoted . The rationality question for is called Noether's problem and asks if this field of fixed points is or is not a purely transcendental extension of K.In the paper on Galois theory
Galois theory
In mathematics, more specifically in abstract algebra, Galois theory, named after Évariste Galois, provides a connection between field theory and group theory...
she studied the problem of parameterizing the equations with given Galois group, which she reduced to "Noether's problem". (She first mentioned this problem in where she attributed the problem to E. Fischer.) She showed this was true for n = 2, 3, or 4. found a counter-example to the Noether's problem, with n = 47 and G a cyclic group of order 47.
Classical results
A celebrated case is Lüroth's problem, which Jacob LürothJacob Lüroth
Jacob Lüroth was a German mathematician who proved Lüroth's theorem and introduced Lüroth quartics.-References:...
solved in the nineteenth century, and its generalisations to higher dimensions which lie much deeper. Lüroth's problem concerns subextensions L of K(X), the rational functions in the single indeterminate X.
Any such field is either equal to K or is also rational, i.e. L = K(F) for some rational function F. In geometrical terms this states that a non-constant birational mapping from the projective line
Projective line
In mathematics, a projective line is a one-dimensional projective space. The projective line over a field K, denoted P1, may be defined as the set of one-dimensional subspaces of the two-dimensional vector space K2 .For the generalisation to the projective line over an associative ring, see...
to a curve C can only occur when C also has genus 0. That fact can be read off geometrically from the Riemann–Hurwitz formula.
Unirationality
A unirational variety is one covered by a rational variety, so that on the function field level it has a function field that lies in a pure transcendental field that has finite degree over it. The solution of Lüroth's problem shows that for algebraic curves, rational and unirational are the same, and Castelnuovo's theorem implies that for complex surfaces unirational implies rational, because both are characterized by the vanishing of both the arithmetic genusArithmetic genus
In mathematics, the arithmetic genus of an algebraic variety is one of some possible generalizations of the genus of an algebraic curve or Riemann surface.The arithmetic genus of a projective complex manifold...
and the second plurigenus. Zariski found some examples (Zariski surface
Zariski surface
In algebraic geometry, a branch of mathematics, a Zariski surface is a surface over a field of characteristic p > 0 such that there is a dominant inseparable map of degree p from the projective plane to the surface...
s) in characteristic p > 0 that are unirational but not rational. showed that a cubic three-fold is in general not a rational variety, providing an example for three dimensions that unirationality does not imply rationality. Their work used an intermediate Jacobian
Intermediate Jacobian
In mathematics, the intermediate Jacobian of a compact Kähler manifold or Hodge structure is a complex torus that is a common generalization of the Jacobian variety of a curve and the Picard variety and the Albanese variety. It is obtained by putting a complex structure on the torus Hn/Hn for n odd...
.
showed that all non-singular quartic threefold
Quartic threefold
In algebraic geometry, a quartic threefold is a degree 4 hypersurface of dimension 3 in 4-dimensional projective space. showed that all non-singular quartic threefolds are irrational, though some of them are unirational....
s are irrational, though some of them are unirational. found some unirational 3-folds with non-trivial torsion in their third cohomology group, which implies that they are not rational.
For the field of complex numbers, János Kollár
János Kollár
János Kollár is a Hungarian mathematician, specializing in algebraic geometry. He is a member of the National Academy of Sciences since 2005 and received the Cole Prize in 2006....
proved in 2000 that a smooth cubic hypersurface is unirational over any field K for which it has a point defined. This is an improvement of many classical results, beginning with the case of cubic surface
Cubic surface
A cubic surface is a projective variety studied in algebraic geometry. It is an algebraic surface in three-dimensional projective space defined by a single polynomial which is homogeneous of degree 3...
s (which are rational varieties over an algebraic closure). Other examples of varieties that are shown to be unirational are many cases of the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of curves
.
See also
- Rational surfaceRational surfaceIn algebraic geometry, a branch of mathematics, a rational surface is a surface birationally equivalent to the projective plane, or in other words a rational variety of dimension two...
- Severi–Brauer variety
- Birational geometryBirational geometryIn mathematics, birational geometry is a part of the subject of algebraic geometry, that deals with the geometry of an algebraic variety that is dependent only on its function field. In the case of dimension two, the birational geometry of algebraic surfaces was largely worked out by the Italian...
- Rationally connected variety