Cubic surface
Encyclopedia
A cubic surface is a projective variety studied in algebraic geometry
. It is an algebraic surface
in three-dimensional projective space
defined by a single polynomial
which is homogeneous
of degree 3 (hence, cubic). Cubic surfaces are del Pezzo surface
s.
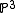has homogeneous co-ordinates 
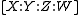, then the set of points where
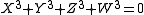
is a cubic surface called the Fermat cubic surface.
The Clebsch surface
is the set of points where
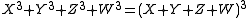
Cayley's nodal cubic surface
is the set of points where
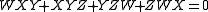
contains 27 straight lines. These can be characterized independently of the embedding into projective space as the rational lines with self-intersection number −1, or in other words the −1-curves on the surface. An Eckardt point is a point where 3 of the 27 lines meet.
A smooth cubic surface can also be described as a rational surface
obtained by blowing up
six points in the projective plane
in general position
(in this case, “general position” means no three points are aligned and no six are on a conic section). The 27 lines are the exceptional divisors above the 6 blown up points, the proper transforms of the 15 lines in
which join two of the blown up points, and the proper transforms of the 6 conics in 
which contain all but one of the blown up points.
Clebsch gave a model of a cubic surface, called the Clebsch diagonal surface, where all the 27 lines are defined over the field Q[√5], and in particular are all real.
of E6. In particular they form a basis of the 27-dimensional fundamental representation
of the group E6.
The 27 lines can be identified with the 27 possible charges of M-theory
on a six-dimensional torus
(6 momenta; 15 membranes; 6 fivebranes) and the group E6 then naturally acts as the U-duality
group. This map between del Pezzo surface
s and M-theory
on tori is known as mysterious duality.
There are other ways of thinking of these 27 lines. For example, if one projects the cubic from a point which is not on any line (most points of the cubic are like this) then we obtain a double cover of the plane branched along a smooth quartic curve. The 27 lines are mapped to 27 out of the 28 bitangents to this quartic curve; the 28th line is the image of the exceptional locus of the blow-up necessary to resolve the indeterminacy of the projection. These two objects (27 lines on the cubic, 28 bitangents on a quartic), together with the 120 tritangent planes of a canonic sextic curve of genus 4, form a "trinity" in the sense of Vladimir Arnold
, specifically a form of McKay correspondence, and can be related to many further objects, including E7 and E8, as discussed at trinities.
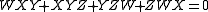
with 4 nodal singular points
at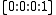
and its permutations. Singular cubic surfaces also contain rational lines, and the number and arrangement of the lines is related to the type of the singularity.
The singular cubic surfaces were classified by , and his classification was described by and
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. It is an algebraic surface
Algebraic surface
In mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
in three-dimensional projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
defined by a single polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
which is homogeneous
Homogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
of degree 3 (hence, cubic). Cubic surfaces are del Pezzo surface
Del Pezzo surface
In mathematics, a del Pezzo surface or Fano surface is a two-dimensional Fano variety, in other words a non-singular projective algebraic surface with ample anticanonical divisor class...
s.
Examples
If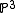 has homogeneous co-ordinates 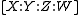, then the set of points where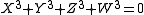is a cubic surface called the Fermat cubic surface.
The Clebsch surface
Clebsch surface
In mathematics, the Clebsch diagonal cubic surface, or Klein's icosahedral cubic surface is a cubic surface studied by and all of whose 27 exceptional linescan be defined over the real numbers...
is the set of points where
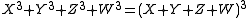
Cayley's nodal cubic surface
Cayley's nodal cubic surface
In algebraic geometry, the Cayley surface,named after Arthur Cayley, is a cubic surface in 3-dimensional projective space with four conical points. It can be given by the equation wxy+ xyz+ yzw+zwx =0\...
is the set of points where
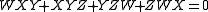
27 lines on a cubic surface
The Cayley-Salmon theorem states that a smooth cubic surface over an algebraically closed fieldAlgebraically closed field
In mathematics, a field F is said to be algebraically closed if every polynomial with one variable of degree at least 1, with coefficients in F, has a root in F.-Examples:...
contains 27 straight lines. These can be characterized independently of the embedding into projective space as the rational lines with self-intersection number −1, or in other words the −1-curves on the surface. An Eckardt point is a point where 3 of the 27 lines meet.
A smooth cubic surface can also be described as a rational surface
Rational surface
In algebraic geometry, a branch of mathematics, a rational surface is a surface birationally equivalent to the projective plane, or in other words a rational variety of dimension two...
obtained by blowing up
Blowing up
In mathematics, blowing up or blowup is a type of geometric transformation which replaces a subspace of a given space with all the directions pointing out of that subspace. For example, the blowup of a point in a plane replaces the point with the projectivized tangent space at that point...
six points in the projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
in general position
General position
In algebraic geometry, general position is a notion of genericity for a set of points, or other geometric objects. It means the general case situation, as opposed to some more special or coincidental cases that are possible...
(in this case, “general position” means no three points are aligned and no six are on a conic section). The 27 lines are the exceptional divisors above the 6 blown up points, the proper transforms of the 15 lines in
which join two of the blown up points, and the proper transforms of the 6 conics in which contain all but one of the blown up points.Clebsch gave a model of a cubic surface, called the Clebsch diagonal surface, where all the 27 lines are defined over the field Q[√5], and in particular are all real.
Related classifications
The 27 lines can also be identified with some objects arising in representation theory. In particular, these 27 lines can be identified with 27 vectors in the dual of the E6 lattice so their configuration is acted on by the Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of E6. In particular they form a basis of the 27-dimensional fundamental representation
Fundamental representation
In representation theory of Lie groups and Lie algebras, a fundamental representation is an irreducible finite-dimensional representation of a semisimple Lie group...
of the group E6.
The 27 lines can be identified with the 27 possible charges of M-theory
M-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
on a six-dimensional torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
(6 momenta; 15 membranes; 6 fivebranes) and the group E6 then naturally acts as the U-duality
U-duality
In physics, U-duality is a symmetry of string theory or M-theory combining S-duality and T-duality transformations. The term is most often met in the context of the "U-duality group" of M-theory as defined on a particular background space . This is the union of all the S- and T-dualities...
group. This map between del Pezzo surface
Del Pezzo surface
In mathematics, a del Pezzo surface or Fano surface is a two-dimensional Fano variety, in other words a non-singular projective algebraic surface with ample anticanonical divisor class...
s and M-theory
M-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
on tori is known as mysterious duality.
There are other ways of thinking of these 27 lines. For example, if one projects the cubic from a point which is not on any line (most points of the cubic are like this) then we obtain a double cover of the plane branched along a smooth quartic curve. The 27 lines are mapped to 27 out of the 28 bitangents to this quartic curve; the 28th line is the image of the exceptional locus of the blow-up necessary to resolve the indeterminacy of the projection. These two objects (27 lines on the cubic, 28 bitangents on a quartic), together with the 120 tritangent planes of a canonic sextic curve of genus 4, form a "trinity" in the sense of Vladimir Arnold
Vladimir Arnold
Vladimir Igorevich Arnold was a Soviet and Russian mathematician. While he is best known for the Kolmogorov–Arnold–Moser theorem regarding the stability of integrable Hamiltonian systems, he made important contributions in several areas including dynamical systems theory, catastrophe theory,...
, specifically a form of McKay correspondence, and can be related to many further objects, including E7 and E8, as discussed at trinities.
Singular cubic surfaces
An example of a singular cubic is Cayley's nodal cubic surfaceCayley's nodal cubic surface
In algebraic geometry, the Cayley surface,named after Arthur Cayley, is a cubic surface in 3-dimensional projective space with four conical points. It can be given by the equation wxy+ xyz+ yzw+zwx =0\...
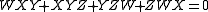
with 4 nodal singular points
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
at
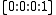and its permutations. Singular cubic surfaces also contain rational lines, and the number and arrangement of the lines is related to the type of the singularity.The singular cubic surfaces were classified by , and his classification was described by and
External links
- Lines on a Cubic Surface by Ryan Hoban (The Experimental Geometry Lab at the University of Maryland) based on work by William Goldman, The Wolfram Demonstrations Project.
- The Cubic Surfaces DVD (54 animations of cubic surfaces, downloadable separately or as a DVD)