
Penrose transform
Encyclopedia
In mathematical physics
, the Penrose transform, introduced by , is a complex analogue of the Radon transform
that relates massless fields on spacetime to cohomology
of sheaves
on complex projective space
. The projective space in question is the twistor space, a geometrical space naturally associated to the original spacetime, and the twistor transform is also geometrically natural in the sense of integral geometry
. The Penrose transform is a major component of classical twistor theory
.
of a space Y, over two spaces X and Z
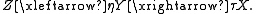
In the classical Penrose transform, Y is the spin bundle, X is a compactified and complexified form of Minkowski space
and Z is the twistor space. More generally examples come from double fibrations of the form
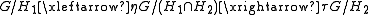
where G is a complex semisimple Lie group and H1 and H2 are parabolic subgroups.
The Penrose transform operates in two stages. First, one pulls back
the sheaf cohomology groups Hr(Z,F) to the sheaf cohomology Hr(Y,η−1F) on Y; in many cases where the Penrose transform is of interest, this pullback turns out to be an isomorphism. One then pushes the resulting cohomology classes down to X; that is, one investigates the direct image of a cohomology class by means of the Leray spectral sequence
. The resulting direct image is then interpreted in terms of differential equations. In the case of the classical
Penrose transform, the resulting differential equations are precisely the massless field equations for a given spin.
The maps from Y to X and Z are the natural projections.
used this to describe instantons in terms of algebraic vector bundles on complex projective 3-space. and explained how this could be used to classify instantions on a 4-sphere.
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, the Penrose transform, introduced by , is a complex analogue of the Radon transform
Radon transform
thumb|right|Radon transform of the [[indicator function]] of two squares shown in the image below. Lighter regions indicate larger function values. Black indicates zero.thumb|right|Original function is equal to one on the white region and zero on the dark region....
that relates massless fields on spacetime to cohomology
Sheaf cohomology
In mathematics, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian groups, that applies homological algebra to make possible effective calculation of the global sections of a sheaf F...
of sheaves
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
on complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
. The projective space in question is the twistor space, a geometrical space naturally associated to the original spacetime, and the twistor transform is also geometrically natural in the sense of integral geometry
Integral geometry
In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant transformations from the space of functions on one geometrical space to the...
. The Penrose transform is a major component of classical twistor theory
Twistor theory
In theoretical and mathematical physics, twistor theory maps the geometric objects of conventional 3+1 space-time into geometric objects in a 4 dimensional space with metric signature...
.
Overview
Abstractly, the Penrose transform operates on a double fibrationFibration
In topology, a branch of mathematics, a fibration is a generalization of the notion of a fiber bundle. A fiber bundle makes precise the idea of one topological space being "parameterized" by another topological space . A fibration is like a fiber bundle, except that the fibers need not be the same...
of a space Y, over two spaces X and Z
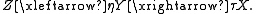
In the classical Penrose transform, Y is the spin bundle, X is a compactified and complexified form of Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
and Z is the twistor space. More generally examples come from double fibrations of the form
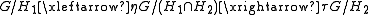
where G is a complex semisimple Lie group and H1 and H2 are parabolic subgroups.
The Penrose transform operates in two stages. First, one pulls back
Pullback
Suppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...
the sheaf cohomology groups Hr(Z,F) to the sheaf cohomology Hr(Y,η−1F) on Y; in many cases where the Penrose transform is of interest, this pullback turns out to be an isomorphism. One then pushes the resulting cohomology classes down to X; that is, one investigates the direct image of a cohomology class by means of the Leray spectral sequence
Leray spectral sequence
In mathematics, the Leray spectral sequence was a pioneering example in homological algebra, introduced in 1946 by Jean Leray. The formulation was of a spectral sequence, expressing the relationship holding in sheaf cohomology between two topological spaces X and Y, and set up by a continuous...
. The resulting direct image is then interpreted in terms of differential equations. In the case of the classical
Penrose transform, the resulting differential equations are precisely the massless field equations for a given spin.
Example
The classical example is given as follows- The "twistor space" Z is complex projective 3-space CP3, which is also the Grassmannian Gr1(C4) of lines in 4-dimensional complex space.
- X = Gr2(C4), the Grassmannian of 2-planes in 4-dimensional complex space. This is a compactification of complex Minkowski space.
- Y is the flag manifold whose elements correspond to a line in a plane of C4.
- G is the group SL4(C) and H1 and H2 are the parabolic subgroups fixing a line or a plane containing this line.
The maps from Y to X and Z are the natural projections.
Penrose–Ward transform
The Penrose–Ward transform is a non-linear modification of the Penrose transform, introduced by , that (among other things) relates holomorphic vector bundles on 3-dimensional complex projective space CP3 to solutions of the self-dual Yang–Mills equations on S4.used this to describe instantons in terms of algebraic vector bundles on complex projective 3-space. and explained how this could be used to classify instantions on a 4-sphere.

