
Funk transform
Encyclopedia
In the mathematical
field of integral geometry
, the Funk transform (also called Minkowski–Funk transform) is an integral transform defined by integrating a function
on great circle
s of the sphere
. It was introduced by Paul Funk
in 1916, based on the work of . It is closely related to the Radon transform
. The original motivation for studying the Funk transform was to describe Zoll metrics
on the sphere.
Classically, the Funk transform is defined as follows. Let ƒ be a continuous function
on the 2-sphere in R3. Then, for a unit vector x, let

where the integral is carried out with respect to the arclength ds of the great circle C(x) consisting of all unit vectors perpendicular to x:
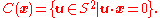
Clearly, the Funk transform annihilates all odd functions, and so it is natural to confine attention to the case when ƒ is even. In that case, the Funk transform takes even (continuous) functions to even continuous functions, and is furthermore invertible. As with the Radon transform, the inversion formula relies on the dual transform, defined by
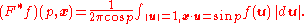
This is the average value of the circle function ƒ over circles of arc distance p from the point x. The inverse transform is given by
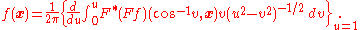
The classical formulation is invariant under the rotation group
SO(3). It is also possible to formulate the Funk transform in a manner that makes it invariant under the special linear group
SL(3,R), due to . Suppose that ƒ is a homogeneous function
of degree −2 on R3. Then, for linearly independent
vectors x and y, define a function φ by the line integral
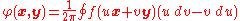
taken over a simple closed curve encircling the origin once. The differential form
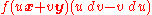
is closed
, which follows by the homogeneity of ƒ. By a change of variables
, φ satisfies

and so gives a homogeneous function of degree −1 on the exterior square
of R3,
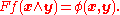
The function Fƒ : Λ2R3 → R agrees with the Funk transform when ƒ is the degree −2 homogeneous extension of a function on the sphere and the projective space associated to Λ2R3 is identified with the space of all circles on the sphere. Alternatively, Λ2R3 can be identified with R3 in an SL(3,R)-invariant manner, and so the Funk transform F maps smooth even homogeneous functions of degree −2 on R3\{0} to smooth even homogeneous functions of degree −1 on R3\{0}.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of integral geometry
Integral geometry
In mathematics, integral geometry is the theory of measures on a geometrical space invariant under the symmetry group of that space. In more recent times, the meaning has been broadened to include a view of invariant transformations from the space of functions on one geometrical space to the...
, the Funk transform (also called Minkowski–Funk transform) is an integral transform defined by integrating a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s of the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
. It was introduced by Paul Funk
Paul Funk
Paul Georg Funk was an Austrian mathematician who introduced the Funk transform and who worked on the calculus of variations. He was one of David Hilbert's students.-References:...
in 1916, based on the work of . It is closely related to the Radon transform
Radon transform
thumb|right|Radon transform of the [[indicator function]] of two squares shown in the image below. Lighter regions indicate larger function values. Black indicates zero.thumb|right|Original function is equal to one on the white region and zero on the dark region....
. The original motivation for studying the Funk transform was to describe Zoll metrics
Zoll surface
In mathematics, a Zoll surface, named after Otto Zoll, is a surface homeomorphic to the 2-sphere , equipped with a Riemannian metric all of whose geodesics are closed and of equal length. While the usual unit-sphere metric on S2 obviously has this property, it also has an infinite-dimensional...
on the sphere.
Classically, the Funk transform is defined as follows. Let ƒ be a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on the 2-sphere in R3. Then, for a unit vector x, let

where the integral is carried out with respect to the arclength ds of the great circle C(x) consisting of all unit vectors perpendicular to x:
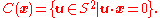
Clearly, the Funk transform annihilates all odd functions, and so it is natural to confine attention to the case when ƒ is even. In that case, the Funk transform takes even (continuous) functions to even continuous functions, and is furthermore invertible. As with the Radon transform, the inversion formula relies on the dual transform, defined by
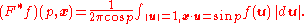
This is the average value of the circle function ƒ over circles of arc distance p from the point x. The inverse transform is given by
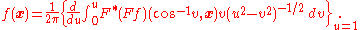
The classical formulation is invariant under the rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
SO(3). It is also possible to formulate the Funk transform in a manner that makes it invariant under the special linear group
Special linear group
In mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
SL(3,R), due to . Suppose that ƒ is a homogeneous function
Homogeneous function
In mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
of degree −2 on R3. Then, for linearly independent
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
vectors x and y, define a function φ by the line integral
Line integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
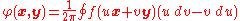
taken over a simple closed curve encircling the origin once. The differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
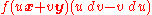
is closed
Closed and exact differential forms
In mathematics, especially vector calculus and differential topology, a closed form is a differential form α whose exterior derivative is zero , and an exact form is a differential form that is the exterior derivative of another differential form β...
, which follows by the homogeneity of ƒ. By a change of variables
Integration by substitution
In calculus, integration by substitution is a method for finding antiderivatives and integrals. Using the fundamental theorem of calculus often requires finding an antiderivative. For this and other reasons, integration by substitution is an important tool for mathematicians...
, φ satisfies

and so gives a homogeneous function of degree −1 on the exterior square
Exterior algebra
In mathematics, the exterior product or wedge product of vectors is an algebraic construction used in Euclidean geometry to study areas, volumes, and their higher-dimensional analogs...
of R3,
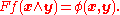
The function Fƒ : Λ2R3 → R agrees with the Funk transform when ƒ is the degree −2 homogeneous extension of a function on the sphere and the projective space associated to Λ2R3 is identified with the space of all circles on the sphere. Alternatively, Λ2R3 can be identified with R3 in an SL(3,R)-invariant manner, and so the Funk transform F maps smooth even homogeneous functions of degree −2 on R3\{0} to smooth even homogeneous functions of degree −1 on R3\{0}.

