
Quantum ergodicity
Encyclopedia
In quantum chaos
, a branch of mathematical physics
, quantum ergodicity is a property of the quantization
of classical mechanical systems
that are chaotic
in the sense of exponential sensitivity to initial conditions. Quantum ergodicity states, roughly, that in the high-energy limit, the probability distributions associated to energy eigenstates of a quantized ergodic Hamiltonian
tend to a uniform distribution
in the classical phase space
. This is consistent with the intuition that the flows of ergodic systems are equidistributed in phase space. By contrast, classical completely integrable systems generally have periodic orbits in phase space, and this is exhibited in a variety of ways in the high-energy limit of the eigenstates: typically that some form of concentration or "scarring" occurs in the limit.
The model case of a Hamiltonian is the geodesic Hamiltonian
on the cotangent bundle
of a compact
Riemannian manifold
. The quantization of the geodesic flow is given by the fundamental solution
of the Schrödinger equation
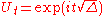
where is the square root of the Laplace-Beltrami operator
is the square root of the Laplace-Beltrami operator
. The quantum ergodicity theorem of Shnirelman, Yves Colin de Verdière
, and Zelditch states that a compact Riemannian manifold whose unit tangent bundle
is ergodic under the geodesic flow is also ergodic in the sense that the probability density associated to the nth eigenfunction of the Laplacian tends weakly to the uniform distribution on the unit cotangent bundle as n → ∞.
Quantum chaos
Quantum chaos is a branch of physics which studies how chaotic classical dynamical systems can be described in terms of quantum theory. The primary question that quantum chaos seeks to answer is, "What is the relationship between quantum mechanics and classical chaos?" The correspondence principle...
, a branch of mathematical physics
Mathematical physics
Mathematical physics refers to development of mathematical methods for application to problems in physics. The Journal of Mathematical Physics defines this area as: "the application of mathematics to problems in physics and the development of mathematical methods suitable for such applications and...
, quantum ergodicity is a property of the quantization
Quantization (physics)
In physics, quantization is the process of explaining a classical understanding of physical phenomena in terms of a newer understanding known as "quantum mechanics". It is a procedure for constructing a quantum field theory starting from a classical field theory. This is a generalization of the...
of classical mechanical systems
Classical mechanics
In physics, classical mechanics is one of the two major sub-fields of mechanics, which is concerned with the set of physical laws describing the motion of bodies under the action of a system of forces...
that are chaotic
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
in the sense of exponential sensitivity to initial conditions. Quantum ergodicity states, roughly, that in the high-energy limit, the probability distributions associated to energy eigenstates of a quantized ergodic Hamiltonian
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
tend to a uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
in the classical phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. This is consistent with the intuition that the flows of ergodic systems are equidistributed in phase space. By contrast, classical completely integrable systems generally have periodic orbits in phase space, and this is exhibited in a variety of ways in the high-energy limit of the eigenstates: typically that some form of concentration or "scarring" occurs in the limit.
The model case of a Hamiltonian is the geodesic Hamiltonian
Geodesics as Hamiltonian flows
In mathematics, the geodesic equations are second-order non-linear differential equations, and are commonly presented in the form of Euler–Lagrange equations of motion. However, they can also be presented as a set of coupled first-order equations, in the form of Hamilton's equations...
on the cotangent bundle
Cotangent bundle
In mathematics, especially differential geometry, the cotangent bundle of a smooth manifold is the vector bundle of all the cotangent spaces at every point in the manifold...
of a compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
. The quantization of the geodesic flow is given by the fundamental solution
Fundamental solution
In mathematics, a fundamental solution for a linear partial differential operator L is a formulation in the language of distribution theory of the older idea of a Green's function...
of the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
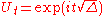
where
 is the square root of the Laplace-Beltrami operator
is the square root of the Laplace-Beltrami operatorLaplace-Beltrami operator
In differential geometry, the Laplace operator, named after Pierre-Simon Laplace, can be generalized to operate on functions defined on surfaces in Euclidean space and, more generally, on Riemannian and pseudo-Riemannian manifolds. This more general operator goes by the name Laplace–Beltrami...
. The quantum ergodicity theorem of Shnirelman, Yves Colin de Verdière
Yves Colin de Verdière
Yves Colin de Verdière is a French mathematician.He studied at the ENS in the late 1960s, obtained his PhD in 1973, and then spent the bulk of his working life in Grenoble...
, and Zelditch states that a compact Riemannian manifold whose unit tangent bundle
Unit tangent bundle
In Riemannian geometry, a branch of mathematics, the unit tangent bundle of a Riemannian manifold , denoted by UT or simply UTM, is the unit sphere bundle for the tangent bundle T...
is ergodic under the geodesic flow is also ergodic in the sense that the probability density associated to the nth eigenfunction of the Laplacian tends weakly to the uniform distribution on the unit cotangent bundle as n → ∞.

