Prüfer domain
Encyclopedia
In mathematics
, a Prüfer domain is a type of commutative ring
that generalizes Dedekind domain
s in a non-Noetherian
context. These rings possess the nice ideal
and module
theoretic properties of Dedekind domains, but usually only for finitely generated modules. Prüfer domains are named after the German
mathematician
Heinz Prüfer
.
s on the open complex plane C form a Prüfer domain. The ring of integer valued polynomials with rational number
coefficients is a Prüfer domain. While every number ring is a Dedekind domain
, their union, the ring of algebraic integers, is a Prüfer domain. Just as a Dedekind domain is locally a discrete valuation ring
, a Prüfer domain is locally a valuation ring
, so that Prüfer domains act as non-noetherian analogues of Dedekind domains. Indeed the direct limit
of Prüfer domains is a Prüfer domain, .
Many Prüfer domains are also Bézout domain
s, that is, not only are finitely generated ideals projective
, they are even free
(that is, principal
). For instance the ring of analytic functions on any noncompact Riemann surface
is a Bézout domain, , and the ring of algebraic integers is Bézout.
without zero divisor
s in which every non-zero finitely generated ideal
is invertible. Many different characterizations of Prüfer domains are known. Bourbaki lists fourteen of them, has around forty, and open with nine.
As a sample, the following conditions on an integral domain R are equivalent to R being a Prüfer domain, i.e. every finitely generated ideal of R is projective
:
Ideal arithmetic:
Localizations:
Flatness:
Integral closure:
A commutative ring is said to be arithmetical if for every maximal ideal
m in R, the localization Rm of R at m is a valuation domain. In other words, an arithmetical domain is a Prüfer domain.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Prüfer domain is a type of commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
that generalizes Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
s in a non-Noetherian
Noetherian ring
In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
context. These rings possess the nice ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
and module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
theoretic properties of Dedekind domains, but usually only for finitely generated modules. Prüfer domains are named after the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Heinz Prüfer
Heinz Prüfer
Ernst Paul Heinz Prüfer was a German mathematician, who worked on abelian groups, algebraic numbers, knot theory and Sturm-Liouville theory. His advisor was Issai Schur.- See also :* Prüfer manifold...
.
Examples
The ring of entire functionEntire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
s on the open complex plane C form a Prüfer domain. The ring of integer valued polynomials with rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
coefficients is a Prüfer domain. While every number ring is a Dedekind domain
Dedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
, their union, the ring of algebraic integers, is a Prüfer domain. Just as a Dedekind domain is locally a discrete valuation ring
Discrete valuation ring
In abstract algebra, a discrete valuation ring is a principal ideal domain with exactly one non-zero maximal ideal.This means a DVR is an integral domain R which satisfies any one of the following equivalent conditions:...
, a Prüfer domain is locally a valuation ring
Valuation ring
In abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
, so that Prüfer domains act as non-noetherian analogues of Dedekind domains. Indeed the direct limit
Direct limit
In mathematics, a direct limit is a colimit of a "directed family of objects". We will first give the definition for algebraic structures like groups and modules, and then the general definition which can be used in any category.- Algebraic objects :In this section objects are understood to be...
of Prüfer domains is a Prüfer domain, .
Many Prüfer domains are also Bézout domain
Bézout domain
In mathematics, a Bézout domain is an integral domain in which the sum of two principal ideals is again a principal ideal. This means that for every pair of elements a Bézout identity holds, and that every finitely generated ideal is principal...
s, that is, not only are finitely generated ideals projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
, they are even free
Free module
In mathematics, a free module is a free object in a category of modules. Given a set S, a free module on S is a free module with basis S.Every vector space is free, and the free vector space on a set is a special case of a free module on a set.-Definition:...
(that is, principal
Principal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
). For instance the ring of analytic functions on any noncompact Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
is a Bézout domain, , and the ring of algebraic integers is Bézout.
Definitions
A Prüfer domain is a semihereditary integral domain. Equivalently, a Prüfer domain may be defined as a commutative ringCommutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
without zero divisor
Zero divisor
In abstract algebra, a nonzero element a of a ring is a left zero divisor if there exists a nonzero b such that ab = 0. Similarly, a nonzero element a of a ring is a right zero divisor if there exists a nonzero c such that ca = 0. An element that is both a left and a right zero divisor is simply...
s in which every non-zero finitely generated ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
is invertible. Many different characterizations of Prüfer domains are known. Bourbaki lists fourteen of them, has around forty, and open with nine.
As a sample, the following conditions on an integral domain R are equivalent to R being a Prüfer domain, i.e. every finitely generated ideal of R is projective
Projective module
In mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
:
Ideal arithmetic:
- Every non-zero finitely generated ideal I of R is invertible: i.e.
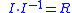, where 
and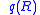 
is the field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
of R. Equivalently, every non-zero ideal generated by two elements is invertible. - For any (finitely generated) nonzero ideals I, J, K of R, the following distributivity property holds:
-
-
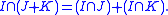
- For any (finitely generated) ideals I, J, K of R, the following distributivity property holds:
-
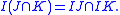
- For any (finitely generated) nonzero ideals I, J of R, the following property holds:
-
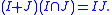
- For any finitely generated ideals I, J, K of R, if IJ = IK then J = K or I = 0.
-
Localizations:
- For every prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
P of R, the localizationLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
RP of R at P is a valuation domainValuation ringIn abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
. - For every maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
m in R, the localization Rm of R at m is a valuation domain. - R is integrally closed and every overringOverringIn mathematics, an overring B of an integral domain A is a subring of the field of fractions K of A that contains A: i.e., A \subseteq B \subseteq K....
of R (that is, a ring contained between R and its field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
) is the intersection of localizations of R
Flatness:
- Every torsion-free R-module is flatFlat moduleIn Homological algebra, and algebraic geometry, a flat module over a ring R is an R-module M such that taking the tensor product over R with M preserves exact sequences. A module is faithfully flat if taking the tensor product with a sequence produces an exact sequence if and only if the original...
. - Every torsionless R-module is flat.
- Every ideal of R is flat
- Every overring of R is R-flat
- Every submodule of a flat R-module is flat.
- If M and N are torsion-free R-modules then their tensor productTensor productIn mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
M ⊗R N is torsion-free. - If I and J are two ideals of R then I ⊗R J is torsion-free.
- The torsion submodule of every finitely generated module is a direct summand, .
Integral closure:
- Every overring of R is integrally closed
- R is integrally closed and there is some positive integer n such that for every a, b in R one has (a,b)n = (an,bn).
- R is integrally closed and each element of the quotient field K of R is a root of a polynomial in R[x] whose coefficients generate R as an R-module, .
Properties
- A commutative ring is a Dedekind domainDedekind domainIn abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
if and only if it is a Prüfer domain and NoetherianNoetherian ringIn mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
. - Though Prüfer domains need not be Noetherian, they must be coherentCoherent ringIn mathematics, a coherent ring is a ring in which every finitely generated left ideal is finitely presented.Many theorems about finitely generated modules over Noetherian rings can be extended to finitely presented modules over coherent rings....
, since finitely generated projective modules are finitely related.
- Though ideals of Dedekind domains can all be generated by two elements, for every positive integer n, there are Prüfer domains with finitely generated ideals that cannot be generated by fewer than n elements, . However, finitely generated maximal ideals of Prüfer domains are two-generated, .
- If R is a Prüfer domain, and K is its field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
, then any ring S such that R ⊆ S ⊆ K is a Prüfer domain. - If R is a Prüfer domain, K is its field of fractionsField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
, and L is an algebraic extension field of K, then the integral closure of R in L is a Prüfer domain, .
- A finitely generated module M over a Prüfer domain is projectiveProjective moduleIn mathematics, particularly in abstract algebra and homological algebra, the concept of projective module over a ring R is a more flexible generalisation of the idea of a free module...
if and only if it is torsion-free. In fact, this property characterizes Prüfer domains.
- (Gilmer–Hoffmann Theorem) Suppose that R is an integral domain, K its field of fractions, and S is the integral closure of R in K. Then S is a Prüfer domain if and only if every element of K is a root of a polynomialPolynomialIn mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
in R[X] at least one of whose coefficients is a unitUnit (ring theory)In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...
of R, .
- A commutative domain is a Dedekind domain if and only if the torsion submodule is a direct summand whenever it is bounded (M is bounded means rM = 0 for some r in R), . Similarly, a commutative domain is a Prüfer domain if and only if the torsion submodule is a direct summand whenever it is finitely generated, .
Generalizations
More generally a Prüfer ring is a commutative ring in which every non-zero finitely generated ideal consisting only of non-zero-divisors is invertible (that is, projective).A commutative ring is said to be arithmetical if for every maximal ideal
Maximal ideal
In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
m in R, the localization Rm of R at m is a valuation domain. In other words, an arithmetical domain is a Prüfer domain.