Arithmetical ring
Encyclopedia
In algebra, a commutative ring
R is said to be arithmetical (or arithmetic) if any of the following equivalent conditions holds:
The last two conditions both say that the lattice
of all ideals of R is distributive
.
An arithmetical domain
is called a Prüfer domain
.
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R is said to be arithmetical (or arithmetic) if any of the following equivalent conditions holds:
- The localizationLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
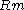of R at 
is a valuation ringValuation ringIn abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
for every maximal idealMaximal idealIn mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...
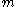of R. - For all idealsIdeal (ring theory)In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
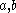, and 
,
- For all ideals
, and 
,
The last two conditions both say that the lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
of all ideals of R is distributive
Distributive lattice
In mathematics, distributive lattices are lattices for which the operations of join and meet distribute over each other. The prototypical examples of such structures are collections of sets for which the lattice operations can be given by set union and intersection...
.
An arithmetical domain
Domain (ring theory)
In mathematics, especially in the area of abstract algebra known as ring theory, a domain is a ring such that ab = 0 implies that either a = 0 or b = 0. That is, it is a ring which has no left or right zero divisors. Some authors require the ring to be nontrivial...
is called a Prüfer domain
Prüfer domain
In mathematics, a Prüfer domain is a type of commutative ring that generalizes Dedekind domains in a non-Noetherian context. These rings possess the nice ideal and module theoretic properties of Dedekind domains, but usually only for finitely generated modules...
.