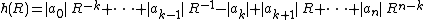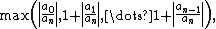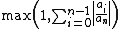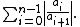Properties of polynomial roots
Encyclopedia
In mathematics
, a polynomial
is a function of the form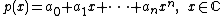
where the coefficients are
are
complex numbers and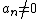 . The fundamental theorem of algebra
. The fundamental theorem of algebra
states that polynomial p has n roots. The aim of this
page is to list various properties of these roots.
on the coefficients. This means that there are n continuous functions depending on the coefficients that parametrize the roots with correct multiplicity.
depending on the coefficients that parametrize the roots with correct multiplicity.
This result implies that the eigenvalues of a matrix
depend continuously on the matrix. A proof
can be found in Tyrtyshnikov(1997).
The problem of approximating the roots given the coefficients is ill-conditioned
. See, for example, Wilkinson's polynomial.
states that if the coefficients
of a polynomial are real, then the roots appear in pairs of the type a ± ib.
For example, the equation x2 + 1 = 0 has roots ±i.
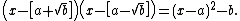
Denote this quadratic polynomial by D(x). Then, by the division transformation for polynomials,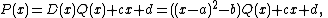
where c, d are rational numbers (by virtue of the fact that the coefficients of P(x) and D(x) are all rational). But a + √b is a root of P(x):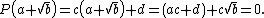
It follows that c, d must be zero, since otherwise the final equality could be arranged to suggest the irrationality of rational values (and vice versa). Hence P(x) = D(x)Q(x), for some quotient polynomial Q(x), and D(x) is a factor of P(x).
then there are exactly k (counted with multiplicity) roots of absolute value less than R. For k=0,n there is always a solution to this inequality, for example
are lower bounds for the size of all of the roots.
One can increase the separation of the roots and thus the ability to find additional separating circles from the coefficients, by applying the root squaring operation of the Dandelin-Graeffe iteration
to the polynomial.
A different approach is by using the Gershgorin circle theorem
applied to some companion matrix of the polynomial, as it is used in the Weierstraß–(Durand–Kerner) method. From initial estimates of the roots, that might be quite random, one gets unions of circles that contain the roots of the polynomial.
which is an improvement (as the geometric mean
) of
Other bounds are
or
of the roots of a polynomial contains the roots of the derivative
of the polynomial.
A sometimes useful corollary is that if all roots of a polynomial have positive real part, then so do the roots of all derivatives of the polynomial.
A related result is the Bernstein's inequality. It states that for a polynomial P of degree n with derivative P′ we have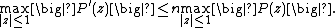
 is a polynomial such that all of its roots are real, then they are located in the interval with endpoints
is a polynomial such that all of its roots are real, then they are located in the interval with endpoints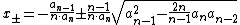 .
.
Example: The polynomial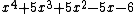 has four real roots -3, -2, -1 and 1. The formula gives
has four real roots -3, -2, -1 and 1. The formula gives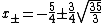 ,
,
its roots are contained in
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
is a function of the form
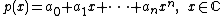
where the coefficients
 are
arecomplex numbers and
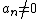 . The fundamental theorem of algebra
. The fundamental theorem of algebraFundamental theorem of algebra
The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root...
states that polynomial p has n roots. The aim of this
page is to list various properties of these roots.
Continuous dependence of coefficients
The n roots of a polynomial of degree n depend continuouslyContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on the coefficients. This means that there are n continuous functions
 depending on the coefficients that parametrize the roots with correct multiplicity.
depending on the coefficients that parametrize the roots with correct multiplicity.This result implies that the eigenvalues of a matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
depend continuously on the matrix. A proof
Mathematical proof
In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...
can be found in Tyrtyshnikov(1997).
The problem of approximating the roots given the coefficients is ill-conditioned
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
. See, for example, Wilkinson's polynomial.
Complex conjugate root theorem
The complex conjugate root theoremComplex conjugate root theorem
In mathematics, the complex conjugate root theorem states that if P is a polynomial in one variable with real coefficients, and a + bi is a root of P with a and b real numbers, then its complex conjugate a − bi is also a root of P.It follows from this , that if the degree...
states that if the coefficients
of a polynomial are real, then the roots appear in pairs of the type a ± ib.
For example, the equation x2 + 1 = 0 has roots ±i.
Radical conjugate roots
It can be proved that if a polynomial P(x) with rational coefficients has a + √b as a root, where a, b are rational and √b is irrational, then a − √b is also a root. First observe that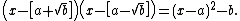
Denote this quadratic polynomial by D(x). Then, by the division transformation for polynomials,
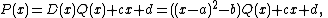
where c, d are rational numbers (by virtue of the fact that the coefficients of P(x) and D(x) are all rational). But a + √b is a root of P(x):
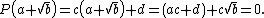
It follows that c, d must be zero, since otherwise the final equality could be arranged to suggest the irrationality of rational values (and vice versa). Hence P(x) = D(x)Q(x), for some quotient polynomial Q(x), and D(x) is a factor of P(x).
Based on the Rouché theorem
A very general class of bounds on the magnitude of roots is implied by the Rouché theorem. If there is a positive real number R and a coefficient index k such thatthen there are exactly k (counted with multiplicity) roots of absolute value less than R. For k=0,n there is always a solution to this inequality, for example
- for k=n,
-
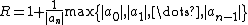 or
or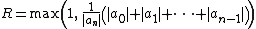
- are upper bounds for the size of all roots,
- for k=0,
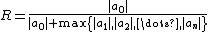 or
or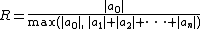
are lower bounds for the size of all of the roots.
- for all other indices, the function
-
- is convex on the positive real numbers, thus the minimizing point is easy to determine numerically. If the minimal value is negative, one has found additional information on the location of the roots.
One can increase the separation of the roots and thus the ability to find additional separating circles from the coefficients, by applying the root squaring operation of the Dandelin-Graeffe iteration
Graeffe's method
In mathematics, Graeffe's method or Dandelin–Graeffe method is an algorithm for finding all of the roots of a polynomial. It was developed independently by Germinal Pierre Dandelin in 1826 and Karl Heinrich Gräffe in 1837. Lobachevsky in 1834 also discovered the principal idea of the method....
to the polynomial.
A different approach is by using the Gershgorin circle theorem
Gershgorin circle theorem
In mathematics, the Gershgorin circle theorem may be used to bound the spectrum of a square matrix. It was first published by the Belarusian mathematician Semyon Aranovich Gershgorin in 1931. The spelling of S. A...
applied to some companion matrix of the polynomial, as it is used in the Weierstraß–(Durand–Kerner) method. From initial estimates of the roots, that might be quite random, one gets unions of circles that contain the roots of the polynomial.
Other bounds
Useful bounds for the magnitude of all polynomial's roots include the near optimal Fujiwara bound-
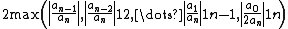 (Fujiwara's bound),
(Fujiwara's bound),
which is an improvement (as the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
) of
-
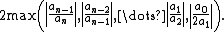 (Kojima's bound)
(Kojima's bound)
Other bounds are
or
Gauss–Lucas theorem
The Gauss–Lucas theorem states that the convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
of the roots of a polynomial contains the roots of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the polynomial.
A sometimes useful corollary is that if all roots of a polynomial have positive real part, then so do the roots of all derivatives of the polynomial.
A related result is the Bernstein's inequality. It states that for a polynomial P of degree n with derivative P′ we have
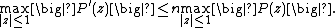
Polynomials with real roots
If is a polynomial such that all of its roots are real, then they are located in the interval with endpoints
is a polynomial such that all of its roots are real, then they are located in the interval with endpoints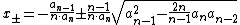 .
.Example: The polynomial
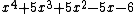 has four real roots -3, -2, -1 and 1. The formula gives
has four real roots -3, -2, -1 and 1. The formula gives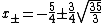 ,
,its roots are contained in
- I = [-3.8117 ; 1.3117].
See also
- Descartes' rule of signsDescartes' rule of signsIn mathematics, Descartes' rule of signs, first described by René Descartes in his work La Géométrie, is a technique for determining the number of positive or negative real roots of a polynomial....
- Sturm's theoremSturm's theoremIn mathematics, Sturm's theorem is a symbolic procedure to determine the number of distinct real roots of a polynomial. It was named for Jacques Charles François Sturm...
- Abel–Ruffini theoremAbel–Ruffini theoremIn algebra, the Abel–Ruffini theorem states that there is no general algebraic solution—that is, solution in radicals— to polynomial equations of degree five or higher.- Interpretation :...
- Viète's formulas
- Gauss–Lucas theorem
- Content (algebra)Content (algebra)In algebra, the content of a polynomial is the highest common factor of its coefficients.A polynomial is primitive if it has content unity....
- Rational root theorem
- Halley's methodHalley's methodIn numerical analysis, Halley’s method is a root-finding algorithm used for functions of one real variable with a continuous second derivative, i.e., C2 functions. It is named after its inventor Edmond Halley, who also discovered Halley's Comet....
- Laguerre's methodLaguerre's methodIn numerical analysis, Laguerre's method is a root-finding algorithm tailored to polynomials. In other words, Laguerre's method can be used to solve numerically the equation\ p = 0 for a given polynomial p...
- Jenkins-Traub method