
Principle of maximum entropy
Encyclopedia
In Bayesian probability
, the principle of maximum entropy is a postulate which states that, subject to known constraints (called testable information), the probability distribution
which best represents the current state of knowledge is the one with largest entropy.
Let some testable information about a probability distribution function be given. Consider the set of all trial probability distributions that encode this information
. Then, the probability distribution that maximizes the information entropy
is the true probability distribution with respect to the testable information prescribed.
and information theory
. In particular, Jaynes offered a new and very general rationale why the Gibbsian method of statistical mechanics works. He argued that the entropy
of statistical mechanics, and the information entropy
of information theory
, are principally the same thing. Consequently, statistical mechanics
should be seen just as a particular application of a general tool of logical inference
and information theory.
in question. This is the way the maximum entropy principle is most often used in statistical thermodynamics. Another possibility is to prescribe some symmetries of the probability distribution. An equivalence between the conserved quantities and corresponding symmetry groups implies the same level of equivalence for both these two ways of specifying the testable information in the maximum entropy method.
The maximum entropy principle is also needed to guarantee the uniqueness and consistency of probability assignments obtained by different methods, statistical mechanics
and logical inference in particular. Strictly speaking, the trial distributions, which do not maximize the entropy, are actually not probability distributions.
The maximum entropy principle makes explicit our freedom in using different forms of prior information. As a special case, a uniform prior probability
density (Laplace's principle of indifference
) may be adopted. Thus, the maximum entropy principle is not just an alternative to the methods of inference of classical statistics, but it is an important conceptual generalization of those methods.
and
are statements of testable information.
Given testable information, the maximum entropy procedure consists of seeking the probability distribution
which maximizes information entropy
, subject to the constraints of the information. This constrained optimization problem is typically solved using the method of Lagrange multipliers.
Entropy maximization with no testable information takes place under a single constraint: the sum of the probabilities must be one. Under this constraint, the maximum entropy discrete probability distribution is the uniform distribution,
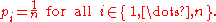
The principle of maximum entropy can thus be seen as a generalization of the classical principle of indifference
, also known as the principle of insufficient reason.
for Bayesian inference
. Jaynes was a strong advocate of this approach, claiming the maximum entropy distribution represented the least informative distribution.
A large amount of literature is now dedicated to the elicitation of maximum entropy priors and links with channel coding.
. An example of such a model is logistic regression
, which corresponds to the maximum entropy classifier for independent observations.

Furthermore, the probabilities must sum to one, giving the constraint
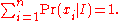
The probability distribution with maximum information entropy subject to these constraints is
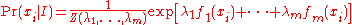
It is sometimes called the Gibbs distribution. The normalization constant is determined by

and is conventionally called the partition function
. (Interestingly, the Pitman–Koopman theorem states that the necessary and sufficient condition for a sampling distribution to admit sufficient statistics
of bounded dimension is that it have the general form of a maximum entropy distribution.)
The λk parameters are Lagrange multipliers whose particular values are determined by the constraints according to

These m simultaneous equations do not generally possess a closed form solution, and are usually solved by numerical methods
.
). Instead Edwin Jaynes (1963, 1968, 2003) gave the following formula, which is closely related to the relative entropy.
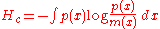
where m(x), which Jaynes called the "invariant measure", is proportional to the limiting density of discrete points
. For now, we shall assume that it is known; we will discuss it further after the solution equations are given.
A closely related quantity, the relative entropy, is usually defined as the Kullback-Leibler divergence of m from p (although it is sometimes, confusingly, defined as the negative of this). The inference principle of minimizing this, due to Kullback, is known as the Principle of Minimum Discrimination Information.
We have some testable information I about a quantity x which takes values in some interval
of the real numbers (all integrals below are over this interval). We express this information as m constraints on the expectations of the functions fk, i.e. we require our probability density function to satisfy
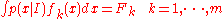
And of course, the probability density must integrate to one, giving the constraint
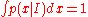
The probability density function with maximum Hc subject to these constraints is

with the partition function
determined by
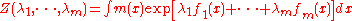
As in the discrete case, the values of the λk parameters are determined by the constraints according to

The invariant measure function m(x) can be best understood by supposing that x is known to take values only in the bounded interval (a, b), and that no other information is given. Then the maximum entropy probability density function is
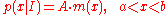
where A is a normalization constant. The invariant measure function is actually the prior density function encoding 'lack of relevant information'. It cannot be determined by the principle of maximum entropy, and must be determined by some other logical method, such as the principle of transformation groups
or marginalization theory.
s.
as given, and are thus subject to the same postulates.
s. The most informative distribution would occur when one of the propositions was known to be true. In that case, the information entropy would be equal to zero. The least informative distribution would occur when there is no reason to favor any one of the propositions over the others. In that case, the only reasonable probability distribution would be uniform, and then the information entropy would be equal to its maximum possible value,
log m. The information entropy can therefore be seen as a numerical measure which describes how uninformative a particular probability distribution is, ranging from zero (completely informative) to log m (completely uninformative).
By choosing to use the distribution with the maximum entropy allowed by our information, the argument goes, we are choosing the most uninformative distribution possible. To choose a distribution with lower entropy would be to assume information we do not possess; to choose one with a higher entropy would violate the constraints of the information we do possess. Thus the maximum entropy distribution is the only reasonable distribution.
, although the conceptual emphasis is quite different. It has the advantage of being strictly combinatorial in nature, making no reference to information entropy as a measure of 'uncertainty', 'uninformativeness', or any other imprecisely defined concept. The information entropy function is not assumed a priori, but rather is found in the course of the argument; and the argument leads naturally to the procedure of maximizing the information entropy, rather than treating it in some other way.
Suppose an individual wishes to make a probability assignment among m mutually exclusive
propositions. She has some testable information, but is not sure how to go about including this information in her probability assessment. She therefore conceives of the following random experiment. She will distribute N quanta of probability (each worth 1/N) at random among the m possibilities. (One might imagine that she will throw N balls into m buckets while blindfolded. In order to be as fair as possible, each throw is to be independent of any other, and every bucket is to be the same size.) Once the experiment is done, she will check if the probability assignment thus obtained is consistent with her information. If not, she will reject it and try again. Otherwise, her assessment will be
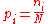
where pi is the probability of the ith proposition, while ni is the number of quanta that were assigned to the ith proposition (if the individual in our experiment carries out the ball throwing experiment, then ni is the number of balls that ended up in bucket i).
Now, in order to reduce the 'graininess' of the probability assignment, it will be necessary to use quite a large number of quanta of probability. Rather than actually carry out, and possibly have to repeat, the rather long random experiment, our protagonist decides to simply calculate and use the most probable result. The probability of any particular result is the multinomial distribution,
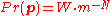
where
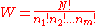
is sometimes known as the multiplicity of the outcome.
The most probable result is the one which maximizes the multiplicity W. Rather than maximizing W directly, our protagonist could equivalently maximize any monotonic increasing function of W. She decides to maximize
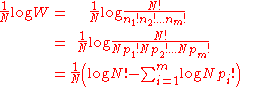
At this point, in order to simplify the expression, our protagonist takes the limit as , i.e. as the probability levels go from grainy discrete values to smooth continuous values. Using Stirling's approximation
, i.e. as the probability levels go from grainy discrete values to smooth continuous values. Using Stirling's approximation
, she finds

All that remains for our protagonist to do is to maximize entropy under the constraints of her testable information. She has found that the maximum entropy distribution is the most probable of all "fair" random distributions, in the limit as the probability levels go from discrete to continuous.
Jaynes stated Bayes' Rule was a way to calculate a probability, while Maximum Entropy was a way to assign a prior probability distribution (Jaynes 1988).
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
, the principle of maximum entropy is a postulate which states that, subject to known constraints (called testable information), the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
which best represents the current state of knowledge is the one with largest entropy.
Let some testable information about a probability distribution function be given. Consider the set of all trial probability distributions that encode this information
Information
Information in its most restricted technical sense is a message or collection of messages that consists of an ordered sequence of symbols, or it is the meaning that can be interpreted from such a message or collection of messages. Information can be recorded or transmitted. It can be recorded as...
. Then, the probability distribution that maximizes the information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
is the true probability distribution with respect to the testable information prescribed.
History
The principle was first expounded by E.T. Jaynes in two papers in 1957 where he emphasized a natural correspondence between statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
and information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
. In particular, Jaynes offered a new and very general rationale why the Gibbsian method of statistical mechanics works. He argued that the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of statistical mechanics, and the information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
of information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, are principally the same thing. Consequently, statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
should be seen just as a particular application of a general tool of logical inference
Inference
Inference is the act or process of deriving logical conclusions from premises known or assumed to be true. The conclusion drawn is also called an idiomatic. The laws of valid inference are studied in the field of logic.Human inference Inference is the act or process of deriving logical conclusions...
and information theory.
Overview
In most practical cases, the testable information is given by a set of conserved quantities (average values of some moment functions), associated with the probability distributionProbability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
in question. This is the way the maximum entropy principle is most often used in statistical thermodynamics. Another possibility is to prescribe some symmetries of the probability distribution. An equivalence between the conserved quantities and corresponding symmetry groups implies the same level of equivalence for both these two ways of specifying the testable information in the maximum entropy method.
The maximum entropy principle is also needed to guarantee the uniqueness and consistency of probability assignments obtained by different methods, statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
and logical inference in particular. Strictly speaking, the trial distributions, which do not maximize the entropy, are actually not probability distributions.
The maximum entropy principle makes explicit our freedom in using different forms of prior information. As a special case, a uniform prior probability
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
density (Laplace's principle of indifference
Principle of indifference
The principle of indifference is a rule for assigning epistemic probabilities.Suppose that there are n > 1 mutually exclusive and collectively exhaustive possibilities....
) may be adopted. Thus, the maximum entropy principle is not just an alternative to the methods of inference of classical statistics, but it is an important conceptual generalization of those methods.
Testable information
The principle of maximum entropy is useful explicitly only when applied to testable information. A piece of information is testable if it can be determined whether a given distribution is consistent with it. For example, the statements- The expectationExpected valueIn probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of the variable x is 2.87
and
- p2 + p3 > 0.6
are statements of testable information.
Given testable information, the maximum entropy procedure consists of seeking the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
which maximizes information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
, subject to the constraints of the information. This constrained optimization problem is typically solved using the method of Lagrange multipliers.
Entropy maximization with no testable information takes place under a single constraint: the sum of the probabilities must be one. Under this constraint, the maximum entropy discrete probability distribution is the uniform distribution,
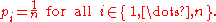
The principle of maximum entropy can thus be seen as a generalization of the classical principle of indifference
Principle of indifference
The principle of indifference is a rule for assigning epistemic probabilities.Suppose that there are n > 1 mutually exclusive and collectively exhaustive possibilities....
, also known as the principle of insufficient reason.
Applications
The principle of maximum entropy is commonly applied in two ways to inferential problems:Prior probabilities
The principle of maximum entropy is often used to obtain prior probability distributionsPrior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
for Bayesian inference
Bayesian inference
In statistics, Bayesian inference is a method of statistical inference. It is often used in science and engineering to determine model parameters, make predictions about unknown variables, and to perform model selection...
. Jaynes was a strong advocate of this approach, claiming the maximum entropy distribution represented the least informative distribution.
A large amount of literature is now dedicated to the elicitation of maximum entropy priors and links with channel coding.
Maximum entropy models
Alternatively, the principle is often invoked for model specification: in this case the observed data itself is assumed to be the testable information. Such models are widely used in natural language processingNatural language processing
Natural language processing is a field of computer science and linguistics concerned with the interactions between computers and human languages; it began as a branch of artificial intelligence....
. An example of such a model is logistic regression
Logistic regression
In statistics, logistic regression is used for prediction of the probability of occurrence of an event by fitting data to a logit function logistic curve. It is a generalized linear model used for binomial regression...
, which corresponds to the maximum entropy classifier for independent observations.
General solution for the maximum entropy distribution with linear constraints
Discrete case
We have some testable information I about a quantity x taking values in {x1, x2,..., xn}. We express this information as m constraints on the expectations of the functions fk; that is, we require our probability distribution to satisfy
Furthermore, the probabilities must sum to one, giving the constraint
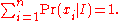
The probability distribution with maximum information entropy subject to these constraints is
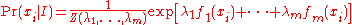
It is sometimes called the Gibbs distribution. The normalization constant is determined by

and is conventionally called the partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
. (Interestingly, the Pitman–Koopman theorem states that the necessary and sufficient condition for a sampling distribution to admit sufficient statistics
Sufficiency (statistics)
In statistics, a sufficient statistic is a statistic which has the property of sufficiency with respect to a statistical model and its associated unknown parameter, meaning that "no other statistic which can be calculated from the same sample provides any additional information as to the value of...
of bounded dimension is that it have the general form of a maximum entropy distribution.)
The λk parameters are Lagrange multipliers whose particular values are determined by the constraints according to

These m simultaneous equations do not generally possess a closed form solution, and are usually solved by numerical methods
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
.
Continuous case
For continuous distributions, the simple definition of Shannon entropy ceases to be so useful (see differential entropyDifferential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
). Instead Edwin Jaynes (1963, 1968, 2003) gave the following formula, which is closely related to the relative entropy.
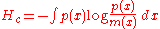
where m(x), which Jaynes called the "invariant measure", is proportional to the limiting density of discrete points
Limiting density of discrete points
In information theory, the limiting density of discrete points is an adjustment to the formula of Claude Elwood Shannon for differential entropy.It was formulated by Edwin Thompson Jaynes to address defects in the initial definition of differential entropy....
. For now, we shall assume that it is known; we will discuss it further after the solution equations are given.
A closely related quantity, the relative entropy, is usually defined as the Kullback-Leibler divergence of m from p (although it is sometimes, confusingly, defined as the negative of this). The inference principle of minimizing this, due to Kullback, is known as the Principle of Minimum Discrimination Information.
We have some testable information I about a quantity x which takes values in some interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of the real numbers (all integrals below are over this interval). We express this information as m constraints on the expectations of the functions fk, i.e. we require our probability density function to satisfy
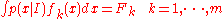
And of course, the probability density must integrate to one, giving the constraint
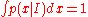
The probability density function with maximum Hc subject to these constraints is

with the partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
determined by
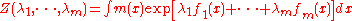
As in the discrete case, the values of the λk parameters are determined by the constraints according to

The invariant measure function m(x) can be best understood by supposing that x is known to take values only in the bounded interval (a, b), and that no other information is given. Then the maximum entropy probability density function is
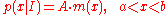
where A is a normalization constant. The invariant measure function is actually the prior density function encoding 'lack of relevant information'. It cannot be determined by the principle of maximum entropy, and must be determined by some other logical method, such as the principle of transformation groups
Principle of transformation groups
The principle of transformation groups is a rule for assigning epistemic probabilities in a statistical inference problem. It was first suggested by Edwin T Jaynes and can be seen as a generalisation of the principle of indifference....
or marginalization theory.
Examples
For several examples of maximum entropy distributions, see the article on maximum entropy probability distributionMaximum entropy probability distribution
In statistics and information theory, a maximum entropy probability distribution is a probability distribution whose entropy is at least as great as that of all other members of a specified class of distributions....
s.
Justifications for the principle of maximum entropy
Proponents of the principle of maximum entropy justify its use in assigning probabilities in several ways, including the following two arguments. These arguments take the use of Bayesian probabilityBayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
as given, and are thus subject to the same postulates.
Information entropy as a measure of 'uninformativeness'
Consider a discrete probability distribution among m mutually exclusive propositionProposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s. The most informative distribution would occur when one of the propositions was known to be true. In that case, the information entropy would be equal to zero. The least informative distribution would occur when there is no reason to favor any one of the propositions over the others. In that case, the only reasonable probability distribution would be uniform, and then the information entropy would be equal to its maximum possible value,
log m. The information entropy can therefore be seen as a numerical measure which describes how uninformative a particular probability distribution is, ranging from zero (completely informative) to log m (completely uninformative).
By choosing to use the distribution with the maximum entropy allowed by our information, the argument goes, we are choosing the most uninformative distribution possible. To choose a distribution with lower entropy would be to assume information we do not possess; to choose one with a higher entropy would violate the constraints of the information we do possess. Thus the maximum entropy distribution is the only reasonable distribution.
The Wallis derivation
The following argument is the result of a suggestion made by Graham Wallis to E. T. Jaynes in 1962 (Jaynes, 2003). It is essentially the same mathematical argument used for the Maxwell-Boltzmann statistics in statistical mechanicsStatistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, although the conceptual emphasis is quite different. It has the advantage of being strictly combinatorial in nature, making no reference to information entropy as a measure of 'uncertainty', 'uninformativeness', or any other imprecisely defined concept. The information entropy function is not assumed a priori, but rather is found in the course of the argument; and the argument leads naturally to the procedure of maximizing the information entropy, rather than treating it in some other way.
Suppose an individual wishes to make a probability assignment among m mutually exclusive
Mutually exclusive
In layman's terms, two events are mutually exclusive if they cannot occur at the same time. An example is tossing a coin once, which can result in either heads or tails, but not both....
propositions. She has some testable information, but is not sure how to go about including this information in her probability assessment. She therefore conceives of the following random experiment. She will distribute N quanta of probability (each worth 1/N) at random among the m possibilities. (One might imagine that she will throw N balls into m buckets while blindfolded. In order to be as fair as possible, each throw is to be independent of any other, and every bucket is to be the same size.) Once the experiment is done, she will check if the probability assignment thus obtained is consistent with her information. If not, she will reject it and try again. Otherwise, her assessment will be
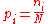
where pi is the probability of the ith proposition, while ni is the number of quanta that were assigned to the ith proposition (if the individual in our experiment carries out the ball throwing experiment, then ni is the number of balls that ended up in bucket i).
Now, in order to reduce the 'graininess' of the probability assignment, it will be necessary to use quite a large number of quanta of probability. Rather than actually carry out, and possibly have to repeat, the rather long random experiment, our protagonist decides to simply calculate and use the most probable result. The probability of any particular result is the multinomial distribution,
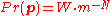
where
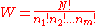
is sometimes known as the multiplicity of the outcome.
The most probable result is the one which maximizes the multiplicity W. Rather than maximizing W directly, our protagonist could equivalently maximize any monotonic increasing function of W. She decides to maximize
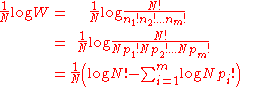
At this point, in order to simplify the expression, our protagonist takes the limit as
 , i.e. as the probability levels go from grainy discrete values to smooth continuous values. Using Stirling's approximation
, i.e. as the probability levels go from grainy discrete values to smooth continuous values. Using Stirling's approximationStirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
, she finds

All that remains for our protagonist to do is to maximize entropy under the constraints of her testable information. She has found that the maximum entropy distribution is the most probable of all "fair" random distributions, in the limit as the probability levels go from discrete to continuous.
Compatibility with Bayes Rule
Giffin et al. (2007) state that Bayes' Rule and the Principle of Maximum Entropy (MaxEnt) are completely compatible and can be seen as special cases of the Method of Maximum (relative) Entropy. They state that this method reproduces every aspect of orthodox Bayesian inference methods. In addition this new method opens the door to tackling problems that could not be addressed by either the MaxEnt or orthodox Bayesian methods individually. Moreover, recent contributions (Lazar 2003, and Schennach 2005) show that frequentist relative-entropy-based inference approaches (such as Empirical Likelihood and Exponentially Tilted Empirical Likelihood - see e.g. Owen 2001 and Kitamura 2006) can be combined with prior information to perform Bayesian posterior analysis.Jaynes stated Bayes' Rule was a way to calculate a probability, while Maximum Entropy was a way to assign a prior probability distribution (Jaynes 1988).
See also
- Entropy maximization
- Maximum entropy classifier
- Maximum entropy probability distributionMaximum entropy probability distributionIn statistics and information theory, a maximum entropy probability distribution is a probability distribution whose entropy is at least as great as that of all other members of a specified class of distributions....
- Maximum entropy spectral estimationMaximum entropy spectral estimationThe maximum entropy method applied to spectral density estimation. The overall idea is that the maximum entropy rate stochastic process that satisfies the given constant autocorrelation and variance constraints, is a linear Gauss-Markov process with i.i.d...
- Maximum entropy thermodynamicsMaximum entropy thermodynamicsIn physics, maximum entropy thermodynamics views equilibrium thermodynamics and statistical mechanics as inference processes. More specifically, MaxEnt applies inference techniques rooted in Shannon information theory, Bayesian probability, and the principle of maximum entropy...
Further reading
- Jaynes, E. T., 1986 (new version online 1996), 'Monkeys, kangaroos and
 ', in Maximum-Entropy and Bayesian Methods in Applied Statistics, J. H. Justice (ed.), Cambridge University Press, Cambridge, p. 26.
', in Maximum-Entropy and Bayesian Methods in Applied Statistics, J. H. Justice (ed.), Cambridge University Press, Cambridge, p. 26. - Bajkova, A. T., 1992, The generalization of maximum entropy method for reconstruction of complex functions. Astronomical and Astrophysical Transactions, V.1, issue 4, p. 313-320.
- Jaynes, E. T., 2003, Probability Theory: The Logic of Science, Cambridge University Press.
- Giffin, A. and Caticha, A., 2007, Updating Probabilities with Data and Moments
- Guiasu, S. and Shenitzer, A., 1985, 'The principle of maximum entropy', The Mathematical Intelligencer, 7(1), 42-48.
- Harremoës P. and Topsøe F., 2001, Maximum Entropy Fundamentals, Entropy, 3(3), 191-226.
- Kapur, J. N.; and Kesevan, H. K., 1992, Entropy optimization principles with applications, Boston: Academic Press. ISBN 0-12-397670-7
- Kitamura, Y., 2006, Empirical Likelihood Methods in Econometrics: Theory and Practice, Cowles Foundation Discussion Papers 1569, Cowles Foundation, Yale University.
- Lazar, N., 2003, "Bayesian Empirical Likelihood", Biometrika, 90, 319-326.
- Owen, A. B., Empirical Likelihood, Chapman and Hall.
- Schennach, S. M., 2005, "Bayesian Exponentially Tilted Empirical Likelihood", Biometrika, 92(1), 31-46.
- Uffink, Jos, 1995, 'Can the Maximum Entropy Principle be explained as a consistency requirement?', Studies in History and Philosophy of Modern Physics 26B, 223-261.
- Jaynes, E. T., 1988, 'The Relation of Bayesian and Maximum Entropy Methods', in Maximum-Entropy and Bayesian Methods in Science and Engineering (Vol. 1), Kluwer Academic Publishers, p. 25-26.
External links
- Ratnaparkhi A. "A simple introduction to maximum entropy models for natural language processing" Technical Report 97-08, Institute for Research in Cognitive Science, University of Pennsylvania, 1997. An easy-to-read introduction to maximum entropy methods in the context of natural language processing.
- Maximum Entropy Modeling
- A maximum entropy model applied to spatial and temporal correlations from cortical networks in vitro. This page contains pointers to various papers and software implementations of Maximum Entropy Model on the net.

