
Maximum entropy thermodynamics
Encyclopedia
In physics
, maximum entropy thermodynamics (colloquially, MaxEnt thermodynamics
) views equilibrium thermodynamics
and statistical mechanics
as inference processes. More specifically, MaxEnt applies inference techniques rooted in Shannon information theory, Bayesian probability
, and the principle of maximum entropy
. These techniques are relevant to any situation requiring prediction from incomplete or insufficient data (e.g., image reconstruction
, signal processing
, spectral analysis
, and inverse problem
s). MaxEnt thermodynamics began with two papers Edwin T. Jaynes
published in the 1957 Physical Review.
, which states that given certain "testable information" about a probability distribution
, for example particular expectation
values, but which is not in itself sufficient to uniquely determine the distribution, one should prefer the distribution which maximizes the Shannon information entropy.
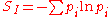
This is known as the Gibbs algorithm
, having been introduced by J. Willard Gibbs in 1878, to set up statistical ensembles to predict the properties of thermodynamic systems at equilibrium. It is the cornerstone of the statistical mechanical analysis of the thermodynamic properties of equilibrium systems (see partition function
).
A direct connection is thus made between the equilibrium thermodynamic entropy STh, a state function
of pressure, volume, temperature, etc., and the information entropy
for the predicted distribution with maximum uncertainty conditioned only on the expectation values of those variables:
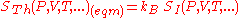
kB, Boltzmann's constant, has no fundamental physical significance here, but is necessary to retain consistency with the previous historical definition of entropy by Clausius (1865) (see Boltzmann's constant).
However, the MaxEnt school argue that the MaxEnt approach is a general technique of statistical inference, with applications far beyond this. It can therefore also be used to predict a distribution for "trajectories" Γ "over a period of time" by maximising:

This "information entropy" does not necessarily have a simple correspondence with thermodynamic entropy. But it can be used to predict features of nonequilibrium thermodynamic
systems as they evolve over time.
In the field of near-equilibrium thermodynamics, the Onsager reciprocal relations
and the Green-Kubo relations
fall out very directly. The approach also creates a solid theoretical framework for the study of far-from-equilibrium thermodynamics, making the derivation of the entropy production fluctuation theorem
particularly straightforward. Practical calculations for most far-from-equilibrium systems remain very challenging, however.
Technical note: For the reasons discussed in the article differential entropy
, the simple definition of Shannon entropy ceases to be directly applicable for random variable
s with continuous probability distribution function
s. Instead the appropriate quantity to maximise is the "relative information entropy,"

Hc is the negative of the Kullback-Leibler divergence, or discrimination information, of m(x) from p(x), where m(x) is a prior invariant measure
for the variable(s). The relative entropy Hc is always less than zero, and can be thought of as (the negative of) the number of bit
s of uncertainty lost by fixing on p(x) rather than m(x). Unlike the Shannon entropy, the relative entropy Hc has the advantage of remaining finite and well-defined for continuous x, and invariant under 1-to-1 coordinate transformations. The two expressions coincide for discrete probability distributions, if one can make the assumption that m(xi) is uniform - i.e. the principle of equal a-priori probability, which underlies statistical thermodynamics.
in thermodynamics. This position is sketched below.
); and by respectively specified particular partial descriptions of the system (the macroscopic description of the system used to constrain the MaxEnt probability assignment). The probabilities are objective
in the sense that, given these inputs, a uniquely defined probability distribution will result, independent of the subjectivity or arbitrary opinion of particular persons. The probabilities are epistemic in the sense that they are defined in terms of specified data and derived from those data by definite and objective rules of inference. Here the word epistemic, which refers to objective and impersonal scientific knowledge, is used in the sense that contrasts it with opiniative, which refers to the subjective or arbitrary beliefs of particular persons; this contrast was used by Plato
and Aristotle
and stands reliable today.
The probabilities represent both the degree of knowledge and lack of information in the data and the model used in the analyst's macroscopic description of the system, and also what those data say about the nature of the underlying reality.
The fitness of the probabilities depends on whether the constraints of the specified macroscopic model are a sufficiently accurate and/or complete description of the system to capture all of the experimentally reproducible behaviour. This cannot be guaranteed, a priori. For this reason MaxEnt proponents also call the method predictive statistical mechanics. The predictions can fail. But if they do, this is informative, because it signals the presence of new constraints needed to capture reproducible behaviour in the system, which had not been taken into account.
Of course, in reality there is only one real state of the system. The entropy is not a direct function of that state. It is a function of the real state only through the (subjectively chosen) macroscopic model description.
, despite the intense interest in them in the first part of the twentieth century, strictly speaking are not relevant to the probability assignment for the state one might find the system in.
However, this changes if there is additional knowledge that the system is being prepared in a particular way some time before the measurement. One must then consider whether this gives further information which is still relevant at the time of measurement. The question of how 'rapidly mixing' different properties of the system are then becomes very much of interest. Information about some degrees of freedom of the combined system may become unusable very quickly; information about other properties of the system may go on being relevant for a considerable time.
If nothing else, the medium and long-run time correlation properties of the system are interesting subjects for experimentation in themselves. Failure to accurately predict them is a good indicator that relevant macroscopically determinable physics may be missing from the model.
for Hamiltonian dynamics, the hyper-volume of a cloud of points in phase space
remains constant as the system evolves. Therefore, the information entropy must also remain constant, if we condition on the original information, and then follow each of those microstates forward in time:
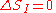
However, as time evolves, that initial information we had becomes less directly accessible. Instead of being easily summarisable in the macroscopic description of the system, it increasingly relates to very subtle correlations between the positions and momenta of individual molecules. (Compare to Boltzmann's H-theorem
.) Equivalently, it means that the probability distribution for the whole system, in 6N-dimensional phase space, becomes increasingly irregular, spreading out into long thin fingers rather than the initial tightly defined volume of possibilities.
Classical thermodynamics is built on the assumption that entropy is a state function
of the macroscopic variables -- i.e., that none of the history of the system matters, so that it can all be ignored.
The extended, wispy, evolved probability distribution, which still has the initial Shannon entropy STh(1), should reproduce the expectation values of the observed macroscopic variables at time t2. However it will no longer necessarily be a maximum entropy distribution for that new macroscopic description. On the other hand, the new thermodynamic entropy STh(2) assuredly will measure the maximum entropy distribution, by construction. Therefore, we expect:

At an abstract level, this result simply means that some of the information we originally had about the system has become "no longer useful" at a macroscopic level. At the level of the 6N-dimensional probability distribution, this result represents coarse graining -- i.e., information loss by smoothing out very fine-scale detail.
1. Like all statistical mechanical results according to the MaxEnt school, this increase in thermodynamic entropy is only a prediction. It assumes in particular that the initial macroscopic description contains all of the information relevant to predicting the later macroscopic state. This may not be the case, for example if the initial description fails to reflect some aspect of the preparation of the system which later becomes relevant. In that case the "failure" of a MaxEnt prediction tells us that there is something more which is relevant that we may have overlooked in the physics of the system.
It is also sometimes suggested that quantum measurement, especially in the decoherence interpretation, may give an apparently unexpected reduction in entropy per this argument, as it appears to involve macroscopic information becoming available which was previously inaccessible. (However, the entropy accounting of quantum measurement is tricky, because to get full decoherence one may be assuming an infinite environment, with an infinite entropy).
2. The argument so far has glossed over the question of fluctuations. It has also implicitly assumed that the uncertainty predicted at time t1 for the variables at time t2 will be much smaller than the measurement error. But if the measurements do meaningfully update our knowledge of the system, our uncertainty as to its state is reduced, giving a new SI(2) which is less than SI(1). (Note that if we allow ourselves the abilities of Laplace's demon
, the consequences of this new information can also be mapped backwards, so our uncertainty about the dynamical state at time t1 is now also reduced from SI(1) to SI(2) ).
We know that STh(2) > SI(2); but we can now no longer be certain that it is greater than STh(1) = SI(1). This then leaves open the possibility for fluctuations in STh. The thermodynamic entropy may go "down" as well as up. A more sophisticated analysis is given by the entropy Fluctuation Theorem
, which can be established as a consequence of the time-dependent MaxEnt picture.
3. As just indicated, the MaxEnt inference runs equally well in reverse. So given a particular final state, we can ask, what can we "retrodict" to improve our knowledge about earlier states? However the Second Law argument above also runs in reverse: given macroscopic information at time t2, we should expect it too to become less useful. The two procedures are time-symmetric. But now the information will become less and less useful at earlier and earlier times. (Compare with Loschmidt's paradox
.) The MaxEnt inference would predict that the most probable origin of a currently low-entropy state would be as a spontaneous fluctuation from an earlier high entropy state. But this conflicts with what we know to have happened, namely that entropy has been increasing steadily, even back in the past.
The MaxEnt proponents' response to this would be that such a systematic failing in the prediction of a MaxEnt inference is a "good" thing. It means that there is thus clear evidence that some important physical information has been missed in the specification the problem. If it is correct that the dynamics "are" time-symmetric
, it appears that we need to put in by hand a prior probability
that initial configurations with a low thermodynamic entropy are more likely than initial configurations with a high thermodynamic entropy. This cannot be explained by the immediate dynamics. Quite possibly, it arises as a reflection of the evident time-asymmetric evolution of the universe on a cosmological scale (see arrow of time
).
The theory has also been criticized in the grounds of internal consistency. For instance, Radu Balescu
provides a concise but strong criticism of the MaxEnt School and of Jaynes' work. Balescu states how Jaynes' and coworkers theory is based on a non-transitive evolution law that produces ambiguous results. Although some difficulties of the theory can be cured, the theory "lacks a solid foundation" and "has not led to any new concrete result".
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, maximum entropy thermodynamics (colloquially, MaxEnt thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
) views equilibrium thermodynamics
Equilibrium thermodynamics
Equilibrium Thermodynamics is the systematic study of transformations of matter and energy in systems as they approach equilibrium. The word equilibrium implies a state of balance. Equilibrium thermodynamics, in origins, derives from analysis of the Carnot cycle. Here, typically a system, as...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
as inference processes. More specifically, MaxEnt applies inference techniques rooted in Shannon information theory, Bayesian probability
Bayesian probability
Bayesian probability is one of the different interpretations of the concept of probability and belongs to the category of evidential probabilities. The Bayesian interpretation of probability can be seen as an extension of logic that enables reasoning with propositions, whose truth or falsity is...
, and the principle of maximum entropy
Principle of maximum entropy
In Bayesian probability, the principle of maximum entropy is a postulate which states that, subject to known constraints , the probability distribution which best represents the current state of knowledge is the one with largest entropy.Let some testable information about a probability distribution...
. These techniques are relevant to any situation requiring prediction from incomplete or insufficient data (e.g., image reconstruction
Image processing
In electrical engineering and computer science, image processing is any form of signal processing for which the input is an image, such as a photograph or video frame; the output of image processing may be either an image or, a set of characteristics or parameters related to the image...
, signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
, spectral analysis
Spectral analysis
Spectral analysis or Spectrum analysis may refer to:* Spectrum analysis in chemistry and physics, a method of analyzing the chemical properties of matter from bands in their visible spectrum...
, and inverse problem
Inverse problem
An inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in...
s). MaxEnt thermodynamics began with two papers Edwin T. Jaynes
Edwin Thompson Jaynes
Edwin Thompson Jaynes was Wayman Crow Distinguished Professor of Physics at Washington University in St. Louis...
published in the 1957 Physical Review.
Maximum Shannon entropy
Central to the MaxEnt thesis is the principle of maximum entropyPrinciple of maximum entropy
In Bayesian probability, the principle of maximum entropy is a postulate which states that, subject to known constraints , the probability distribution which best represents the current state of knowledge is the one with largest entropy.Let some testable information about a probability distribution...
, which states that given certain "testable information" about a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
, for example particular expectation
Expectation
In the case of uncertainty, expectation is what is considered the most likely to happen. An expectation, which is a belief that is centered on the future, may or may not be realistic. A less advantageous result gives rise to the emotion of disappointment. If something happens that is not at all...
values, but which is not in itself sufficient to uniquely determine the distribution, one should prefer the distribution which maximizes the Shannon information entropy.
This is known as the Gibbs algorithm
Gibbs algorithm
In statistical mechanics, the Gibbs algorithm, first introduced by J. Willard Gibbs in 1878, is the injunction to choose a statistical ensemble for the unknown microscopic state of a thermodynamic system by minimising the average log probability H = \sum_i p_i \ln p_i \, subject to the probability...
, having been introduced by J. Willard Gibbs in 1878, to set up statistical ensembles to predict the properties of thermodynamic systems at equilibrium. It is the cornerstone of the statistical mechanical analysis of the thermodynamic properties of equilibrium systems (see partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
).
A direct connection is thus made between the equilibrium thermodynamic entropy STh, a state function
State function
In thermodynamics, a state function, function of state, state quantity, or state variable is a property of a system that depends only on the current state of the system, not on the way in which the system acquired that state . A state function describes the equilibrium state of a system...
of pressure, volume, temperature, etc., and the information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
for the predicted distribution with maximum uncertainty conditioned only on the expectation values of those variables:
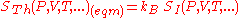
kB, Boltzmann's constant, has no fundamental physical significance here, but is necessary to retain consistency with the previous historical definition of entropy by Clausius (1865) (see Boltzmann's constant).
However, the MaxEnt school argue that the MaxEnt approach is a general technique of statistical inference, with applications far beyond this. It can therefore also be used to predict a distribution for "trajectories" Γ "over a period of time" by maximising:

This "information entropy" does not necessarily have a simple correspondence with thermodynamic entropy. But it can be used to predict features of nonequilibrium thermodynamic
Non-equilibrium thermodynamics
Non-equilibrium thermodynamics is a branch of thermodynamics that deals with systems that are not in thermodynamic equilibrium. Most systems found in nature are not in thermodynamic equilibrium; for they are changing or can be triggered to change over time, and are continuously and discontinuously...
systems as they evolve over time.
In the field of near-equilibrium thermodynamics, the Onsager reciprocal relations
Onsager reciprocal relations
In thermodynamics, the Onsager reciprocal relations express the equality of certain ratios between flows and forces in thermodynamic systems out of equilibrium, but where a notion of local equilibrium exists....
and the Green-Kubo relations
Green-Kubo relations
The Green–Kubo relations give the exact mathematical expression for transport coefficients in terms of integrals of time correlation functions.-Thermal and mechanical transport processes:...
fall out very directly. The approach also creates a solid theoretical framework for the study of far-from-equilibrium thermodynamics, making the derivation of the entropy production fluctuation theorem
Fluctuation theorem
The fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
particularly straightforward. Practical calculations for most far-from-equilibrium systems remain very challenging, however.
Technical note: For the reasons discussed in the article differential entropy
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
, the simple definition of Shannon entropy ceases to be directly applicable for random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s with continuous probability distribution function
Probability distribution function
Depending upon which text is consulted, a probability distribution function is any of:* a probability distribution function,* a cumulative distribution function,* a probability mass function, or* a probability density function....
s. Instead the appropriate quantity to maximise is the "relative information entropy,"

Hc is the negative of the Kullback-Leibler divergence, or discrimination information, of m(x) from p(x), where m(x) is a prior invariant measure
Invariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
for the variable(s). The relative entropy Hc is always less than zero, and can be thought of as (the negative of) the number of bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
s of uncertainty lost by fixing on p(x) rather than m(x). Unlike the Shannon entropy, the relative entropy Hc has the advantage of remaining finite and well-defined for continuous x, and invariant under 1-to-1 coordinate transformations. The two expressions coincide for discrete probability distributions, if one can make the assumption that m(xi) is uniform - i.e. the principle of equal a-priori probability, which underlies statistical thermodynamics.
Philosophical Implications
Adherents to the MaxEnt viewpoint take a clear position on some of the conceptual/philosophical questionsPhilosophy of thermal and statistical physics
The philosophy of thermal and statistical physics is that part of the philosophy of physics whose subject matter is classical thermodynamics, statistical mechanics, and related theories...
in thermodynamics. This position is sketched below.
The nature of the probabilities in statistical mechanics
Jaynes (1985, 2003, et passim) discussed the concept of probability. According to the MaxEnt viewpoint, the probabilities in statistical mechanics are determined jointly by two factors: by respectively specified particular models for the underlying state space (e.g. Liouvillian phase spacePhase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
); and by respectively specified particular partial descriptions of the system (the macroscopic description of the system used to constrain the MaxEnt probability assignment). The probabilities are objective
Objectivity (science)
Objectivity in science is a value that informs how science is practiced and how scientific truths are created. It is the idea that scientists, in attempting to uncover truths about the natural world, must aspire to eliminate personal biases, a priori commitments, emotional involvement, etc...
in the sense that, given these inputs, a uniquely defined probability distribution will result, independent of the subjectivity or arbitrary opinion of particular persons. The probabilities are epistemic in the sense that they are defined in terms of specified data and derived from those data by definite and objective rules of inference. Here the word epistemic, which refers to objective and impersonal scientific knowledge, is used in the sense that contrasts it with opiniative, which refers to the subjective or arbitrary beliefs of particular persons; this contrast was used by Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
and Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
and stands reliable today.
The probabilities represent both the degree of knowledge and lack of information in the data and the model used in the analyst's macroscopic description of the system, and also what those data say about the nature of the underlying reality.
The fitness of the probabilities depends on whether the constraints of the specified macroscopic model are a sufficiently accurate and/or complete description of the system to capture all of the experimentally reproducible behaviour. This cannot be guaranteed, a priori. For this reason MaxEnt proponents also call the method predictive statistical mechanics. The predictions can fail. But if they do, this is informative, because it signals the presence of new constraints needed to capture reproducible behaviour in the system, which had not been taken into account.
Is entropy "real" ?
The thermodynamic entropy (at equilibrium) is a function of the state variables of the model description. It is therefore as "real" as the other variables in the model description. If the model constraints in the probability assignment are a "good" description, containing all the information needed to predict reproducible experimental results, then that includes all of the results one could predict using the formulae involving entropy from classical thermodynamics. To that extent, the MaxEnt STh is as "real" as the entropy in classical thermodynamics.Of course, in reality there is only one real state of the system. The entropy is not a direct function of that state. It is a function of the real state only through the (subjectively chosen) macroscopic model description.
Is ergodic theory relevant ?
The Gibbsian ensemble idealises the notion of repeating an experiment again and again on different systems, not again and again on the same system. So long-term time averages and the ergodic hypothesisErgodic hypothesis
In physics and thermodynamics, the ergodic hypothesis says that, over long periods of time, the time spent by a particle in some region of the phase space of microstates with the same energy is proportional to the volume of this region, i.e., that all accessible microstates are equiprobable over a...
, despite the intense interest in them in the first part of the twentieth century, strictly speaking are not relevant to the probability assignment for the state one might find the system in.
However, this changes if there is additional knowledge that the system is being prepared in a particular way some time before the measurement. One must then consider whether this gives further information which is still relevant at the time of measurement. The question of how 'rapidly mixing' different properties of the system are then becomes very much of interest. Information about some degrees of freedom of the combined system may become unusable very quickly; information about other properties of the system may go on being relevant for a considerable time.
If nothing else, the medium and long-run time correlation properties of the system are interesting subjects for experimentation in themselves. Failure to accurately predict them is a good indicator that relevant macroscopically determinable physics may be missing from the model.
The Second Law
According to Liouville's theoremLiouville's theorem (Hamiltonian)
In physics, Liouville's theorem, named after the French mathematician Joseph Liouville, is a key theorem in classical statistical and Hamiltonian mechanics...
for Hamiltonian dynamics, the hyper-volume of a cloud of points in phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
remains constant as the system evolves. Therefore, the information entropy must also remain constant, if we condition on the original information, and then follow each of those microstates forward in time:
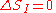
However, as time evolves, that initial information we had becomes less directly accessible. Instead of being easily summarisable in the macroscopic description of the system, it increasingly relates to very subtle correlations between the positions and momenta of individual molecules. (Compare to Boltzmann's H-theorem
H-theorem
In Classical Statistical Mechanics, the H-theorem, introduced by Ludwig Boltzmann in 1872, describes the increase in the entropy of an ideal gas in an irreversible process. H-theorem follows from considerations of Boltzmann's equation...
.) Equivalently, it means that the probability distribution for the whole system, in 6N-dimensional phase space, becomes increasingly irregular, spreading out into long thin fingers rather than the initial tightly defined volume of possibilities.
Classical thermodynamics is built on the assumption that entropy is a state function
State function
In thermodynamics, a state function, function of state, state quantity, or state variable is a property of a system that depends only on the current state of the system, not on the way in which the system acquired that state . A state function describes the equilibrium state of a system...
of the macroscopic variables -- i.e., that none of the history of the system matters, so that it can all be ignored.
The extended, wispy, evolved probability distribution, which still has the initial Shannon entropy STh(1), should reproduce the expectation values of the observed macroscopic variables at time t2. However it will no longer necessarily be a maximum entropy distribution for that new macroscopic description. On the other hand, the new thermodynamic entropy STh(2) assuredly will measure the maximum entropy distribution, by construction. Therefore, we expect:

At an abstract level, this result simply means that some of the information we originally had about the system has become "no longer useful" at a macroscopic level. At the level of the 6N-dimensional probability distribution, this result represents coarse graining -- i.e., information loss by smoothing out very fine-scale detail.
Caveats with the argument
Some caveats should be considered with the above.1. Like all statistical mechanical results according to the MaxEnt school, this increase in thermodynamic entropy is only a prediction. It assumes in particular that the initial macroscopic description contains all of the information relevant to predicting the later macroscopic state. This may not be the case, for example if the initial description fails to reflect some aspect of the preparation of the system which later becomes relevant. In that case the "failure" of a MaxEnt prediction tells us that there is something more which is relevant that we may have overlooked in the physics of the system.
It is also sometimes suggested that quantum measurement, especially in the decoherence interpretation, may give an apparently unexpected reduction in entropy per this argument, as it appears to involve macroscopic information becoming available which was previously inaccessible. (However, the entropy accounting of quantum measurement is tricky, because to get full decoherence one may be assuming an infinite environment, with an infinite entropy).
2. The argument so far has glossed over the question of fluctuations. It has also implicitly assumed that the uncertainty predicted at time t1 for the variables at time t2 will be much smaller than the measurement error. But if the measurements do meaningfully update our knowledge of the system, our uncertainty as to its state is reduced, giving a new SI(2) which is less than SI(1). (Note that if we allow ourselves the abilities of Laplace's demon
Laplace's demon
In the history of science, Laplace's demon was the first published articulation of causal or scientific determinism by Pierre-Simon Laplace in 1814...
, the consequences of this new information can also be mapped backwards, so our uncertainty about the dynamical state at time t1 is now also reduced from SI(1) to SI(2) ).
We know that STh(2) > SI(2); but we can now no longer be certain that it is greater than STh(1) = SI(1). This then leaves open the possibility for fluctuations in STh. The thermodynamic entropy may go "down" as well as up. A more sophisticated analysis is given by the entropy Fluctuation Theorem
Fluctuation theorem
The fluctuation theorem , which originated from statistical mechanics, deals with the relative probability that the entropy of a system which is currently away from thermodynamic equilibrium will increase or decrease over a given amount of time...
, which can be established as a consequence of the time-dependent MaxEnt picture.
3. As just indicated, the MaxEnt inference runs equally well in reverse. So given a particular final state, we can ask, what can we "retrodict" to improve our knowledge about earlier states? However the Second Law argument above also runs in reverse: given macroscopic information at time t2, we should expect it too to become less useful. The two procedures are time-symmetric. But now the information will become less and less useful at earlier and earlier times. (Compare with Loschmidt's paradox
Loschmidt's paradox
Loschmidt's paradox, also known as the reversibility paradox, is the objection that it should not be possible to deduce an irreversible process from time-symmetric dynamics...
.) The MaxEnt inference would predict that the most probable origin of a currently low-entropy state would be as a spontaneous fluctuation from an earlier high entropy state. But this conflicts with what we know to have happened, namely that entropy has been increasing steadily, even back in the past.
The MaxEnt proponents' response to this would be that such a systematic failing in the prediction of a MaxEnt inference is a "good" thing. It means that there is thus clear evidence that some important physical information has been missed in the specification the problem. If it is correct that the dynamics "are" time-symmetric
T-symmetry
T Symmetry is the symmetry of physical laws under a time reversal transformation: T: t \mapsto -t.Although in restricted contexts one may find this symmetry, the observable universe itself does not show symmetry under time reversal, primarily due to the second law of thermodynamics.Time asymmetries...
, it appears that we need to put in by hand a prior probability
Prior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
that initial configurations with a low thermodynamic entropy are more likely than initial configurations with a high thermodynamic entropy. This cannot be explained by the immediate dynamics. Quite possibly, it arises as a reflection of the evident time-asymmetric evolution of the universe on a cosmological scale (see arrow of time
Arrow of time
The arrow of time, or time’s arrow, is a term coined in 1927 by the British astronomer Arthur Eddington to describe the "one-way direction" or "asymmetry" of time...
).
Criticisms
Maximum Entropy thermodynamics has generally failed to be accepted by the majority of scientists, with mainstream thermodynamicists considering Jaynes' work as an unfounded mathematical contrivance. This is in part because of the relative paucity of published results from the MaxEnt school, especially with regard to the new testable predictions far-from-equilibrium.The theory has also been criticized in the grounds of internal consistency. For instance, Radu Balescu
Radu Balescu
Radu Bălescu was a Romanian and Belgian scientist and professor at the Statistical and Plasma Physics group of the Université Libre de Bruxelles ....
provides a concise but strong criticism of the MaxEnt School and of Jaynes' work. Balescu states how Jaynes' and coworkers theory is based on a non-transitive evolution law that produces ambiguous results. Although some difficulties of the theory can be cured, the theory "lacks a solid foundation" and "has not led to any new concrete result".
Further Reading
Shows invalidity of Dewar's derivations (a) of maximum entropy production (MaxEP) from fluctuation theorem for far-from-equilibrium systems, and (b) of a claimed link between MaxEP and self-organized criticality.- Grandy, W. T., 1987. Foundations of Statistical Mechanics. Vol 1: Equilibrium Theory; Vol. 2: Nonequilibrium Phenomena. Dordrecht: D. Reidel. Vol. 1: ISBN 90-277-2489-X. Vol. 2: ISBN 90-277-2649-3.
- Extensive archive of further papers by E.T. Jaynes on probability and physics. Many are collected in

