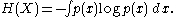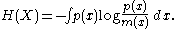Limiting density of discrete points
Encyclopedia
In information theory
, the limiting density of discrete points is an adjustment to the formula of Claude Elwood Shannon
for differential entropy
.
It was formulated by Edwin Thompson Jaynes
to address defects in the initial definition of differential entropy.
of a continuous distribution, known as differential entropy:
Unlike Shannon's formula for the discrete entropy, however, this is not the result of any derivation (Shannon simply replaced the summation symbol in the discrete version with an integral) and it turns out to lack many of the properties that make the discrete entropy a useful measure of uncertainty. In particular, it is not invariant under a change of variables
and can even become negative.
Jaynes (1963, 1968) argued that the formula for the continuous entropy should be derived by taking the limit of increasingly dense discrete distributions. Suppose that we have a set of
discrete points 
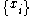, such that in the limit 
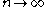their density approaches a function 
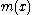called the invariant measure
.
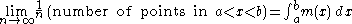
Jaynes derived from this the following formula for the continuous entropy, which he argued should be taken as the correct formula:
It is formally similar to but conceptually distinct from the (negative of the) Kullback–Leibler divergence
or relative entropy, which is comparison measure between two probability distributions. The formula for the Kullback-Leibler divergence is similar, except that the invariant measure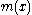
is replaced by a second probability density function 
. In Jaynes' formula, 
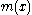is not a probability density but simply a density. In particular it does not have to be normalised so as to sum to 1.
Jaynes' continuous entropy formula and the relative entropy share the property of being invariant under a change of variables, which solves many of the difficulties that come from applying Shannon's continuous entropy formula.
It is the inclusion of the invariant measure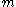
that ensures the formula's invariance under a change of variables, since both 
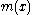and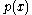 
must be transformed in the same way.
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
, the limiting density of discrete points is an adjustment to the formula of Claude Elwood Shannon
Claude Elwood Shannon
Claude Elwood Shannon was an American mathematician, electronic engineer, and cryptographer known as "the father of information theory"....
for differential entropy
Differential entropy
Differential entropy is a concept in information theory that extends the idea of entropy, a measure of average surprisal of a random variable, to continuous probability distributions.-Definition:...
.
It was formulated by Edwin Thompson Jaynes
Edwin Thompson Jaynes
Edwin Thompson Jaynes was Wayman Crow Distinguished Professor of Physics at Washington University in St. Louis...
to address defects in the initial definition of differential entropy.
Definition
Shannon originally wrote down the following formula for the entropyEntropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
of a continuous distribution, known as differential entropy:
Unlike Shannon's formula for the discrete entropy, however, this is not the result of any derivation (Shannon simply replaced the summation symbol in the discrete version with an integral) and it turns out to lack many of the properties that make the discrete entropy a useful measure of uncertainty. In particular, it is not invariant under a change of variables
Change of variables
In mathematics, a change of variables is a basic technique used to simplify problems in which the original variables are replaced with new ones; the new and old variables being related in some specified way...
and can even become negative.
Jaynes (1963, 1968) argued that the formula for the continuous entropy should be derived by taking the limit of increasingly dense discrete distributions. Suppose that we have a set of
discrete points 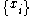, such that in the limit 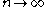their density approaches a function 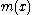called the invariant measureInvariant measure
In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...
.
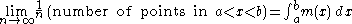
Jaynes derived from this the following formula for the continuous entropy, which he argued should be taken as the correct formula:
It is formally similar to but conceptually distinct from the (negative of the) Kullback–Leibler divergence
Kullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
or relative entropy, which is comparison measure between two probability distributions. The formula for the Kullback-Leibler divergence is similar, except that the invariant measure
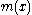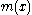is replaced by a second probability density function . In Jaynes' formula, is not a probability density but simply a density. In particular it does not have to be normalised so as to sum to 1.Jaynes' continuous entropy formula and the relative entropy share the property of being invariant under a change of variables, which solves many of the difficulties that come from applying Shannon's continuous entropy formula.
It is the inclusion of the invariant measure
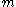that ensures the formula's invariance under a change of variables, since both 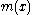and 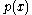must be transformed in the same way.