
Price index
Encyclopedia
A price index is a normalized average
(typically a weighted average
) of price
s for a given class of goods or services in a given region, during a given interval of time. It is a statistic
designed to help to compare how these prices, taken as a whole, differ between time periods or geographical locations.
Price indices have several potential uses. For particularly broad indices, the index can be said to measure the economy's price level
or a cost of living. More narrow price indices can help producers with business plans and pricing. Sometimes, they can be useful in helping to guide investment.
Some notable price indices include:
Rice Vaughan who examined price level change in his 1675 book A Discourse of Coin and Coinage. Vaughan wanted to separate the inflationary impact of the influx of precious metals brought by Spain
from the New World
from the effect due to currency debasement
. Vaughan compared labor statutes from his own time to similar statutes
dating back to Edward III. These statutes set wages for certain tasks and provided a good record of the change in wage levels. Vaughan reasoned that the market for basic labor did not fluctuate much with time and that a basic laborers salary would probably buy the same amount of goods in different time periods, so that a laborer's salary acted as a basket of goods. Vaughan's analysis indicated that price levels in England had risen six to eightfold over the preceding century.
While Vaughan can be considered a forerunner of price index research, his analysis did not actually involve calculating an index. In 1707 Englishman William Fleetwood
created perhaps the first true price index. An Oxford student asked Fleetwood to help show how prices had changed. The student stood to lose his fellowship since a fifteenth century stipulation barred students with annual incomes over five pounds from receiving a fellowship. Fleetwood, who already had an interest in price change, had collected a large amount of price data going back hundreds of years. Fleetwood proposed an index consisting of averaged price relatives and used his methods to show that the value of five pounds had changed greatly over the course of 260 years. He argued on behalf of the Oxford students and published his findings anonymously in a volume entitled Chronicon Preciosum.
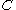 of goods and services, the total market value of transactions in
of goods and services, the total market value of transactions in  in some period
in some period  would be
would be
where represents the prevailing price of
represents the prevailing price of  in period
in period 
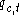 represents the quantity of
represents the quantity of  sold in period
sold in period 
If, across two periods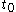 and
and  , the same quantities of each good or service were sold, but under different prices, then
, the same quantities of each good or service were sold, but under different prices, then
and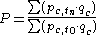
would be a reasonable measure
of the price of the set in one period relative to that in the other, and would provide an index
measuring relative prices overall, weighted by quantities sold.
Of course, for any practical purpose, quantities purchased are rarely if ever identical across any two periods. As such, this is not a very practical index formula.
One might be tempted to modify the formula slightly to

This new index, however, doesn't do anything to distinguish growth or reduction in quantities sold from price changes. To see that this is so, consider what happens if all the prices double between and
and  while quantities stay the same:
while quantities stay the same:  will double. Now consider what happens if all the quantities double between
will double. Now consider what happens if all the quantities double between  and
and 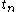 while all the prices stay the same:
while all the prices stay the same:  will double. In either case the change in
will double. In either case the change in  is identical. As such,
is identical. As such,  is as much a quantity index as it is a price index.
is as much a quantity index as it is a price index.
Various indices have been constructed in an attempt to compensate for this difficulty.
ˈpaːʃɛ) and the Laspeyres index (after the German economist
Etienne Laspeyres
lasˈpejres).
The Paasche index is computed as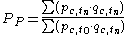
while the Laspeyres index is computed as
where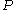 is the relative index of the price levels in two periods,
is the relative index of the price levels in two periods,  is the base period (usually the first year), and
is the base period (usually the first year), and  the period for which the index is computed.
the period for which the index is computed.
Note that the only difference in the formulas is that the former uses period n quantities, whereas the latter uses base period (period 0) quantities.
When applied to bundles of individual consumers, a Laspeyres index of 1 would state that an agent in the current period can afford to buy the same bundle as he consumed in the previous period, given that income has not changed; a Paasche index of 1 would state that an agent could have consumed the same bundle in the base period as she is consuming in the current period, given that income has not changed.
Hence, one may think of the Laspeyres index as one where the numeraire
is the bundle of goods using current year prices but base year quantities. Similarly, the Paasche index can be thought of as a price index taking the bundle of goods using current prices and current quantities as the numeraire.
The Laspeyres index tends to overstate inflation (in a cost of living framework), while the Paasche index tends to understate it, because the indices do not account for the fact that consumers typically react to price changes by changing the quantities that they buy. For example, if prices go up for good then, ceteris paribus
then, ceteris paribus
, quantities of that good should go down.
and Francis Ysidro Edgeworth
), tries to overcome these problems of under- and overstatement by using the arithmetic means of the quantities: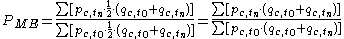
A fourth, the Fisher index (after the American economist Irving Fisher
), is calculated as the geometric mean
of and
and  :
: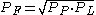
Fisher's index is also known as the “ideal” price index.
However, there is no guarantee with either the Marshall–Edgeworth index or the Fisher index that the overstatement and understatement will exactly cancel the other.
While these indices were introduced to provide overall measurement
of relative prices, there is ultimately no way of measuring the imperfections of any of these indices (Paasche, Laspeyres, Fisher, or Marshall–Edgeworth) against reality.
, number values that indicate relative change but not absolute values (i.e. one price index value can be compared to another or a base, but the number alone has no meaning). Price indices generally select a base year and make that index value equal to 100. You then express every other year as a percentage of that base year. In our example above, let's take 2000 as our base year. The value of our index will be 100. The price
When an index has been normalized in this manner, the meaning of the number 108, for instance, is that the total cost for the basket of goods is 4% more in 2001, 8% more in 2002 and 12% more in 2003 than in the base year (in this case, year 2000).
Here is a reformulation for the Laspeyres index:
Let be the total expenditure on good c in the base period, then (by definition) we have
be the total expenditure on good c in the base period, then (by definition) we have

and therefore also
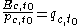 .
.
We can substitute these values into our Laspeyres formula as follows:
A similar transformation can be made for any index.
 is the period for which we wish to calculate the index and
is the period for which we wish to calculate the index and  is a reference period that anchors the value of the series:
is a reference period that anchors the value of the series:

Each term

answers the question "by what factor have prices increased between period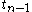 and period
and period  ". When you multiply these all together, you get the answer to the question "by what factor have prices increased since period
". When you multiply these all together, you get the answer to the question "by what factor have prices increased since period  ".
".
Nonetheless, note that, when chain indices are in use, the numbers cannot be said to be "in period " prices.
" prices.
 , where
, where 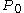 and
and 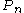 are vectors giving prices for a base period and a reference period while
are vectors giving prices for a base period and a reference period while  and
and  give quantities for these periods.
give quantities for these periods.
The problem discussed above can be represented as attempting to bridge the gap between the price for the old item in time t,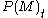 , with the price of the new item in the later time period,
, with the price of the new item in the later time period,  .
.
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
(typically a weighted average
Weighted mean
The weighted mean is similar to an arithmetic mean , where instead of each of the data points contributing equally to the final average, some data points contribute more than others...
) of price
Price
-Definition:In ordinary usage, price is the quantity of payment or compensation given by one party to another in return for goods or services.In modern economies, prices are generally expressed in units of some form of currency...
s for a given class of goods or services in a given region, during a given interval of time. It is a statistic
Statistic
A statistic is a single measure of some attribute of a sample . It is calculated by applying a function to the values of the items comprising the sample which are known together as a set of data.More formally, statistical theory defines a statistic as a function of a sample where the function...
designed to help to compare how these prices, taken as a whole, differ between time periods or geographical locations.
Price indices have several potential uses. For particularly broad indices, the index can be said to measure the economy's price level
Price level
A price level is a hypothetical measure of overall prices for some set of goods and services, in a given region during a given interval, normalized relative to some base set...
or a cost of living. More narrow price indices can help producers with business plans and pricing. Sometimes, they can be useful in helping to guide investment.
Some notable price indices include:
- Consumer price indexConsumer price indexA consumer price index measures changes in the price level of consumer goods and services purchased by households. The CPI, in the United States is defined by the Bureau of Labor Statistics as "a measure of the average change over time in the prices paid by urban consumers for a market basket of...
- Producer price indexProducer price indexA Producer Price Index measures average changes in prices received by domestic producers for their output. It is one of several price indices.Its importance is being undermined by the steady decline in manufactured goods as a share of spending....
- GDP deflatorGDP deflatorIn economics, the GDP deflator is a measure of the level of prices of all new, domestically produced, final goods and services in an economy...
History of early price indices
No clear consensus has emerged on who created the first price index. The earliest reported research in this area came from WelshmanWales
Wales is a country that is part of the United Kingdom and the island of Great Britain, bordered by England to its east and the Atlantic Ocean and Irish Sea to its west. It has a population of three million, and a total area of 20,779 km²...
Rice Vaughan who examined price level change in his 1675 book A Discourse of Coin and Coinage. Vaughan wanted to separate the inflationary impact of the influx of precious metals brought by Spain
Spain
Spain , officially the Kingdom of Spain languages]] under the European Charter for Regional or Minority Languages. In each of these, Spain's official name is as follows:;;;;;;), is a country and member state of the European Union located in southwestern Europe on the Iberian Peninsula...
from the New World
New World
The New World is one of the names used for the Western Hemisphere, specifically America and sometimes Oceania . The term originated in the late 15th century, when America had been recently discovered by European explorers, expanding the geographical horizon of the people of the European middle...
from the effect due to currency debasement
Debasement
Debasement is the practice of lowering the value of currency. It is particularly used in connection with commodity money such as gold or silver coins...
. Vaughan compared labor statutes from his own time to similar statutes
Statute of Labourers of 1351
The Statute of Labourers was a law enacted by the English parliament under King Edward III in 1351 in response to a labour shortage, designed to stabilize the labor force by prohibiting increases in wages and prohibiting the movement of workers from their home areas in search of improved conditions...
dating back to Edward III. These statutes set wages for certain tasks and provided a good record of the change in wage levels. Vaughan reasoned that the market for basic labor did not fluctuate much with time and that a basic laborers salary would probably buy the same amount of goods in different time periods, so that a laborer's salary acted as a basket of goods. Vaughan's analysis indicated that price levels in England had risen six to eightfold over the preceding century.
While Vaughan can be considered a forerunner of price index research, his analysis did not actually involve calculating an index. In 1707 Englishman William Fleetwood
William Fleetwood
William Fleetwood was an English preacher, Bishop of St Asaph and Bishop of Ely, remembered by economists and statisticians for constructing a price index in his Chronicon Preciosum of 1707.-Life:...
created perhaps the first true price index. An Oxford student asked Fleetwood to help show how prices had changed. The student stood to lose his fellowship since a fifteenth century stipulation barred students with annual incomes over five pounds from receiving a fellowship. Fleetwood, who already had an interest in price change, had collected a large amount of price data going back hundreds of years. Fleetwood proposed an index consisting of averaged price relatives and used his methods to show that the value of five pounds had changed greatly over the course of 260 years. He argued on behalf of the Oxford students and published his findings anonymously in a volume entitled Chronicon Preciosum.
Formal calculation
Given a set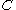 of goods and services, the total market value of transactions in
of goods and services, the total market value of transactions in  in some period
in some period  would be
would be
where
 represents the prevailing price of
represents the prevailing price of  in period
in period 
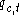 represents the quantity of
represents the quantity of  sold in period
sold in period 
If, across two periods
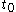 and
and  , the same quantities of each good or service were sold, but under different prices, then
, the same quantities of each good or service were sold, but under different prices, then
and
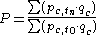
would be a reasonable measure
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
of the price of the set in one period relative to that in the other, and would provide an index
Index (mathematics)
The word index is used in variety of senses in mathematics.- General :* In perhaps the most frequent sense, an index is a number or other symbol that indicates the location of a variable in a list or array of numbers or other mathematical objects. This type of index is usually written as a...
measuring relative prices overall, weighted by quantities sold.
Of course, for any practical purpose, quantities purchased are rarely if ever identical across any two periods. As such, this is not a very practical index formula.
One might be tempted to modify the formula slightly to

This new index, however, doesn't do anything to distinguish growth or reduction in quantities sold from price changes. To see that this is so, consider what happens if all the prices double between
 and
and  while quantities stay the same:
while quantities stay the same:  will double. Now consider what happens if all the quantities double between
will double. Now consider what happens if all the quantities double between  and
and 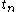 while all the prices stay the same:
while all the prices stay the same:  will double. In either case the change in
will double. In either case the change in  is identical. As such,
is identical. As such,  is as much a quantity index as it is a price index.
is as much a quantity index as it is a price index.Various indices have been constructed in an attempt to compensate for this difficulty.
Paasche and Laspeyres price indices
The two most basic formulae used to calculate price indices are the Paasche index (after the German economist Hermann PaascheHermann Paasche
Hermann Paasche was a German statistician and economist. He is known for his Paasche Index, which provides a calculation of the Price Index. Paasche studied economics, agriculture, statistics and philosophy at University of Halle. In 1879, he became a professor of political science at Aachen...
ˈpaːʃɛ) and the Laspeyres index (after the German economist
Etienne Laspeyres
Étienne Laspeyres
Ernst Louis Étienne Laspeyres was Professor ordinarius of economics and statistics or State Sciences and cameralistics in Basel, Riga, Dorpat , Karlsruhe, and finally for 26 years in Gießen...
lasˈpejres).
The Paasche index is computed as
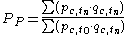
while the Laspeyres index is computed as

where
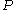 is the relative index of the price levels in two periods,
is the relative index of the price levels in two periods,  is the base period (usually the first year), and
is the base period (usually the first year), and  the period for which the index is computed.
the period for which the index is computed.Note that the only difference in the formulas is that the former uses period n quantities, whereas the latter uses base period (period 0) quantities.
When applied to bundles of individual consumers, a Laspeyres index of 1 would state that an agent in the current period can afford to buy the same bundle as he consumed in the previous period, given that income has not changed; a Paasche index of 1 would state that an agent could have consumed the same bundle in the base period as she is consuming in the current period, given that income has not changed.
Hence, one may think of the Laspeyres index as one where the numeraire
Numéraire
Numéraire is a basic standard by which values are measured. Acting as the numéraire is one of the functions of money, to serve as a unit of account: to measure the worth of different goods and services relative to one another, i.e. in same units...
is the bundle of goods using current year prices but base year quantities. Similarly, the Paasche index can be thought of as a price index taking the bundle of goods using current prices and current quantities as the numeraire.
The Laspeyres index tends to overstate inflation (in a cost of living framework), while the Paasche index tends to understate it, because the indices do not account for the fact that consumers typically react to price changes by changing the quantities that they buy. For example, if prices go up for good
 then, ceteris paribus
then, ceteris paribusCeteris paribus
or is a Latin phrase, literally translated as "with other things the same," or "all other things being equal or held constant." It is an example of an ablative absolute and is commonly rendered in English as "all other things being equal." A prediction, or a statement about causal or logical...
, quantities of that good should go down.
Fisher index and Marshall–Edgeworth index
A third index, the Marshall–Edgeworth index (named for economists Alfred MarshallAlfred Marshall
Alfred Marshall was an Englishman and one of the most influential economists of his time. His book, Principles of Economics , was the dominant economic textbook in England for many years...
and Francis Ysidro Edgeworth
Francis Ysidro Edgeworth
Francis Ysidro Edgeworth FBA was an Irish philosopher and political economist who made significant contributions to the methods of statistics during the 1880s...
), tries to overcome these problems of under- and overstatement by using the arithmetic means of the quantities:
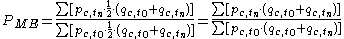
A fourth, the Fisher index (after the American economist Irving Fisher
Irving Fisher
Irving Fisher was an American economist, inventor, and health campaigner, and one of the earliest American neoclassical economists, though his later work on debt deflation often regarded as belonging instead to the Post-Keynesian school.Fisher made important contributions to utility theory and...
), is calculated as the geometric mean
Geometric mean
The geometric mean, in mathematics, is a type of mean or average, which indicates the central tendency or typical value of a set of numbers. It is similar to the arithmetic mean, except that the numbers are multiplied and then the nth root of the resulting product is taken.For instance, the...
of
 and
and  :
: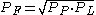
Fisher's index is also known as the “ideal” price index.
However, there is no guarantee with either the Marshall–Edgeworth index or the Fisher index that the overstatement and understatement will exactly cancel the other.
While these indices were introduced to provide overall measurement
Measurement
Measurement is the process or the result of determining the ratio of a physical quantity, such as a length, time, temperature etc., to a unit of measurement, such as the metre, second or degree Celsius...
of relative prices, there is ultimately no way of measuring the imperfections of any of these indices (Paasche, Laspeyres, Fisher, or Marshall–Edgeworth) against reality.
Normalizing index numbers
Price indices are represented as index numbersIndex (economics)
In economics and finance, an index is a statistical measure of changes in a representative group of individual data points. These data may be derived from any number of sources, including company performance, prices, productivity, and employment. Economic indices track economic health from...
, number values that indicate relative change but not absolute values (i.e. one price index value can be compared to another or a base, but the number alone has no meaning). Price indices generally select a base year and make that index value equal to 100. You then express every other year as a percentage of that base year. In our example above, let's take 2000 as our base year. The value of our index will be 100. The price
- 2000: original index value was $2.50; $2.50/$2.50 = 100%, so our new index value is 100
- 2001: original index value was $2.60; $2.60/$2.50 = 104%, so our new index value is 104
- 2002: original index value was $2.70; $2.70/$2.50 = 108%, so our new index value is 108
- 2003: original index value was $2.80; $2.80/$2.50 = 112%, so our new index value is 112
When an index has been normalized in this manner, the meaning of the number 108, for instance, is that the total cost for the basket of goods is 4% more in 2001, 8% more in 2002 and 12% more in 2003 than in the base year (in this case, year 2000).
Relative ease of calculating the Laspeyres index
As can be seen from the definitions above, if one already has price and quantity data (or, alternatively, price and expenditure data) for the base period, then calculating the Laspeyres index for a new period requires only new price data. In contrast, calculating many other indices (e.g., the Paasche index) for a new period requires both new price data and new quantity data (or, alternatively, both new price data and new expenditure data) for each new period. Collecting only new price data is often easier than collecting both new price data and new quantity data, so calculating the Laspeyres index for a new period tends to require less time and effort than calculating these other indices for a new period.Calculating indices from expenditure data
Sometimes, especially for aggregate data, expenditure data is more readily available than quantity data. For these cases, we can formulate the indices in terms of relative prices and base year expenditures, rather than quantities.Here is a reformulation for the Laspeyres index:
Let
 be the total expenditure on good c in the base period, then (by definition) we have
be the total expenditure on good c in the base period, then (by definition) we have
and therefore also
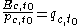 .
.We can substitute these values into our Laspeyres formula as follows:

A similar transformation can be made for any index.
Chained vs non-chained calculations
So far, in our discussion, we have always had our price indices relative to some fixed base period. An alternative is to take the base period for each time period to be the immediately preceding time period. This can be done with any of the above indices, but here's an example with the Laspeyres index, where is the period for which we wish to calculate the index and
is the period for which we wish to calculate the index and  is a reference period that anchors the value of the series:
is a reference period that anchors the value of the series:
Each term

answers the question "by what factor have prices increased between period
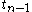 and period
and period  ". When you multiply these all together, you get the answer to the question "by what factor have prices increased since period
". When you multiply these all together, you get the answer to the question "by what factor have prices increased since period  ".
".Nonetheless, note that, when chain indices are in use, the numbers cannot be said to be "in period
 " prices.
" prices.Index number theory
Price index formulas can be evaluated based on their relation to economic concepts (like cost of living) or on their mathematical properties. Several different tests of such properties have been proposed in index number theory literature. W.E. Diewert summarized past research in a list of nine such tests for a price index , where
, where 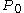 and
and 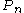 are vectors giving prices for a base period and a reference period while
are vectors giving prices for a base period and a reference period while  and
and  give quantities for these periods.
give quantities for these periods.- Identity test:

- The identity test basically means that if prices remain the same and quantities remain in the same proportion to each other (each quantity of an item is multiplied by the same factor of either
 , for the first period, or
, for the first period, or 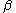 , for the later period) then the index value will be one.
, for the later period) then the index value will be one.
- Proportionality test:

- If each price in the original period increases by a factor α then the index should increase by the factor α.
- Invariance to changes in scale test:
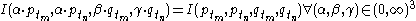
- The price index should not change if the prices in both periods are increased by a factor and the quantities in both periods are increased by another factor. In other words, the magnitude of the values of quantities and prices should not affect the price index.
- Commensurability test:
- The index should not be affected by the choice of units used to measure prices and quantities.
- Symmetric treatment of time (or, in parity measures, symmetric treatment of place):

- Reversing the order of the time periods should produce a reciprocal index value. If the index is calculated from the most recent time period to the earlier time period, it should be the reciprocal of the index found going from the earlier period to the more recent.
- Symmetric treatment of commodities:
- All commodities should have a symmetric effect on the index. Different permutations of the same set of vectors should not change the index.
- Monotonicity test:

- A price index for lower later prices should be lower than a price index with higher later period prices.
- Mean value test:
- The overall price relative implied by the price index should be between the smallest and largest price relatives for all commodities.
- Circularity test:
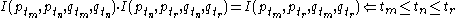
- Given three ordered periods
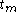 ,
,  ,
,  , the price index for periods
, the price index for periods  and
and  times the price index for periods
times the price index for periods  and
and  should be equivalent to the price index for periods
should be equivalent to the price index for periods  and
and  .
.
Quality change
Price indices often capture changes in price and quantities for goods and services, but they often fail to account for improvements (or often deteriorations) in the quality of goods and services. Statistical agencies generally use matched-model price indices, where one model of a particular good is priced at the same store at regular time intervals. The matched-model method becomes problematic when statistical agencies try to use this method on goods and services with rapid turnover in quality features. For instance, computers rapidly improve and a specific model may quickly become obsolete. Statisticians constructing matched-model price indices must decide how to compare the price of the obsolete item originally used in the index with the new and improved item that replaces it. Statistical agencies use several different methods to make such price comparisons.The problem discussed above can be represented as attempting to bridge the gap between the price for the old item in time t,
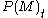 , with the price of the new item in the later time period,
, with the price of the new item in the later time period,  .
.- The overlap method uses prices collected for both items in both time periods, t and t+1. The price relative
 /
/ is used.
is used. - The direct comparison method assumes that the difference in the price of the two items is not due to quality change, so the entire price difference is used in the index.
 /
/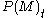 is used as the price relative.
is used as the price relative. - The link-to-show-no-change assumes the opposite of the direct comparison method; it assumes that the entire difference between the two items is due to the change in quality. The price relative based on link-to-show-no-change is 1.
- The deletion method simply leaves the price relative for the changing item out of the price index. This is equivalent to using the average of other price relatives in the index as the price relative for the changing item. Similarly, class mean imputation uses the average price relative for items with similar characteristics (physical, geographic, economic, etc.) to M and N.
See also
- Aggregation problemAggregation problemAn aggregate in economics is a summary measure describing a market or economy. The aggregation problem refers to the difficulty of treating an empirical or theoretical aggregate as if it reacted like a less-aggregated measure, say, about behavior of an individual agent as described in general...
- InflationInflationIn economics, inflation is a rise in the general level of prices of goods and services in an economy over a period of time.When the general price level rises, each unit of currency buys fewer goods and services. Consequently, inflation also reflects an erosion in the purchasing power of money – a...
- GDP deflatorGDP deflatorIn economics, the GDP deflator is a measure of the level of prices of all new, domestically produced, final goods and services in an economy...
- Etienne LaspeyresÉtienne LaspeyresErnst Louis Étienne Laspeyres was Professor ordinarius of economics and statistics or State Sciences and cameralistics in Basel, Riga, Dorpat , Karlsruhe, and finally for 26 years in Gießen...
- Hermann PaascheHermann PaascheHermann Paasche was a German statistician and economist. He is known for his Paasche Index, which provides a calculation of the Price Index. Paasche studied economics, agriculture, statistics and philosophy at University of Halle. In 1879, he became a professor of political science at Aachen...
- Hedonic indexHedonic indexIn econometrics, a hedonic index is any price index which uses information from hedonic regression.Hedonic regression describes how product price could be explained by the product's...
- IndexationIndexationIndexation is a technique to adjust income payments by means of a price index, in order to maintain the purchasing power of the public after inflation....
- Irving FisherIrving FisherIrving Fisher was an American economist, inventor, and health campaigner, and one of the earliest American neoclassical economists, though his later work on debt deflation often regarded as belonging instead to the Post-Keynesian school.Fisher made important contributions to utility theory and...
- Real versus nominal value (economics)
- U.S. Import Price IndexU.S. Import Price IndexThe United States Import Price Index is published by the United States Department of Labor's Bureau of Labor Statistics. It is part of the Office of Prices and Living Conditions. It began as an annual publication, publishing its first index in 1973. It began publishing on a quarterly basis in 1974...
- Volume indexVolume indexA volume index is a numerical time series measure designed to help compare how the production of some class of goods and/or services, taken as a whole, differs between time periods or geographical locations. Compare price index....
Manuals
Data
- PPI data from BLSBureau of Labor StatisticsThe Bureau of Labor Statistics is a unit of the United States Department of Labor. It is the principal fact-finding agency for the U.S. government in the broad field of labor economics and statistics. The BLS is a governmental statistical agency that collects, processes, analyzes, and...

