
Pole and polar
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the terms pole and polar are used to describe a point and a line that have a unique reciprocal relationship with respect to a given conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
. If the point lies on the conic section, its polar is the tangent line to the conic section at that point.
For a given circle, the operation of reciprocation in a circle corresponds to transforming each point in the plane into its polar line and each line in the plane into its pole.
Special case of circles
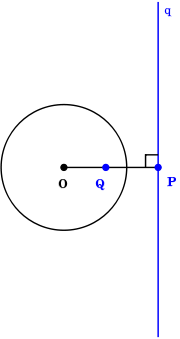
The pole of a line L in a circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
C is a point P that is the inversion in C of the point Q on L that is closest to the center of the circle. Conversely, the polar line (or polar) of a point P in a circle C is the line L such that its closest point Q to the circle is the inversion of P in C.
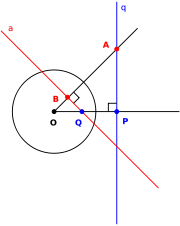
There is another description of the polar line of a point P in the case that it lies outside the circle C. In this case, there are two lines through P which are tangent to the circle
Tangent lines to circles
In Euclidean plane geometry, tangent lines to circles form the subject of several theorems, and play an important role in many geometrical constructions and proofs...
, and the polar of P is the line joining the two points of tangency (not shown here). This shows that pole and polar line are concepts in the projective geometry
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
of the plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
and generalize with any nonsingular conic in the place of the circle C.
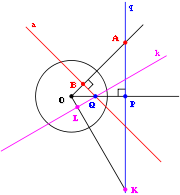
Reciprocation and projective duality
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
. For instance, the polar line can be viewed as the set of projective harmonic conjugates
Projective harmonic conjugates
In projective geometry, the harmonic conjugate point of a triple of points on the real projective line is defined by the following construction due to Karl von Staudt:...
of a given point, the pole, with respect to a conic. The operation of replacing every point by its polar and vice versa is sometimes known as reciprocation.
General conic sections
The concepts of pole, polar and reciprocation can be generalized from circles to other conic sectionConic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
s which are the ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
, hyperbola
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
and parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. This generalization is possible because conic sections result from a reciprocation of a circle in another circle, and the properties involved, such as incidence
Incidence (geometry)
In geometry, the relations of incidence are those such as 'lies on' between points and lines , and 'intersects' . That is, they are the binary relations describing how subsets meet...
and the cross-ratio
Cross-ratio
In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...
, are preserved under all projective transformations.
A general conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
may be written as a second-degree equation in the Cartesian coordinates (x, y) of the plane

where Axx, Axy, Ayy, Bx, By, and C are the constants defining the equation. For such a conic section, the polar line to a given pole point (ξ, η) is defined by the equation
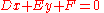
where D, E and F are likewise constants that depend on the pole coordinates (ξ, η)



If the pole lies on the conic section, its polar is tangent to the conic section. However, the pole need not lie on the conic section.
Properties
Poles and polars have several useful properties.If a pole P1 lies on a line L2, then the pole P2 of the line likewise lies on the polar L1.
If a pole P1 moves along a line L2, its polar L1 rotates about the corresponding pole of the line P2, and vice versa.
If two tangent lines can be drawn from a pole to the conic section, then its polar passes through both tangent points.
Applications
Poles and polars were defined by Joseph Diaz GergonneJoseph Diaz Gergonne
Joseph Diaz Gergonne was a French mathematician and logician.-Life:In 1791, Gergonne enlisted in the French army as a captain. That army was undergoing rapid expansion because the French government feared a foreign invasion intended to undo the French Revolution and restore Louis XVI to full power...
and play an important role in his solution of the problem of Apollonius
Problem of Apollonius
In Euclidean plane geometry, Apollonius' problem is to construct circles that are tangent to three given circles in a plane . Apollonius of Perga posed and solved this famous problem in his work ; this work has been lost, but a 4th-century report of his results by Pappus of Alexandria has survived...
.
In planar dynamics a pole is a center of rotation, the polar is the force line of action and the conic is the mass-inertia matrix. The pole-polar relationship is used to define the Center of percussion
Center of percussion
The center of percussion is the point on an object where a perpendicular impact will produce translational and rotational forces which perfectly cancel each other out at some given pivot point, so that the pivot will not be moving momentarily after the impulse....
of a planar rigid body. If the pole is the hinge point, then the polar is the percussion line of action as described in planar Screw theory
Screw theory
Screw theory refers to the algebra and calculus of pairs of vectors, such as forces and moments and angular and linear velocity, that arise in the kinematics and dynamics of rigid bodies....
.
See also
- Dual polygonDual polygonIn geometry, polygons are associated into pairs called duals, where the vertices of one correspond to the edges of the other.-Properties:Regular polygons are self-dual....
- Dual polyhedronDual polyhedronIn geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
- Projective geometryProjective geometryIn mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
- Projective harmonic conjugatesProjective harmonic conjugatesIn projective geometry, the harmonic conjugate point of a triple of points on the real projective line is defined by the following construction due to Karl von Staudt:...
- Polar curvePolar curveIn algebraic geometry, the first polar, or simply polar of an algebraic plane curve C of degree n with respect to a point Q is an algebraic curve of degree n−1 which contains every point of C whose tangent line passes through Q...
External links
- Interactive animation with multiple poles and polars at Cut-the-KnotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...
- Interactive animation with one pole and its polar
- Tutorial at Math-abundance

