In projective geometry

Projective geometry

In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...

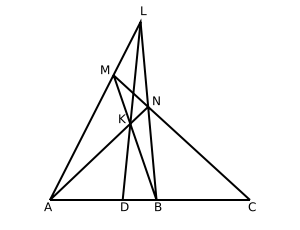
, the harmonic conjugate point of a triple of points on the real projective line is defined by the following construction due to Karl von Staudt:

Given three collinear points A, B, C, let L be a point not lying on their join and let any line through C meet LA, LB at M, N respectively. If AN and BM meet at K, and LK meets AB at D, then D is called the harmonic conjugate of C with respect to A, B.

What is remarkable is that the point D does not depend on what point L is taken initially, nor upon what line through C is used to find M and N. This fact follows from Desargues theorem; it can also be defined in terms of the cross-ratio

Cross-ratio

In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...

 as (A, B; C, D) = −1.

Cross-ratio criterion

The four points are sometimes called a harmonic range on the real projective line. When this line is endowed with the ordinary metric interpretation via real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, then the projective tool of cross-ratio

Cross-ratio

In geometry, the cross-ratio, also called double ratio and anharmonic ratio, is a special number associated with an ordered quadruple of collinear points, particularly points on a projective line...

 is in force. Given this metric context, the harmonic range is characterized by a cross-ratio of minus one:


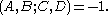
Reordering the points results in the set of three cross-ratios, {−1, 1/2, 2}, which is less than the expected 6 (it is stabilized by exchanging the last 2 points), and is known classically as the harmonic cross-ratio.

The cross-ratio criterion implies that distances from any one of these points to the three remaining points form harmonic progression.

In terms of a double ratio,
given points a and b on an affine line, the division ratio of a point x is
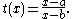
Note that when a < x < b , then t(x) is negative, and that it is positive outside of the interval.
The cross-ratio (c,d;a,b) = t(c)/t(d) is a ratio of division ratios, or a double ratio. Setting the double ratio to minus one means that
when 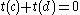, then c and d are projective harmonic conjugates with respect to a and b. So the division ratio criterion is that they be additive inverse

Additive inverse

In mathematics, the additive inverse, or opposite, of a number a is the number that, when added to a, yields zero.The additive inverse of a is denoted −a....

s.

From complete quadrangle

Another approach to the harmonic conjugate is through the concept of a complete quadrangle as expressed by Robin Hartshorne

Robin Hartshorne

Robin Cope Hartshorne is an American mathematician. Hartshorne is an algebraic geometer who studied with Zariski, Mumford, J.-P. Serre and Grothendieck....

 in 1967:

An ordered quadruple of distinct points A,B,C,D on a line is called a harmonic quadruple if there is a complete quadrangle X,Y,Z,W such that A and B are diagonal points of the complete quadrangle (say A = XY.ZW, B = XZ.YW) and C,D lie on the remaining two sides of the quadrangle (say C ∈ XW, D ∈ YZ).

Then Hartshorne shows that assuming Fano's axiom, A,B,C distinct implies there exists a unique D such that A,B,C,D form a harmonic quadruple. In that case he says that D is the "harmonic conjugate of C with respect to A and B".

It was Karl von Staudt that first used the harmonic conjugate as the basis for projective geometry independent of metric considerations:

...Staudt succeeded in freeing projective geometry from elementary geometry. In his Geometrie der Lage Staudt introduced a harmonic quadruple of elements independently of the concept of the cross ratio following a purely projective route, using a complete quadrangle or quadrilateral.

Projective conics

A conic in the projective plane is a curve C that has the following property:
If P is a point not on C, and if a variable line through P meets C at points A and B, then the variable harmonic conjugate of P with respect to A and B traces out a line. The point P is called the pole of that line of harmonic conjugates, and this line is called the polar line of P with respect to the conic. See the article Pole and polar

Pole and polar

In geometry, the terms pole and polar are used to describe a point and a line that have a unique reciprocal relationship with respect to a given conic section...

 for more details.

Inversive geometry

In the case where the conic is a circle, on the extended diameters of the circle, projective hamonic conjugates with respect to the circle are inverses in a circle. This fact follows from one of Smogorzhevsky's theorems:

If circles k and q are mutually orthogonal, then a straight line passing through the center of k and intersecting q, does so at points symmetrical with respect to k.

That is, if the line is an extended diameter of k, then the intersections with q are projective harmonic conjugates.