
Quadric (projective geometry)
Encyclopedia
In projective geometry
a quadric is the set of points of a projective space where a certain quadratic form
on the homogeneous coordinates
becomes zero. It may also be defined as the set of all points that lie on their dual hyperplane
s, under some projective duality of the space.
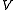 be an
be an 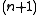 -dimensional vector space
-dimensional vector space
with scalar
field
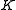 , and let
, and let 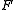 be a quadratic form on
be a quadratic form on 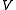 . Let
. Let 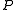 be the
be the  -dimensional projective space corresponding to
-dimensional projective space corresponding to 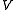 , that is the set
, that is the set 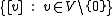 , where
, where 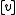 denotes the set of all nonzero multiples of
denotes the set of all nonzero multiples of  . The (projective) quadric defined by
. The (projective) quadric defined by 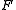 is the set of all points
is the set of all points 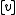 of
of 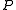 such that
such that  . (This definition is consistent because
. (This definition is consistent because 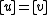 implies
implies 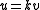 for some
for some 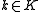 , and
, and 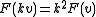 by definition of a quadratic form.)
by definition of a quadratic form.)
When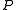 is the real
is the real
or complex projective plane, the quadric is also called a (projective) quadratic curve, conic section, or just conic.
When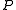 is the real
is the real
or complex projective space
, the quadric is also called a (projective) quadratic surface.
In general, if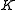 is the field of real numbers, a quadric is an
is the field of real numbers, a quadric is an 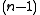 -dimensional sub-manifold
-dimensional sub-manifold
of the projective space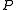 . The exceptions are certain degenerate quadrics that are associated to quadratic forms with special properties. For instance, if
. The exceptions are certain degenerate quadrics that are associated to quadratic forms with special properties. For instance, if 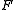 is the trivial or null form (that yields 0 for any vector
is the trivial or null form (that yields 0 for any vector  ), the quadric consists of all points of
), the quadric consists of all points of 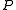 ; if
; if 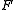 is a definite form
is a definite form
(everywhere positive, or everywhere negative), the quadric is empty; if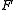 factors into the product of two non-trivial linear forms, the quadric is the union of two hyperplanes; and so on. Some authors may define "quadric" so as to exclude some or all of these special cases.
factors into the product of two non-trivial linear forms, the quadric is the union of two hyperplanes; and so on. Some authors may define "quadric" so as to exclude some or all of these special cases.
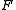 can be expressed as
can be expressed as
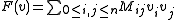
where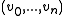 are the coordinates of
are the coordinates of  with respect to some chosen basis, and
with respect to some chosen basis, and 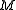 is a certain
is a certain 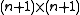 symmetric matrix
symmetric matrix
with entries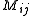 in
in  , that depends on
, that depends on 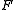 and on the basis.
and on the basis.
This formula can also be written as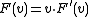 where
where  is the standard inner product of
is the standard inner product of  , and
, and  is the vector of
is the vector of  defined by
defined by
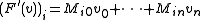
The quadratic form is trivial if and only if all the entries
is trivial if and only if all the entries  are 0. If
are 0. If 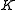 is the real numbers, there is always a basis such that
is the real numbers, there is always a basis such that  is a diagonal matrix
is a diagonal matrix
. In this case, the signs of the diagonal elements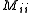 determine whether the quadric is degenerate or not.
determine whether the quadric is degenerate or not.
 defines a projective polarity: a mapping that takes any point
defines a projective polarity: a mapping that takes any point 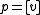 of
of 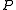 to a hyperplane
to a hyperplane 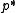 of
of 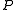 , and vice-versa, while preserving the incidence relation between points and hyperplanes. The coefficient vector of the polar hyperplane
, and vice-versa, while preserving the incidence relation between points and hyperplanes. The coefficient vector of the polar hyperplane 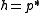 , relative to the chosen basis of
, relative to the chosen basis of 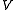 , is
, is 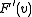 .
.
If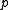 is not on the quadric, the hyperplane
is not on the quadric, the hyperplane 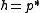 is well-defined (that is, not identically zero) and does not contain
is well-defined (that is, not identically zero) and does not contain 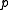 .
.
If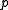 is on the quadric and the hyperplane
is on the quadric and the hyperplane 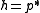 is well-defined, and contains
is well-defined, and contains 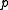 (which is said to be a regular point). In fact, it is the hyperplane that is tangent
(which is said to be a regular point). In fact, it is the hyperplane that is tangent
to the quadric at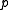 .
.
If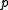 is on the quadric, it may happen that all coefficients
is on the quadric, it may happen that all coefficients 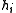 are zero. In that case the polar
are zero. In that case the polar  is not defined, and
is not defined, and  is said to be a singular point or singularity of the quadric.
is said to be a singular point or singularity of the quadric.
The tangent hyperplane turns out to be the union of all lines that are either entirely contained in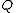 , or intersect
, or intersect 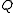 at only one point.
at only one point.
The condition for a point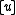 to be in the hyperplane that is tangent to
to be in the hyperplane that is tangent to 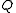 at
at  is
is 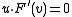 , which is equivalent to
, which is equivalent to 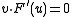
The condition for a point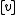 to be singular is
to be singular is 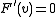 . The quadric has singular points if and only the matrix
. The quadric has singular points if and only the matrix 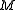 , in diagonal form, has one or more zeros in its diagonal. It follows that the set of all singular points on the quadric is a projective subspace.
, in diagonal form, has one or more zeros in its diagonal. It follows that the set of all singular points on the quadric is a projective subspace.
 at zero, one, or two points, or may be entirely contained in it. The line defined by two distinct points
at zero, one, or two points, or may be entirely contained in it. The line defined by two distinct points 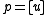 and
and 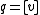 is the set of points of the form
is the set of points of the form 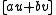 where
where 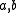 are arbitrary scalars from
are arbitrary scalars from 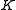 , not both zero. This generic point lies on
, not both zero. This generic point lies on 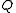 if and only if
if and only if 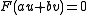 , which is equivalent to
, which is equivalent to
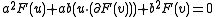
The number of intersections depends on the three coefficients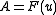 ,
, 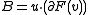 , and
, and 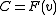 . If all three of
. If all three of 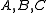 are zero, any pair
are zero, any pair  satisfies the equation, so the line is entirely contained in
satisfies the equation, so the line is entirely contained in 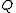 . Otherwise, the line has zero, one, or two distinct intersections depending on whether
. Otherwise, the line has zero, one, or two distinct intersections depending on whether 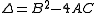 is negative, zero, or positive, respectively.
is negative, zero, or positive, respectively.
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
a quadric is the set of points of a projective space where a certain quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
on the homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
becomes zero. It may also be defined as the set of all points that lie on their dual hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s, under some projective duality of the space.
Formal definition
More formally, let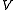 be an
be an 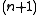 -dimensional vector space
-dimensional vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
with scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
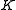 , and let
, and let 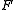 be a quadratic form on
be a quadratic form on 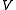 . Let
. Let 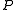 be the
be the  -dimensional projective space corresponding to
-dimensional projective space corresponding to 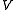 , that is the set
, that is the set 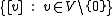 , where
, where 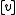 denotes the set of all nonzero multiples of
denotes the set of all nonzero multiples of  . The (projective) quadric defined by
. The (projective) quadric defined by 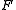 is the set of all points
is the set of all points 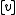 of
of 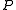 such that
such that  . (This definition is consistent because
. (This definition is consistent because 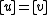 implies
implies 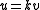 for some
for some 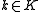 , and
, and 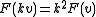 by definition of a quadratic form.)
by definition of a quadratic form.)When
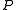 is the real
is the realReal projective plane
In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold, that is, a one-sided surface. It cannot be embedded in our usual three-dimensional space without intersecting itself...
or complex projective plane, the quadric is also called a (projective) quadratic curve, conic section, or just conic.
When
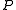 is the real
is the realReal projective space
In mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
or complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, the quadric is also called a (projective) quadratic surface.
In general, if
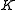 is the field of real numbers, a quadric is an
is the field of real numbers, a quadric is an 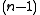 -dimensional sub-manifold
-dimensional sub-manifoldManifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of the projective space
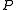 . The exceptions are certain degenerate quadrics that are associated to quadratic forms with special properties. For instance, if
. The exceptions are certain degenerate quadrics that are associated to quadratic forms with special properties. For instance, if 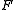 is the trivial or null form (that yields 0 for any vector
is the trivial or null form (that yields 0 for any vector  ), the quadric consists of all points of
), the quadric consists of all points of 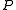 ; if
; if 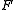 is a definite form
is a definite formDefinite quadratic form
In mathematics, a definite quadratic form is a real-valued quadratic form over some vector space V that has the same sign for every nonzero vector of V...
(everywhere positive, or everywhere negative), the quadric is empty; if
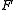 factors into the product of two non-trivial linear forms, the quadric is the union of two hyperplanes; and so on. Some authors may define "quadric" so as to exclude some or all of these special cases.
factors into the product of two non-trivial linear forms, the quadric is the union of two hyperplanes; and so on. Some authors may define "quadric" so as to exclude some or all of these special cases.Matrix representation
Any quadratic form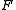 can be expressed as
can be expressed as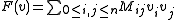
where
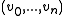 are the coordinates of
are the coordinates of  with respect to some chosen basis, and
with respect to some chosen basis, and 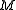 is a certain
is a certain 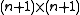 symmetric matrix
symmetric matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
with entries
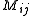 in
in  , that depends on
, that depends on 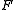 and on the basis.
and on the basis.This formula can also be written as
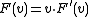 where
where  is the standard inner product of
is the standard inner product of  , and
, and  is the vector of
is the vector of  defined by
defined by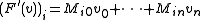
The quadratic form
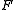 is trivial if and only if all the entries
is trivial if and only if all the entries 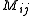 are 0. If
are 0. If 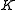 is the real numbers, there is always a basis such that
is the real numbers, there is always a basis such that  is a diagonal matrix
is a diagonal matrixDiagonal matrix
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. The diagonal entries themselves may or may not be zero...
. In this case, the signs of the diagonal elements
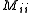 determine whether the quadric is degenerate or not.
determine whether the quadric is degenerate or not.Polarity, tangent hyperplane, and singular points
In general, a projective quadric defines a projective polarity: a mapping that takes any point
defines a projective polarity: a mapping that takes any point 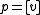 of
of 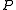 to a hyperplane
to a hyperplane 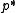 of
of 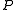 , and vice-versa, while preserving the incidence relation between points and hyperplanes. The coefficient vector of the polar hyperplane
, and vice-versa, while preserving the incidence relation between points and hyperplanes. The coefficient vector of the polar hyperplane 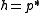 , relative to the chosen basis of
, relative to the chosen basis of 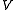 , is
, is 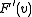 .
.If
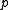 is not on the quadric, the hyperplane
is not on the quadric, the hyperplane 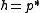 is well-defined (that is, not identically zero) and does not contain
is well-defined (that is, not identically zero) and does not contain 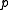 .
.If
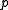 is on the quadric and the hyperplane
is on the quadric and the hyperplane 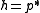 is well-defined, and contains
is well-defined, and contains 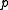 (which is said to be a regular point). In fact, it is the hyperplane that is tangent
(which is said to be a regular point). In fact, it is the hyperplane that is tangentTangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to the quadric at
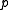 .
.If
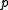 is on the quadric, it may happen that all coefficients
is on the quadric, it may happen that all coefficients 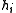 are zero. In that case the polar
are zero. In that case the polar  is not defined, and
is not defined, and  is said to be a singular point or singularity of the quadric.
is said to be a singular point or singularity of the quadric.The tangent hyperplane turns out to be the union of all lines that are either entirely contained in
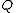 , or intersect
, or intersect 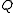 at only one point.
at only one point.The condition for a point
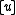 to be in the hyperplane that is tangent to
to be in the hyperplane that is tangent to 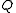 at
at  is
is 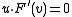 , which is equivalent to
, which is equivalent to 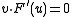
The condition for a point
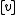 to be singular is
to be singular is 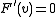 . The quadric has singular points if and only the matrix
. The quadric has singular points if and only the matrix 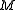 , in diagonal form, has one or more zeros in its diagonal. It follows that the set of all singular points on the quadric is a projective subspace.
, in diagonal form, has one or more zeros in its diagonal. It follows that the set of all singular points on the quadric is a projective subspace.Intersection of lines with quadrics
In projective space, a straight line may intersect a quadric at zero, one, or two points, or may be entirely contained in it. The line defined by two distinct points
at zero, one, or two points, or may be entirely contained in it. The line defined by two distinct points 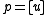 and
and 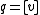 is the set of points of the form
is the set of points of the form 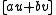 where
where 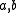 are arbitrary scalars from
are arbitrary scalars from 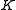 , not both zero. This generic point lies on
, not both zero. This generic point lies on 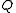 if and only if
if and only if 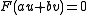 , which is equivalent to
, which is equivalent to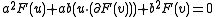
The number of intersections depends on the three coefficients
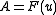 ,
, 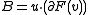 , and
, and 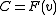 . If all three of
. If all three of 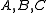 are zero, any pair
are zero, any pair  satisfies the equation, so the line is entirely contained in
satisfies the equation, so the line is entirely contained in 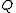 . Otherwise, the line has zero, one, or two distinct intersections depending on whether
. Otherwise, the line has zero, one, or two distinct intersections depending on whether 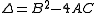 is negative, zero, or positive, respectively.
is negative, zero, or positive, respectively.

