Periodic continued fraction
Encyclopedia
In mathematics
, an infinite periodic continued fraction is a continued fraction
that can be placed in the form
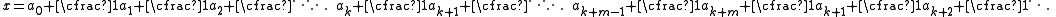
where the initial block of k + 1 partial denominators is followed by a block [ak+1, ak+2,…ak+m] of partial denominators that repeats over and over again, ad infinitum. For example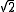
can be expanded to a periodic continued fraction, namely as [1,2,2,2,...].
The partial denominators {ai} can in general be any real or complex numbers. That general case is treated in the article convergence problem. The remainder of this article is devoted to the subject of regular continued fractions
that are also periodic. In other words, the remainder of this article assumes that all the partial denominators ai (i ≥ 1) are positive integers.
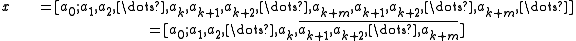
where, in the second line, a vinculum is used to mark the repeating block.
If the initial non-repeating block is not present – that is, if
the regular continued fraction x is said to be purely periodic. For example, the regular continued fraction for the golden ratio
φ – given by [1; 1, 1, 1, …] – is purely periodic, while the regular continued fraction for the square root of two – [1; 2, 2, 2, …] – is periodic, but not purely periodic.
real root of the quadratic equation
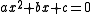
where the coefficients a, b, and c are integers, and the discriminant
, b2 − 4ac, is greater than zero. By the quadratic formula every quadratic irrational can be written in the form
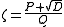
where P, D, and Q are integers, D > 0 is not a perfect square
, and Q divides the quantity P2 − D.
By considering the complete quotient
s of periodic continued fractions, Euler
was able to prove that if x is a regular periodic continued fraction, then x is a quadratic irrational number. The proof is straightforward. From the fraction itself, one can construct the quadratic equation with integral coefficients that x must satisfy.
Lagrange
proved the converse of Euler's theorem: if x is a quadratic irrational, then the regular continued fraction expansion of x is periodic. Given a quadratic irrational x one can construct m different quadratic equations, each with the same discriminant, that relate the successive complete quotients of the regular continued fraction expansion of x to one another. Since there are only finitely many of these equations (the coefficients are bounded), the complete quotients (and also the partial denominators) in the regular continued fraction that represents x must eventually repeat.
is said to be reduced if ζ > 1 and its conjugate
satisfies the inequalities −1 < η < 0. For instance, the golden ratio φ is a reduced surd because its conjugate ½(1 −√5) is greater than −1 and less than zero. On the other hand, the square root of two is not a reduced surd because its conjugate is less than −1.
Galois
proved that the regular continued fraction which represents a quadratic surd ζ is purely periodic if and only if ζ is a reduced surd. In fact, Galois showed more than this. He also proved that if ζ is a reduced quadratic surd and η is its conjugate, then the continued fractions for ζ and for (−1/η) are both purely periodic, and the repeating block in one of those continued fractions is the mirror image of the repeating block in the other. In symbols we have
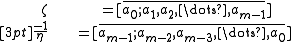
where ζ is any reduced quadratic surd, and η is its conjugate.
From these two theorems of Galois a result already known to Lagrange can easily be deduced. If r > 1 is a rational number that is not a perfect square, then
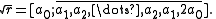
In particular, if n is any non-square positive integer, the regular continued fraction expansion of √n contains a repeating block of length m, in which the first m − 1 partial denominators form a palindromic
string.
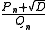
that can possibly arise when ζ = (P + √D)/Q is expanded as a regular continued fraction, Lagrange
showed that the largest partial denominator ai in the expansion is less than 2√D, and that the length of the repeating block is less than 2D.
More recently, sharper arguments based on the divisor function
have shown that L(D), the length of the repeating block for a quadratic surd of discriminant D, is given by
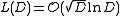
where the big O means "on the order of", or "asymptotically proportional to" (see big O notation
).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an infinite periodic continued fraction is a continued fraction
Generalized continued fraction
In complex analysis, a branch of mathematics, a generalized continued fraction is a generalization of regular continued fractions in canonical form, in which the partial numerators and partial denominators can assume arbitrary real or complex values....
that can be placed in the form
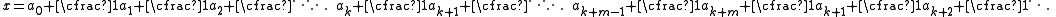
where the initial block of k + 1 partial denominators is followed by a block [ak+1, ak+2,…ak+m] of partial denominators that repeats over and over again, ad infinitum. For example
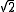can be expanded to a periodic continued fraction, namely as [1,2,2,2,...].The partial denominators {ai} can in general be any real or complex numbers. That general case is treated in the article convergence problem. The remainder of this article is devoted to the subject of regular continued fractions
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
that are also periodic. In other words, the remainder of this article assumes that all the partial denominators ai (i ≥ 1) are positive integers.
Purely periodic and periodic fractions
Since all the partial numerators in a regular continued fraction are equal to unity we can adopt a sort of shorthand in which the continued fraction shown above is written as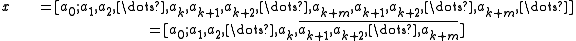where, in the second line, a vinculum is used to mark the repeating block.
If the initial non-repeating block is not present – that is, if
the regular continued fraction x is said to be purely periodic. For example, the regular continued fraction for the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
φ – given by [1; 1, 1, 1, …] – is purely periodic, while the regular continued fraction for the square root of two – [1; 2, 2, 2, …] – is periodic, but not purely periodic.
Relation to quadratic irrationals
A quadratic irrational number is an irrationalIrrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
real root of the quadratic equation
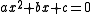
where the coefficients a, b, and c are integers, and the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
, b2 − 4ac, is greater than zero. By the quadratic formula every quadratic irrational can be written in the form
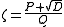
where P, D, and Q are integers, D > 0 is not a perfect square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
, and Q divides the quantity P2 − D.
By considering the complete quotient
Complete quotient
In the metrical theory of regular continued fractions, the kth complete quotient ζ k is obtained by ignoring the first k partial denominators ai...
s of periodic continued fractions, Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
was able to prove that if x is a regular periodic continued fraction, then x is a quadratic irrational number. The proof is straightforward. From the fraction itself, one can construct the quadratic equation with integral coefficients that x must satisfy.
Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
proved the converse of Euler's theorem: if x is a quadratic irrational, then the regular continued fraction expansion of x is periodic. Given a quadratic irrational x one can construct m different quadratic equations, each with the same discriminant, that relate the successive complete quotients of the regular continued fraction expansion of x to one another. Since there are only finitely many of these equations (the coefficients are bounded), the complete quotients (and also the partial denominators) in the regular continued fraction that represents x must eventually repeat.
Reduced surds
The quadratic surd is said to be reduced if ζ > 1 and its conjugateConjugate (algebra)
In algebra, a conjugate of an element in a quadratic extension field of a field K is its image under the unique non-identity automorphism of the extended field that fixes K. If the extension is generated by a square root of an element...
satisfies the inequalities −1 < η < 0. For instance, the golden ratio φ is a reduced surd because its conjugate ½(1 −√5) is greater than −1 and less than zero. On the other hand, the square root of two is not a reduced surd because its conjugate is less than −1.
Galois
Évariste Galois
Évariste Galois was a French mathematician born in Bourg-la-Reine. While still in his teens, he was able to determine a necessary and sufficient condition for a polynomial to be solvable by radicals, thereby solving a long-standing problem...
proved that the regular continued fraction which represents a quadratic surd ζ is purely periodic if and only if ζ is a reduced surd. In fact, Galois showed more than this. He also proved that if ζ is a reduced quadratic surd and η is its conjugate, then the continued fractions for ζ and for (−1/η) are both purely periodic, and the repeating block in one of those continued fractions is the mirror image of the repeating block in the other. In symbols we have
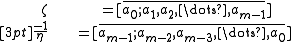
where ζ is any reduced quadratic surd, and η is its conjugate.
From these two theorems of Galois a result already known to Lagrange can easily be deduced. If r > 1 is a rational number that is not a perfect square, then
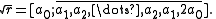
In particular, if n is any non-square positive integer, the regular continued fraction expansion of √n contains a repeating block of length m, in which the first m − 1 partial denominators form a palindromic
Palindrome
A palindrome is a word, phrase, number, or other sequence of units that can be read the same way in either direction, with general allowances for adjustments to punctuation and word dividers....
string.
Length of the repeating block
By analyzing the sequence of combinations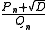that can possibly arise when ζ = (P + √D)/Q is expanded as a regular continued fraction, Lagrange
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
showed that the largest partial denominator ai in the expansion is less than 2√D, and that the length of the repeating block is less than 2D.
More recently, sharper arguments based on the divisor function
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
have shown that L(D), the length of the repeating block for a quadratic surd of discriminant D, is given by
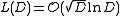
where the big O means "on the order of", or "asymptotically proportional to" (see big O notation
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
).
See also
- Hermite's problemHermite's problemHermite's problem is an open problem in mathematics posed by Charles Hermite in 1848. He asked for a way of expressing real numbers as sequences of natural numbers, such that the sequence is eventually periodic precisely when the original number is a cubic irrational.-Motivation:A standard way of...
- Methods of computing square roots#Continued fraction expansion
- Restricted partial quotients