Restricted partial quotients
Encyclopedia
In mathematics
, and more particularly in the analytic theory of regular continued fractions
, an infinite regular continued fraction x is said to be restricted, or composed of restricted partial quotients, if the sequence of denominators of its partial quotients is bounded; that is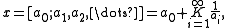
and there is some positive integer M such that all the (integral) partial denominators ai are less than or equal to M.
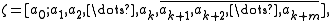
then ζ is a quadratic irrational
number, and its representation as a regular continued fraction is periodic. Clearly any regular periodic continued fraction consists of restricted partial quotients, since none of the partial denominators can be greater than the largest of a0 through ak+m. Historically, mathematicians studied periodic continued fractions before considering the more general concept of restricted partial quotients.
is a set C of measure zero from which a complete interval
of real numbers can be constructed by simple addition – that is, any real number from the interval can be expressed as the sum of exactly two elements of the set C. The usual proof of the existence of the Cantor set is based on the idea of punching a "hole" in the middle of an interval, then punching holes in the remaining sub-intervals, and repeating this process ad infinitum.
The process of adding one more partial quotient to a finite continued fraction is in many ways analogous to this process of "punching a hole" in an interval of real numbers. The size of the "hole" is inversely proportional to the next partial denominator chosen – if the next partial denominator is 1, the gap between successive convergent
s is maximized.
To make the following theorems precise we will consider CF(M), the set of restricted continued fractions whose values lie in the open interval (0, 1) and whose partial denominators are bounded by a positive integer M – that is,
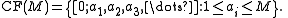
By making an argument parallel to the one used to construct the Cantor set two interesting results can be obtained.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, and more particularly in the analytic theory of regular continued fractions
Continued fraction
In mathematics, a continued fraction is an expression obtained through an iterative process of representing a number as the sum of its integer part and the reciprocal of another number, then writing this other number as the sum of its integer part and another reciprocal, and so on...
, an infinite regular continued fraction x is said to be restricted, or composed of restricted partial quotients, if the sequence of denominators of its partial quotients is bounded; that is
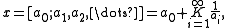
and there is some positive integer M such that all the (integral) partial denominators ai are less than or equal to M.
Periodic continued fractions
A regular periodic continued fraction consists of a finite initial block of partial denominators followed by a repeating block; if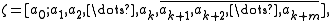then ζ is a quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
number, and its representation as a regular continued fraction is periodic. Clearly any regular periodic continued fraction consists of restricted partial quotients, since none of the partial denominators can be greater than the largest of a0 through ak+m. Historically, mathematicians studied periodic continued fractions before considering the more general concept of restricted partial quotients.
Restricted CFs and the Cantor set
The Cantor setCantor set
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of remarkable and deep properties. It was discovered in 1875 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883....
is a set C of measure zero from which a complete interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
of real numbers can be constructed by simple addition – that is, any real number from the interval can be expressed as the sum of exactly two elements of the set C. The usual proof of the existence of the Cantor set is based on the idea of punching a "hole" in the middle of an interval, then punching holes in the remaining sub-intervals, and repeating this process ad infinitum.
The process of adding one more partial quotient to a finite continued fraction is in many ways analogous to this process of "punching a hole" in an interval of real numbers. The size of the "hole" is inversely proportional to the next partial denominator chosen – if the next partial denominator is 1, the gap between successive convergent
Convergent (continued fraction)
A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction The nth convergent is also known as the nth approximant of a continued fraction.-Representation of real numbers:...
s is maximized.
To make the following theorems precise we will consider CF(M), the set of restricted continued fractions whose values lie in the open interval (0, 1) and whose partial denominators are bounded by a positive integer M – that is,
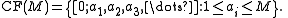
By making an argument parallel to the one used to construct the Cantor set two interesting results can be obtained.
- If M ≥ 4, then any real number in an interval can be constructed as the sum of two elements from CF(M), where the interval is given by
-
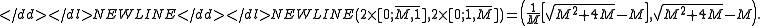
- A simple argument shows that
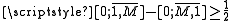holds when M ≥ 4, and this in turn implies that if M ≥ 4, every real number can be represented in the form n + CF1 + CF2, where n is an integer, and CF1 and CF2 are elements of CF(M).
- A simple argument shows that