
Perfect space
Encyclopedia
In mathematics
, in the field of topology
, perfect spaces are spaces that have no isolated point
s. In such spaces, every point can be approximated arbitrarily well by other points - given any point and any topological neighborhood of the point, there is another point within the neighborhood.
The term perfect space is also used, incompatibly, to refer to other properties of a topological space, such as being a Gδ space
. Context is required to determine which meaning is intended.
In this article, a space which is not perfect will be referred to as imperfect.
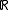 is a connected perfect space, while the Cantor space
is a connected perfect space, while the Cantor space
2ω and Baire space
ωω are perfect, totally disconnected zero dimensional
spaces.
Any nonempty set admits an imperfect topology: the discrete topology. Any set with more
than one point admits a perfect topology: the indiscrete topology.
is a cardinal invariant -- i.e., a mapping which assigns to each topological space a cardinal number
such that homeomorphic spaces get assigned the same number.
A space is perfect if and only if it has imperfection zero.
Perfection is a local property of a topological space: a space is perfect if and only if every
point in the space admits a basis of neighborhoods each of which is perfect in the subspace topology.
Let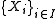 be a family of topological spaces.
be a family of topological spaces.
As for any local property, the disjoint union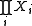 is perfect if and only if each
is perfect if and only if each 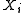 is perfect.
is perfect.
The Cartesian product of a family is perfect in the product topology
is perfect in the product topology
if and only if at least one of the following holds:
(i) At least one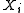 is perfect.
is perfect.
(ii)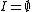 .
.
(iii) The set of indices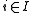 such that
such that 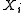 has at least two points is infinite.
has at least two points is infinite.
A continuous image, and even a quotient, of a perfect space need not be perfect. For example, let X = R-{0}, let Y = {1, 2} given the discrete topology and let f be a function defined such that f(x) = 2 if x > 0 and f(x) = 1 if x < 0. However, every image of a perfect space under an injective continuous map is perfect.
to that of a T1 space
-- in which every singleton set is closed.
A T1 space is perfect if and only if every point of the space is an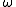 -accumulation point
-accumulation point
. In particular a nonempty perfect T1 space is infinite.
Any connected
T1 space with more than one point is perfect. (More interesting therefore are disconnected perfect spaces, especially totally disconnected perfect spaces like Cantor space and Baire space.)
On the other hand, the set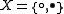 endowed with the topology
endowed with the topology 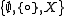 is connected, T0 (and even sober
is connected, T0 (and even sober
) but not perfect (this space is called Sierpinski space
).
Suppose X is a homogeneous topological space, i.e., the group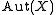 of self-homeomorphisms acts transitively on X. Then X is either perfect or
of self-homeomorphisms acts transitively on X. Then X is either perfect or
discrete. This holds in particular for all topological groups.
A space which is of the first category is necessarily perfect (so, similar to compactifiying a space, we can 'make' a space to be of the second category by taking the disjoint union with a one-point space).
establish limits on the cardinality of non-empty, perfect spaces with additional completeness properties. These results show that:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, perfect spaces are spaces that have no isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s. In such spaces, every point can be approximated arbitrarily well by other points - given any point and any topological neighborhood of the point, there is another point within the neighborhood.
The term perfect space is also used, incompatibly, to refer to other properties of a topological space, such as being a Gδ space
G-delta space
In mathematics, particularly topology, a Gδ space a space in which closed sets are ‘separated’ from their complements using only countably many open sets. A Gδ space may thus be regarded as a space satisfying a different kind of separation axiom...
. Context is required to determine which meaning is intended.
In this article, a space which is not perfect will be referred to as imperfect.
Examples and nonexamples
The real line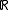 is a connected perfect space, while the Cantor space
is a connected perfect space, while the Cantor spaceCantor space
In mathematics, a Cantor space, named for Georg Cantor, is a topological abstraction of the classical Cantor set: a topological space is a Cantor space if it is homeomorphic to the Cantor set. In set theory, the topological space 2ω is called "the" Cantor space...
2ω and Baire space
Baire space
In mathematics, a Baire space is a topological space which, intuitively speaking, is very large and has "enough" points for certain limit processes. It is named in honor of René-Louis Baire who introduced the concept.- Motivation :...
ωω are perfect, totally disconnected zero dimensional
Zero-dimensional space
In mathematics, a zero-dimensional topological space is a topological space that has dimension zero with respect to one of several inequivalent notions of assigning a dimension to a given topological space...
spaces.
Any nonempty set admits an imperfect topology: the discrete topology. Any set with more
than one point admits a perfect topology: the indiscrete topology.
Imperfection of a space
Define the imperfection of a topological space to be the number of isolated points. Thisis a cardinal invariant -- i.e., a mapping which assigns to each topological space a cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
such that homeomorphic spaces get assigned the same number.
A space is perfect if and only if it has imperfection zero.
Closure properties
Every nonempty perfect space has subsets which are imperfect in the subspace topology, namely the singleton sets. However, any open subspace of a perfect space is perfect.Perfection is a local property of a topological space: a space is perfect if and only if every
point in the space admits a basis of neighborhoods each of which is perfect in the subspace topology.
Let
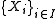 be a family of topological spaces.
be a family of topological spaces.As for any local property, the disjoint union
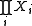 is perfect if and only if each
is perfect if and only if each 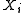 is perfect.
is perfect.The Cartesian product of a family
 is perfect in the product topology
is perfect in the product topologyProduct topology
In topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
if and only if at least one of the following holds:
(i) At least one
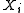 is perfect.
is perfect.(ii)
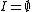 .
.(iii) The set of indices
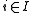 such that
such that 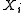 has at least two points is infinite.
has at least two points is infinite.A continuous image, and even a quotient, of a perfect space need not be perfect. For example, let X = R-{0}, let Y = {1, 2} given the discrete topology and let f be a function defined such that f(x) = 2 if x > 0 and f(x) = 1 if x < 0. However, every image of a perfect space under an injective continuous map is perfect.
Connection with other topological properties
It is natural to compare the concept of a perfect space -- in which no singleton set is open --to that of a T1 space
T1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
-- in which every singleton set is closed.
A T1 space is perfect if and only if every point of the space is an
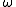 -accumulation point
-accumulation pointLimit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
. In particular a nonempty perfect T1 space is infinite.
Any connected
Connected space
In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
T1 space with more than one point is perfect. (More interesting therefore are disconnected perfect spaces, especially totally disconnected perfect spaces like Cantor space and Baire space.)
On the other hand, the set
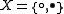 endowed with the topology
endowed with the topology 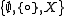 is connected, T0 (and even sober
is connected, T0 (and even soberSober space
In mathematics, a sober space is a topological spacesuch that every irreducible closed subset of X is the closure of exactly one point of X: that is, has a unique generic point.-Properties and examples :...
) but not perfect (this space is called Sierpinski space
Sierpinski space
In mathematics, the Sierpiński space is a finite topological space with two points, only one of which is closed.It is the smallest example of a topological space which is neither trivial nor discrete...
).
Suppose X is a homogeneous topological space, i.e., the group
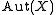 of self-homeomorphisms acts transitively on X. Then X is either perfect or
of self-homeomorphisms acts transitively on X. Then X is either perfect ordiscrete. This holds in particular for all topological groups.
A space which is of the first category is necessarily perfect (so, similar to compactifiying a space, we can 'make' a space to be of the second category by taking the disjoint union with a one-point space).
Perfect spaces in descriptive set theory
Classical results in descriptive set theoryDescriptive set theory
In mathematical logic, descriptive set theory is the study of certain classes of "well-behaved" subsets of the real line and other Polish spaces...
establish limits on the cardinality of non-empty, perfect spaces with additional completeness properties. These results show that:
- If X is a complete metric space with no isolated points, then the Cantor space 2ω can be continuously embedded into X. Thus X has cardinality at least
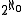 . If X is a separable, complete metric space with no isolated points, the cardinality of X is exactly
. If X is a separable, complete metric space with no isolated points, the cardinality of X is exactly 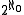 .
. - If X is a locally compact Hausdorff space with no isolated points, there is an injective function (not necessarily continuous) from Cantor space to X, and so X has cardinality at least
 .
.
See also
- Dense-in-itselfDense-in-itselfIn mathematics, a subset A of a topological space is said to be dense-in-itself if A contains no isolated points.Every dense-in-itself closed set is perfect. Conversely, every perfect set is dense-in-itself....
- Finite intersection propertyFinite intersection propertyIn general topology, a branch of mathematics, the finite intersection property is a property of a collection of subsets of a set X. A collection has this property if the intersection over any finite subcollection of the collection is nonempty....
- Derived set (mathematics)Derived set (mathematics)In mathematics, more specifically in point-set topology, the derived set of a subset S of a topological space is the set of all limit points of S...
- Subspace topologySubspace topologyIn topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...

