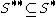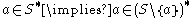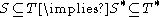Derived set (mathematics)
Encyclopedia
In mathematics
, more specifically in point-set topology, the derived set of a subset S of a topological space
is the set of all limit point
s of S. It is usually denoted by S′.
The concept was first introduced by Georg Cantor
in 1872 and he developed set theory
in large part to study derived sets on the real line
.
is closed
precisely when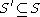 . Two subsets S and T are separated
. Two subsets S and T are separated
precisely when they are disjoint and each is disjoint from the other's derived set (though the derived sets don't need to be disjoint from each other).
The set S is defined to be a perfect set if S = S′. Equivalently, a perfect set is a closed set with no isolated point
s. Perfect sets are particularly important in applications of the Baire category theorem
.
Two topological spaces are homeomorphic if and only if there is a bijection
from one to the other such that the derived set of the image of any subset is the image of the derived set of that subset.
The Cantor–Bendixson theorem states that any Polish space
can be written as the union of a countable set and a perfect set. Because any Gδ
subset of a Polish space is again a Polish space, the theorem also shows that any Gδ subset of a Polish space is the union of a countable set and a set that is perfect with respect to the induced topology
.
. A set of points X can be equipped with an operator * mapping subsets of X to subsets of X, such that for any set S and any point a:
Note that given 5, 3 is equivalent to 3' below, and that 4 and 5 together are equivalent to 4' below, so we have the following equivalent axioms:
Calling a set S closed if will define a topology on the space in which * is the derived set operator, that is,
will define a topology on the space in which * is the derived set operator, that is, 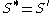 . If we also require that the derived set of a set consisting of a single element be empty, the resulting space will be a T1 space
. If we also require that the derived set of a set consisting of a single element be empty, the resulting space will be a T1 space
.
s α, the α-th Cantor–Bendixson derivative of a topological space is defined by transfinite induction
as follows:
The transfinite sequence of Cantor–Bendixson derivatives of X must eventually be constant. The smallest ordinal α such that Xα+1 = Xα is called the Cantor–Bendixson rank of X.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in point-set topology, the derived set of a subset S of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is the set of all limit point
Limit point
In mathematics, a limit point of a set S in a topological space X is a point x in X that can be "approximated" by points of S in the sense that every neighbourhood of x with respect to the topology on X also contains a point of S other than x itself. Note that x does not have to be an element of S...
s of S. It is usually denoted by S′.
The concept was first introduced by Georg Cantor
Georg Cantor
Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...
in 1872 and he developed set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
in large part to study derived sets on the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
.
Properties
A subset S of a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
is closed
Closed set
In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
precisely when
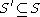 . Two subsets S and T are separated
. Two subsets S and T are separatedSeparated sets
In topology and related branches of mathematics, separated sets are pairs of subsets of a given topological space that are related to each other in a certain way....
precisely when they are disjoint and each is disjoint from the other's derived set (though the derived sets don't need to be disjoint from each other).
The set S is defined to be a perfect set if S = S′. Equivalently, a perfect set is a closed set with no isolated point
Isolated point
In topology, a branch of mathematics, a point x of a set S is called an isolated point of S, if there exists a neighborhood of x not containing other points of S.In particular, in a Euclidean space ,...
s. Perfect sets are particularly important in applications of the Baire category theorem
Baire category theorem
The Baire category theorem is an important tool in general topology and functional analysis. The theorem has two forms, each of which gives sufficient conditions for a topological space to be a Baire space....
.
Two topological spaces are homeomorphic if and only if there is a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
from one to the other such that the derived set of the image of any subset is the image of the derived set of that subset.
The Cantor–Bendixson theorem states that any Polish space
Polish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
can be written as the union of a countable set and a perfect set. Because any Gδ
G-delta set
In the mathematical field of topology, a Gδ set is a subset of a topological space that is a countable intersection of open sets. The notation originated in Germany with G for Gebiet meaning open set in this case and δ for Durchschnitt .The term inner limiting set is also used...
subset of a Polish space is again a Polish space, the theorem also shows that any Gδ subset of a Polish space is the union of a countable set and a set that is perfect with respect to the induced topology
Induced topology
In topology and related areas of mathematics, an induced topology on a topological space is a topology which is "optimal" for some function from/to this topological space.- Definition :Let X_0, X_1 be sets, f:X_0\to X_1....
.
Topology in terms of derived sets
Because homeomorphisms can be described entirely in terms of derived sets, derived sets have been used as the primitive notion in topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
. A set of points X can be equipped with an operator * mapping subsets of X to subsets of X, such that for any set S and any point a:
Note that given 5, 3 is equivalent to 3' below, and that 4 and 5 together are equivalent to 4' below, so we have the following equivalent axioms:
-
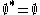
-
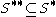
- 3'.
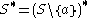
- 4'.
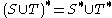
- 3'.
Calling a set S closed if
 will define a topology on the space in which * is the derived set operator, that is,
will define a topology on the space in which * is the derived set operator, that is, 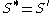 . If we also require that the derived set of a set consisting of a single element be empty, the resulting space will be a T1 space
. If we also require that the derived set of a set consisting of a single element be empty, the resulting space will be a T1 spaceT1 space
In topology and related branches of mathematics, a T1 space is a topological space in which, for every pair of distinct points, each has an open neighborhood not containing the other. An R0 space is one in which this holds for every pair of topologically distinguishable points...
.
Cantor–Bendixson rank
For ordinal numberOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s α, the α-th Cantor–Bendixson derivative of a topological space is defined by transfinite induction
Transfinite induction
Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...
as follows:
- X0 = X
- Xα+1 = (Xα)'
- Xλ =
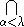 Xα for limit ordinals λ.
Xα for limit ordinals λ.
The transfinite sequence of Cantor–Bendixson derivatives of X must eventually be constant. The smallest ordinal α such that Xα+1 = Xα is called the Cantor–Bendixson rank of X.